Устойчивость сжатых стержней. Продольный изгиб

Разрушение стержня может произойти не только потому, что будет нарушена прочность, но и оттого, что стержень не сохранит заданной формы. Например, изгиб при продольном сжатии тонкой линейки. Потеря устойчивости прямолинейной формы равновесия центрально сжатого стержня называетсяпродольным изгибом. Упругое равновесиеустойчиво, если деформированное тело при любом малом отклонении от состояния равновесия стремится вернуться к первоначальному состоянию и возвращается к нему при удалении внешнего воздействия. Нагрузка, превышение которой вызывает потерю устойчивости, называетсякритической нагрузкойР_кр(критической силой). Допускаема нагрузка [P]=P_кр/n_у,n_у– нормативный коэффициент запаса устойчивости. Приближенное дифференциальное ур-ние упругой линии:, Е –модуль упругости материала стержня, М – изгибающий момент,J_min– наименьший момент инерции сечения стержня. При потере устойчивости прогиб, как правило, происходит перпендикулярно к оси наименьшей жесткости, относительно которой —J=J_min. Рассматривается приближенное дифф-ное ур-ие, т.к. потеря устойчивости возникает при малых деформациях.M=—Py, получаем однородное дифф-ное уравнение:, где. Решая дифф-ное ур-ие находим наименьшее значение критической силы –формула Эйлера:– формула дает значение критической силы для стержня с шарнирно закрепленными концами. При различных закреплениях:,– коэффициент приведения длины. При шарнирном закреплении обоих концов стержня=1; для стержня с заделанными концами=0,5; для стержня с одним заделанным и другим свободным концом=2; для стержня с одним заделанным и другим шарнирно закрепленным концом=0,7.

Критическое сжимающее напр-ние.: ,– гибкость стержня, – наименьший главный радиус инерции площади сечения стержня. Эти формулы справедливы только тогда, когда напряжения_кр_пц– предел пропорциональности, т.е. в пределах применимости закона Гука. Формула Эйлера применима при гибкости стержня:, например, для стали Ст3 (С235)_кр100. Для случая<_кркритическое напряжение вычисляется по эмпирической (полученной экспериментально)формуле Ясинского:_кр=a—b, коэффициенты "a" и "b" в справочной лит-ре (Ст3:a=310МПа;b=1,14МПа).

Достаточно короткие стержни, для которых <₀=40 (для сталей) назыв-тся стержни малой гибкости. Такие стержни рассчитывают только на прочность, т.е. принимают_кр=_т(предел текучести) – для пластичных материалов и_кр=_В(временное сопротивление) – для хрупких материалов. При расчете стержней большой гибкости используют условие устойчивости:,F_брутто– полная площадь сечения,

(F_нетто=F_брутто—F_ослабл–площадь ослабленного сечения с учетом площади отверстий в сеченииF_ослабл, например, от заклепок). [_у]=_кр/n_у,n_у– нормативный коэф. запаса устойчивости. Допускаемое напряжение [_у] выражается через основное допускаемое напряжение [], используемое при расчетах на прочность: [_у]=[],–коэффициент уменьшения допускаемого напряжениядля сжатых стержней (коэффициент продольного изгиба). Значенияприведены в табл. в учебниках и зависят от материала стержня и его гибкости (например, для стали Ст3 при=120=0,45).

При проектировочном расчете требуемой площади сечения на первом шаге принимают ₁=0,5–0,6; находят:. Далее знаяF_брутто, подбирают сечение, определяютJ_min,i_minи, устанавливают по табл. фактическое₁^I, если оно существенно отличается от₁, расчет повторяется при среднем₂= (₁+₁^I)/2. В результате второй попытки находят₂^I, сравнивают с предыдущем значением и т.д., пока не достигнуто достаточно близкое совпадение. Обычно требуется 2-3 попытки.

Формулы

Нормальное напряжение: ; относительная деформация ; Закон Гука: ;  = Е; ; абсолют. удлинение ; относит. поперечная деформация ; коэфф.Пуассона ; удлинение стержня ; работа при растяжении ; потенциальная энергия; учет собств. веса стержня:N(z) = P + FL; ; ; условие прочности при растяж.-сж: _max []; – допуск. напр.;линейное напряженное состояние: полное напр.: ; нормальное: ; касательное:

; на перпендикулярных площадках ;;

_= — _; главные напряжения: ₁>₂>₃; на наклонной площадке: ;или; закон парности касательных напр._xz= — _zx; ; ; ;;;_+_=₁+₂; макс. касательное напряжение ; главные напр-ния ;

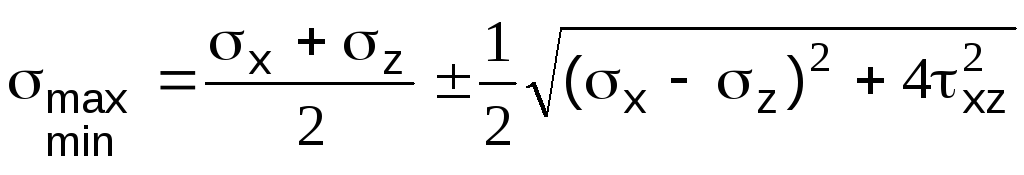положение главных площадок ; ;

объемное напряженное состояние: ;

;макс.касат.напр.;

напряжения по октаэдрической площадке ;

; ;

интенсивность напряжений ;

первый инвариант: _x+_y+_z=₁+₂+₃; обобщенный закон Гука:

;

относит. объемная деформация ;;

среднее напряжение ;;модуль объемной деформации: К=; потенц.энергия U=; удельная потенциальная энергия

u = ; ; ;

; u = u_о + u_ф; энергия из-за изменения объема: ; энергия из-за изменения формы:

; тензор напряжений:

; тензор для главных напряжений:

Инварианты напряженного состояния:

J₁= _x + _y + _z; J₂= _x_y +_y_z + _y_z — ²_xy — ²_zx — ²_yz;

J₃= _x_y_z — _x²_yz — _y²_zx — _z²_xy + 2_xy_zx_yz.

Сопоставление зависимостей напряженного и деформированного плоского сост.:

; ;

; ;Инварианты деформированного состояния:

J₁= _x + _y + _z; J₂= _x_y +_y_z + _z_x — ²_xy — ²_yz — ²_zx;

тензор деформаций:; .

1-ая теория прочности (теория наибольших нормальных напряжений):_max= ₁ [].

2-ая теор. прочности (теория наибольших относительных деформаций): _max= ₁ []. ₁=, условие прочности _эквII= ₁ — (₂ + ₃) [].

3-я теор. проч. (теория наибольших касательных напряжений):_max  [], _max=,

условие прочности: _эквIII= ₁ — ₃ [], _эквIII=  []. При _y=0 . 4-я теор. прочности (энергетическая теория):

u_ф[u_ф]. . Для плоского напряж. сост.:._y=0,  .

Теория прочности Мора:, когда допускаемые напряжения на растяжение [_p] и сжатие [_с] не одинаковы (чугун).

Чистый сдвиг. ; угол сдвига  . Закон Гука при сдвиге: = /G;  = G;

модуль сдвига (модуль второго рода): ; потенциальная энергия при сдвиге ; удельная потенц. энергия: ; объемV=аF; ;

Геометрические характеристики сечений: площадь ; статический момент относительно осиx или y: ; ; координаты центра тяжести:

; ;;

Осевой момент инерции: ; ; полярный момент инер.: ;

J_y + J_x = J_p; центробежный момент инерции: . Прямоугольник:

; J_xy=0. Круг: .Четверть круга: J_y=J_x=0,055R⁴; J_xy=0,0165R⁴; J_x0=0,0714R⁴; J_y0=0,0384R⁴. Моменты инерции относительно параллельных осей: J_x1=J_x + a²F; J_y1=J_y + b²F; J_y1x1=J_yx + abF. Моменты инерции при повороте осей: J_x1=J_xcos² + J_ysin² — J_xysin2; J_y1=J_ycos² + J_xsin² + J_xysin2; J_x1y1=(J_x — J_y)sin2 + J_xycos2; J_y1 + J_x1= J_y + J_x. Угол, определяющий положение главных осей: . Мом-ты инерц. относит. главн. центр. осей инерц.:;J_max+J_min=J_x+J_y.

Радиус инерции: ;J_x=Fi_x², J_y=Fi_y². Осевой момент сопротивления:

; для прямоугольника: ; для круга:

W_x=W_y= ; трубчатое сечение (кольцо): W_x=W_y= ;

 = d_Н/d_B. Полярный момент сопротивления: ; для круга:W_р= .

Кручение. ,. Угол закручивания:; относит. угол закручивания:. Потенциальная энергия при кручении:;

Условие прочности: ; [] =; условие жесткости: _mкax[]. Кручение бруса прямоугольного сеч.: ;;W_k= hb²; J_k= hb³; = _max.

Изгиб. . Нормальные напряжения: . Закон Гука при изгибе:, формула Навье:. Максимальные напряжения:

, J_x/y_max=W_x—момент сопротивления сечения при изгибе, .

Касательные напряжения – формула Журавского: . Для прямоугольного сечения:,F=bh, для круглого сечения:,F=R², для любого сечения: . Главные напряжения при поперечном изгибе:.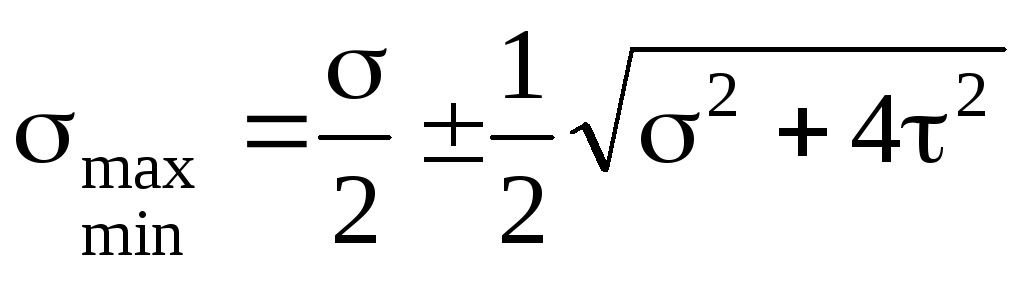

Условие прочности по нормальным напряжениям , условие прочности по касательным напряжениям.

Условия прочности по различным теориям прочн.: I-я: ;

II-я:(при коэфф.Пуассона=0,3);

III-я:,IV-я:,

теория Мора: ,.

Закон Гука при изгибе: .— дифференциальное уравнение изогнутой оси балки. Приближенноедифференциальное уравнение изогнутой оси балки: .— уравнение углов поворота,— уравнение прогибов. Метод начальных параметров.

EJ=M(x) = R_Ax – – M(x – a)⁰ + – P(x – a – b); интегрируем:

EJ = EJ₀ + R_A–– M(x – a) +– P;

EJy =EJy₀ + EJ₀x + R_A–– M+– P.

Дифференциальные зависимости при изгибе: ;;

; . Определение перемещений способом фиктивной нагрузки.

; ;;;. Теорема о трех моментах:

.

Косой изгиб. Напряжение в произв. точке с координатами "x,y": ;

, M_x=Mcos; M_y=Msin, . Уравнение нейтр. линии:

, или .Угол наклона нейтральной линии к главной оси "х":.. Наиб. напр.,

W_x=J_x/y_max; W_y=J_y/x_max. Прогиб "f": , .

Внецентренное сжатие–растяжение. Нормальное напряжение в произвольной точке:

; N>0 – если сила растягивающая, M_x, M_y>0, если моменты "растягивают" сеч. в I-ой четверти. Внутренние усилия: N=P; M_y=Px_p; M_x=Py_p. Напряжения: или ,

Уравнение нейтр. линии: . Отрезки, отсекаемые нейтр. линией на осях коорд.: . – координаты контура ядра.

Изгиб с кручением. Макс. нормальные и касательные напряжения в опасных точках:

, , (для круга:W=–осевой момент сопротивления, W_р= –полярный момент сопротивления сечения). Главные напряжения в опасных точках:

Проверка прочности: по IV-ой теории прочности:

теория Мора: m=[_p]/[_c].

.

Приведенный момент: ;

I-ая теория:

II-ая: , при коэффициент Пуассона=0,3;

III-я: IV-ая: ;

, момент сопротивления: , диаметр вала:.

Перемещение, вызванное несколькими силовыми факторами: _Р=_РP+_РQ+_РM. Перемещение вызванное силой Р, будет: _Р=Р_Р. Работа внешних сил, действующих на упругую систему: .– работа при статическом действии обобщенной силы на упругую систему.

Работа внутренних сил (сил упругости) в случае плоского изгиба: . Потенциальная энергияU=A.

Теорема о взаимности работ (теорема Бетли): А₁₂=А₂₁, Р₁₁₂=Р₂₂₁.

₁₁– перемещение по направлению силы Р₁ от действия силы Р₁;

₁₂– перемещение по направлению силы Р₁ от действия силы Р₂;

₂₁– перемещение по направлению силы Р₂ от действия силы Р₁;

₂₂– перемещение по направлению силы Р₂ от действия силы Р₂.

А₁₂=Р₁₁₂ – работа силы Р₁ первого состояния на перемещении по ее направлению, вызванном силой Р₂ второго состояния. Аналогично: А₂₁=Р₂₂₁ – работа силы Р₂ второго состояния на перемещении по ее направлению, вызванном силой Р₁ первого состояния..

Т

еорема о взаимности перемещений (теорема Максвелла) Если Р₁=1 и Р₂=1, то Р₁₁₂=Р₂₂₁, т.е. ₁₂=₂₁, в общем случае _mn=_nm. Обобщенное перемещение (формула или интеграл Мора):

Для плоской системы: ..

Вычисление интегр. Мора способом Верещагина. ..

Перемножение эпюр, имеющих вид трапеций: .

П

₁₁Х₁+₁₂Х₂+…+_1nХ_n+_1p=0

₂₁Х₁+₂₂Х₂+…+_2nХ_n+_2p=0

. . . . . . . . . . . .

_n1Х₁+_n2Х₂+…+_nnХ_n+_np=0

ри действии равномерно распределенной нагрузки на шарнирно опертую балку эпюра строится в виде выпуклой квадратичной параболы, площадь,, т.е., х_С=L/2. Для "глухой" заделки при равномерно распределенной нагрузке имеем вогнутую квадратичную параболу, для которой ;,, х_С=3L/4. Теорема Кастильяно: ,,.

Канонические уравнения метода сил:

; ; ….;;

; ; ….;;

; ; ….;,

коэффициенты находят по способу Верещагина: ;и т.д.

При чистом изгибе кривых брусьев большой кривизны: ;–

радиус нейтр. слоя Для прямоугольного сеч. высотой h, с наружным радиусом R₂ и внутренним R₁: . Приh/R<1/2 . При наличииN: .

Условие прочности: ,y= – h₂ или y= h₁.

Продольный изгиб. Устойчивость. Формула Эйлера: – для стержня с шарнирно закрепленными концами. При различных закреплениях:,

 – коэффициент приведения длины. При шарнирном закреплении обоих концов стержня  = 1; для стержня с заделанными концами  = 0,5; для стержня с одним заделанным и другим свободным концом  = 2; для стержня с одним заделанным и другим шарнирно закрепленным концом  = 0,7.

Критическое сжимающее напряжение.: ,– гибкость стержня, – наименьший главный радиус инерции. Формула Эйлера применима при гибкости стержня: . Для₀<  < _кр используется формула Ясинского: _кр= a — b, где ₀, при котором _кр=_т, a,b – опытные данные, для стали Ст3:

40 <  < 100.

Условие устойчивости: ; [_у]=_кр/n_у; [_у]=[]. – площадь брутто поперечного сечения, т.е. без учета его ослаблений.

Алфавитный указатель абсолютное удлинение	1
внутренние силовые факторы при изгибе	14
временное сопротивление	2
вторая теория прочности	8, 15
геометрические характеристики плоских сечений	10
гибкость стержня	29
гипотеза о не надавливании продольных волокон	15
гипотеза плоских сечений	15
главные моменты инерции	11
главные напряжения	3
главные напряжения при поперечном изгибе	16
главные оси инерции	11
главные площадки	3
главные радиусы инерции	11
главные удлинения	6
главные центральные оси инерции	11
двутавр	10
депланация	14
деформация при объемном напряженном состоянии	6
диаграмма напряжений для пластичных материалов	2
диаграмма напряжений для хрупких материалов	2
дифференциальное уравнение изогнутой оси балки	17
дифференциальные зависимости между М, Q и q	16
дифференциальные зависимости при изгибе	18
допускаемое напряжение	2
единичная сила	25
единичный момент	25
жесткость при изгибе	15
жесткость сечения при кручении	13
жесткость стержня	1
закон Гука	1
закон Гука при изгибе	15
закон Гука при объемном напряжении	6
закон Гука при сдвиге	9
закон парности для объемного напряженного состояния	5
закон парности касательных напряжений	4
закон плоских сечений	13
изгиб	15
изгиб с кручением	22
инварианты напряженного состояния	7
интеграл Мора	25
интенсивность напряжений	5
канонические уравнения метода сил	27
компоненты деформированного состояния	7
координаты центра тяжести	10
косой изгиб	20
коэффициент приведения длины	29
коэффициент продольного изгиба	30
коэффициент Пуассона	1
коэффициент уменьшения допускаемого напряжения	30
кривые брусья (стержни)	27
критическая нагрузка (сила)	29
круг Мора для объемного напряженного состояния	5
круг Мора для плоского напряженного состояния	4
круг Мора при чистом сдвиге	9
кручение	14
кручение бруса прямоугольного сечения	14
кручение круглого бруса (вала)	14
линейное напряженное состояние	2
максимальное касательное напряжение	4
метод Мора – определение перемещений	25
метод начальных параметров – определение перемещений	17
метод сил	27
механические характеристики	2
модуль объемной деформации	6
модуль сдвига	9
модуль упругости	1
модуль упругости 1-го рода	1
модуль упругости 2-го рода	9
модуль Юнга	1
момент инерции кольца	11
момент инерции круга	11
момент инерции относительно параллельных осей	11
момент инерции полукруга	11
момент инерции прямоугольника	11
момент инерции треугольника прямоугольного	11
момент инерции треугольника равнобедренного	11
момент инерции четверти круга	11
момент сопротивления	13
моментом инерции при кручении	14
моментом сопротивления при кручении	14
моменты инерции при повороте осей	12
моменты инерции сечения	10
напряжения на наклонной площадке	3
напряжения по октаэдрической площадке	5
нейтральный слой (ось, линия)	15, 20
неплоский изгиб	20
неразрезные балки	18, 19
нормальные напряжения при чистом изгибе	15
обобщенная сила	24
обобщенное перемещение	24
обобщенный закон Гука	6
объемное напряженное состояние	5
октаэдрическая площадка	5
определение перемещений в балках при изгибе	17
осевой момент инерции сечения	10
осевой момент сопротивления	13
основная система	19
относительная деформация	1
относительная объемная деформация	6
относительная поперечная деформация	1
относительный сдвиг	9
относительный угол закручивания	13
первая теория прочности	8, 16
перемножение эпюр	25
плоский изгиб	15
плоское напряженное состояние	3
площадь	10
положение главных осей инерции	12
полярный момент инерции сечения	10
полярный момент сопротивления	13
поперечный изгиб	15
построение эпюр Q	16
построение эпюр М	16
потенциальная энергия деформации	6
потенциальная энергия при кручении	13
потенциальная энергия при сдвиге	9
предел прочности	2
предел текучести	2
приведенная длина	29
продольный изгиб	29
прямой изгиб	15
радиус инерции	12
радиус кривизны нейтрального слоя	15
раскрытие статической неопределимости балки	18
растяжение	1
расчет на прочность при изгибе	16
сдвиг	9
сжатие	1
сложное сопротивление	20
сложный изгиб	20
собственный вес	1
способ Верещагина	25
способ сравнения перемещений	19
способ фиктивной нагрузки – определение перемещений	18
статически неопределимые балки	18
статически неопределимые системы	27
статический момент сечения	10
статический момент элемента площади	10
степень статической неопределимости балки	18
степень статической неопределимости системы	27
тензор деформаций	7
тензор напряжений	7
теорема Бетли	24
теорема Кастильяно	26
теорема Максвелла	24
теорема о взаимности перемещений	24
теорема о взаимности работ	24
теорема о трех моментах	19
теории предельных напряженных состояний	8
теории прочности	8
теория наибольших касательных напряжений	8
теория наибольших нормальных напряжений	8
теория наибольших относительных деформаций	8
теория прочности Мора	8, 16
теория прочности Мора	8, 16
третья теория прочности	8, 16
угол закручивания	14
угол сдвига	9
уголок	11
удельная потенциальная энергия	6
удельная потенциальная энергия при сдвиге	9
удельное перемещение	24
уравнение изогнутой оси балки	17
уравнение прогибов.	17
уравнение совместности перемещений	19
уравнение трех моментов	19
уравнение углов поворота	17
условие жесткости при кручении	13
условие прочности при кручении	13
условие прочности при растяжении	1
устойчивость сжатых стержней	29
учет собственного веса	1
фиктивная балка	18
фиктивная нагрузка	18
формула Журавского	15
формула Мора	25
формула Навье	15
формула Эйлера	29
формула Ясинского	29
центр тяжести	10
центробежный момент инерции сечения	10
четвертая теория прочности	8, 16
чистый изгиб	15
чистый сдвиг	9
швеллер	11
эллипс инерции	12
энергетическая теория прочности	8
ядро сечения	22

Оглавление

Растяжение и сжатие 1

Учет собственного веса стержня 1

Основные механические характеристики материалов 2

Линейное напряженное состояние 2

Напряженное и деформированное состояние 3

Плоское напряженное состояние 3

Закон парности касательных напряжений 4

Круг Мора 4

Объемное напряженное состояние 5

Круг Мора для объемного напряженного состояния 5

Напряжение по октаэдрической площадке 5

Деформации при объемном напряженном состоянии 6

Потенциальная энергия деформации 6

Тензоры напряжений и деформаций 7

Теории прочности 8

Чистый сдвиг 9

Геометрические характеристики плоских сечений 10

Статический момент 10

Координаты центра тяжести 10

Моменты инерции сечения 10

Моменты инерции сечений простой формы 11

Главные моменты инерции 12

Моменты сопротивления 13

Кручение 14

Изгиб 15

Определение перемещений в балках при изгибе 17

Метод начальных параметров 17

Определение перемещений способом фиктивной нагрузки 18

Статически неопределимые балки 18

Сложное сопротивление 20

Косой изгиб 20

Изгиб с растяжением – сжатием (внецентренное сж.-раст.) 21

Изгиб с кручением 22

Общие методы определения перемещений 24

Теорема о взаимности работ и перемещений 24

Интеграл Мора, способ Верещагина 25

Статически неопределимые системы 27

Канонические уравнения метода сил 27

Расчет плоских кривых брусьев (стержней) 28

Устойчивость сжатых стержней. Продольный изгиб 29

Формулы 31

Алфавитный указатель 40