- •Сокращения:
- •МСС – безмашинная информационная
- •Структуризация знаний и унификация подходов в прикладных науках:
- •(положительные обратные связи).
- •Пример: нужно описать зависимости силы тока и
- •Обычный способ решения.
- •Исследование с помощью МСС
- •Расчет числовых
- •Вольтамперные характеристики (ВАХ) лампы накаливания
- •Чтобы понять технику метода, нужны простые задачи, легко решаемые и без него –
- •Изменение уровня сложности при переходе к МСС
- •Использование МСС «только» для
- •Рис. 7.5. Сообщающиеся сосуды с жидкостью и газом под давлением
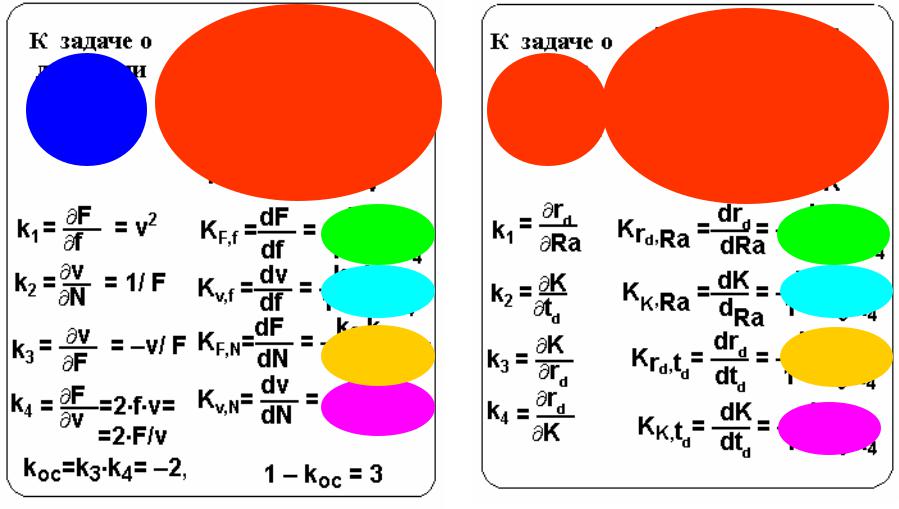
- •Формулы для коэффициентов передачи к схемам предыдущего слайда
- •Сопоставление задач
- •МСС в процедуре дифференцирования
- •Модель экономического равновесия по Кейнсу
- •Разложение производной на аддитивные составляющие
- •Возможности МСС в
- •Математический аспект:
- •Научно-инженерный аспект
- •Педагогический аспект (в прикладных науках)

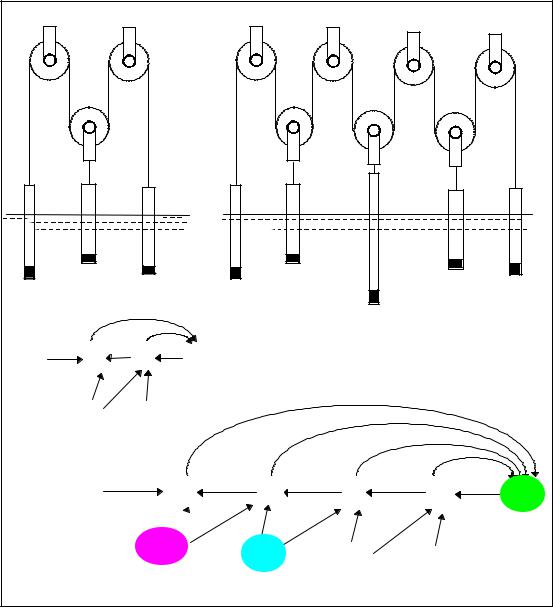
Использование МСС «только» для
наведения на мысль (без вычисления коэффициентов передачи )
о падении с
отрыва).
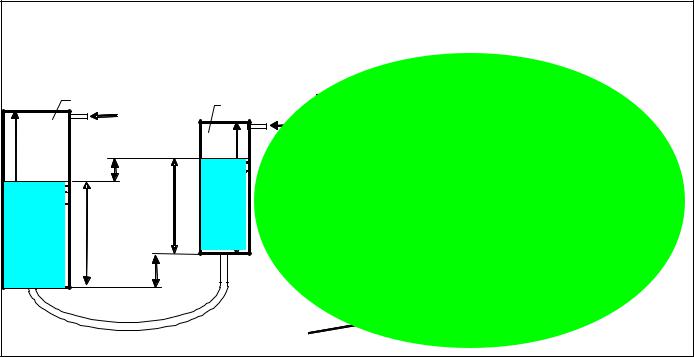
Рис. 7.5. Сообщающиеся сосуды с жидкостью и газом под давлением |
|
P1 |
P2 |
H1 |
|
h |
|
h1 |
h2 |
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Семейство |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
однотипных |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
задач для |
|
|
|
|
|
|
|
|
|
|
|
|
G4 |
|
|
демонстрации |
|
|
|
|
|
|
G |
1 |
|
G |
2 |
|
|
G |
5 |
эффективности |
||
|
k5 |
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
k4 |
|
|
|
|
|
|
G3 |
|
|
|
|
метода при |
|||
G1 |
h1 |
k2 h2 |
k h3 |
|
|
|
|
|
|
|
|
|
|
|
||
|
k1 |
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
переходе от |
|
G2 |
|
G3 |
|
|
k9 |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
k8 |
|
|
k7 |
|
|
k6 |
|
|
простого к |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
G1 |
|
k1 |
k10 |
k2 |
|
k12 |
k3 |
k14 |
k4 |
k16 |
k5 |
|
|
сложному |
|
|
|
|
k11 |
|
k13 |
k15 |
|
|
||||||||
|
|
|
h1 |
|
|
h2 |
|
|
h3 |
|
h4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
G4 |
G5 |
|
|
|
|
|

Формулы для коэффициентов передачи к схемам предыдущего слайда
Koc = k5 (k6 +k4 (k7+k3 (k8 +k2 k9)))
K11 |
|
dh1 |
k1 K51 k5 k4 k3 k2 |
K |
21 |
|
dh2 |
K |
k |
5 |
k |
4 |
k |
3 |
||||
dG1 |
||||||||||||||||||
dG |
||||||||||||||||||
|
|
|
|
|
|
|
|
51 |
|
|
|
|||||||
|
|
|
|
|
dh3 |
|
|
|
1 |
|
|
|
|
|
|
|
||
|
|
|
K31 |
|
K51 k5 k4 |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
dG1 |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
K |
41 |
|
|
dh4 |
K |
51 |
k |
5 |
|
|
|
|
K51 |
|
dh5 |
|
k1 k9 |
|
||||||||||
|
|
|
dG |
|
|
|
|
dG1 |
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 koc |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
K |
12 |
|
dh1 |
k |
10 |
K |
k |
5 |
k |
4 |
k |
3 |
k |
2 |
K52 |
|
|
(k10 k11 k2 ) k9 k11 k8 |
||||||||||||
|
|
|
|
|||||||||||||||||||||||||||
|
|
dG2 |
|
|
|
|
52 |
|
|
|
|
|
|
|
|
|
|
|
|
|
1 koc |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
K53 |
|
|
|
|
|
(k12 k13 k3) (k8 k2 k9 ) k13 k7 |
|
|||||||||||||||||||||
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
koc |
|
|
|
|
|
|
|
|
|
|
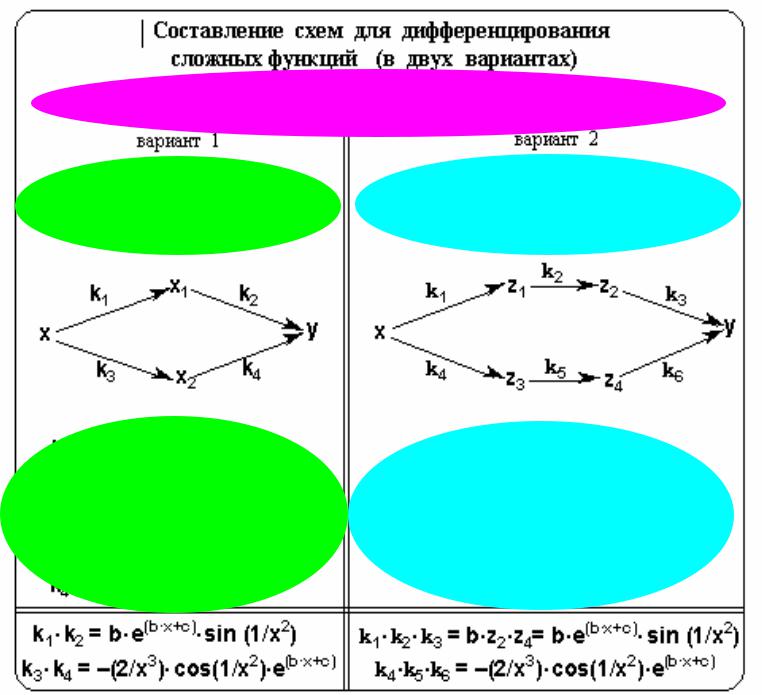
Сопоставление задач
из разных областей знания
|
|
|
|
Сравнение двух способов дифференцирования сложной неявной функции |
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
Функция |
|
y аргумента x задана неявно с помощью системы уравнений : |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
1) y |
|
|
|
z |
2) |
z e |
y w |
|
3) |
v |
z |
2 |
, |
4) w sin v . |
|
Требуется определить ее полную производную: |
|
|
|
|
y' |
|
dy |
? |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
x |
, |
|
, |
|
|
|
|
x |
|
|
|
|
|
|
dx |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
(a) Решение “обычным” способом |
|
|
|
|
|
(b) Решение с помощью МСС |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
(нумерация пунктов – продолжение нумерации исходных уравнений) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
5) |
|
y' z xz 1 xz ln x z' z y |
y ln x z' |
|
|
|
|
(из 1) |
|
|
|
|
|
|
1) Составим |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k6 |
|
|||||||||||||||||||||||||||||||||||||||||
|
z' e y w y' w w' y |
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
6) |
z y' w w' y |
|
(из 2) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
z' |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 z z' |
|
z2 |
|
|
|
|
|
|
|
|
структурную схему |
|
|
|
|
|
|
|
k1 |
|
|
|
|
|
|
k2 |
|
|
|
|
z |
|
|||||||||||||||||||||||||||
7) |
|
y' z |
|
w' y |
(из |
6) |
|
|
|
|
|
8) |
|
v' |
|
|
x |
|
|
|
|
|
x2 |
|
(из 3) |
|
|
|
|
|
|
|
и |
гл |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
y |
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
w |
|
|
|
|
|
|
|
|
2 z z' |
|
|
z |
2 |
|
|
|
|
|
|
|
|
|
|
ум |
|
|
авн |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
9) |
|
w' cos v |
v' cos v |
|
|
|
|
|
|
|
|
|
|
(из 4, 8) |
|
|
|
|
|
|
ст |
|
|
|
|
|
|
ая |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
у |
|
|
в |
|
|
|
|
|
|
|
ч |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
е |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 x |
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
же |
|
|
|
|
нно |
|
|
а |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
в |
|
|
|
|
|
|
|
ст |
|
|
|
|
|
|
k7 |
|
|
|
|
|
|
|
|
k |
|
|
|
|||||||||||||||||||
|
|
|
|
z' |
|
y |
|
|
2 z z' |
|
|
z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ы |
п |
|
|
|
|
й |
|
р |
|
|
ь |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
x |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
о |
|
|
|
|
|
а |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
10) |
|
|
z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
лн |
|
|
|
|
|
бо |
|
|
|
|
|
|
|
|
v |
|
|
|
|
|
|
|
|
|
|||||||||||
y' |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(из 7, 9) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
е |
|
|
|
|
|
|
т |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
w |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
на |
|
|
|
ы |
|
|
|
|
|
|
|
|
|
|
|
|
|
w |
|
||||||||||||||||||||
|
|
z' |
|
|
|
|
|
|
|
|
|
|
|
z2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
! |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k4 |
|
|
|||||||||||
|
|
|
|
|
|
|
2 z z' |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
11) |
|
|
|
y cos v |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2) определим коэффициенты передачи частных связей: |
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
x |
|
|
|
|
|
z y |
|
|
|
|
|
(из |
5, 10) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y ln x z' |
|
|
1) |
k1 z x |
z 1 |
|
|
|
z y |
|
|
|
|
|
|
4) |
|
|
k4 cosv |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
w |
|
|
|
|
|
z2 |
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
z y y cos v |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
о |
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
x |
|
|
|
|
x |
2 |
w |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
г |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z |
|
|||||
|
12) |
z' 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
л |
|
|
|
|
2) |
k2 w e |
y w |
w z |
|
|
|
5) |
k |
|
y z |
|
|
|
7) |
|
k7 |
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
2 z |
|
|
|
(из |
|
|
11) |
|
|
о |
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
z w |
|
y ln x |
y cos v x w |
|
|
|
|
|
|
|
|
|
|
|
|
|
Д |
|
|
о |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
2 |
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
z y |
|
|
|
|
|
|
|
|
|
|
|
|
|
z |
2 |
|
|
|
и |
|
н |
|
|
|
|
|
|
2 z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
y cosv |
|
|
|
|
|
|
|
|
д |
|
|
|
3) |
k3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6) |
k |
|
|
y ln x |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
13) |
|
|
z y |
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
у |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
y' |
y ln x 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x2 w |
|
|
|
н |
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
x |
|
|
|
|
|
|
ln x |
|
|
y cosv |
2 z |
|
|
|
|
|
|
|
|
|
|
|
|
3) Выразим РКП через КПЧС |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
z w y |
|
|
x w |
|
|
|
|
|
|
|
d y |
|
|
|
|
|
|
|
|
k1 1 k3 |
k4 k5 k7 k4 |
k5 k6 |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
z2 y w |
|
|
|
|
|
|
|
|
|
|
|
|
|
z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
z y |
|
|
|
|
|
|
|
|
|
1 cosv |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ky |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
y ln x |
x |
|
|
|
|
|
|
|
|
|
|
|
x w |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
d x |
|
|
|
|
|
|
|
|
1 k2 k6 |
k3 k4 |
k5 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
x |
|
|
|
|
|
1 z w y ln x cosv 2 z2 |
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
z y |
|
|
|
|
|
|
|
|
|
|
|
|
|
2 z2 |
y |
x |
|
|
|
|
|
|
|
z |
2 y w |
|
1 |
cosv |
|
z |
|
и подставим значения этих коэффициентов: |
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
1 z w y ln x cos v |
|
|
|
|
|
|
|
|
|
y |
ln x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
x w |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
3 |
y |
2 |
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
1 z w y ln x cos v 2 z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
z |
|
|
|
|
|
2 z |
2 |
|
|
|
|
z |
|
|
cos v ln x |
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
cos v |
|
|
|
|
2 |
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
d y |
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
z y |
|
|
2 z2 y |
|
|
|
y2 z3 ln x cosv |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
d x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
1 |
cosv |
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
x |
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
w z y ln x |
2 z |
cos v |
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
1 z w y ln x cosv 2 z |
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
(из |
5, 12) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
МСС в процедуре дифференцирования
1.Традиционная организация ДСНФ нарушает основной принцип НОТ: отделять во времени и (или) пространстве разнородные и объединять однородные операции. Здесь разнородны:
(1)собственно дифференцирование,
(2)сопутствующие алгебраические преобразования.
Именно их выполнение вперемешку делает процедуру утомительной и чреватой ошибками.
2. МСС, в согласии с НОТ, разводит указанные компоненты, резко упрощая обе. После составления схемы главная часть умственной работы по ДСНФ уже выполнена. Ее изображение заменяет написание уравнений,
а простые правила свертывания реализуют решение.
Процедура сводится к элементарным действиям без громоздких, трудно проверяемых преобразований.
В постановочной части прикладных задач важны другие свойства метода: дисциплини- рование мышления, структуризация знания.

Модель экономического равновесия по Кейнсу |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
Z - количество денег в обращении |
|
|
|
|
|
|
|
|
|
|
|
|
V – в т.ч. операционный спрос |
|
|
|
|
|
|
|
|
|
|
|
|
Y – в т.ч. Спекулятивный спрос |
|
|
|
|
|
|
w |
|
6 |
|
|
|
Q – объем производства |
|
|
|
|
|
7 |
8 |
|
|
|
S – накопление |
|||
|
|
|
|
|
|
|
|
|
W - потребление |
|||
Z |
1 |
V |
2 |
Q |
3 |
S |
4 |
r |
5 |
Y |
r - банковский процент |
|
- рабочее время |
||||||||||||
|
|
|
|
|
13 |
|
|
|
|
|
||
|
|
|
|
|
|
|
17 |
a |
|
RF – занятость в смене |
||
|
|
9 |
|
|
|
RF |
|
|
RN – общая занятость |
|||
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
a – максимальный уровень |
||
|
|
|
11 |
|
|
|
|
|
|
|
||
|
|
|
|
14 |
|
18 |
|
|
производства при данной занятости |
|||
|
|
12 |
|
|
- обратная величина рабочего дня |
|||||||
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
19 |
|
с поправками |
||
|
|
|
|
|
|
RN |
|
20 |
|
|||
|
|
|
|
|
|
|
|
– технический уровень |
||||
|
|
|
|
|
15 |
|
|
|
||||
s |
10 |
P |
16 |
|
|
|
|
|
производства |
|||
Q' |
|
|
|
b |
21 |
|
b – он же, отнесенный к |
|||||
|
|
|
|
|
22 |
|
|
Q’ – производная производства по |
||||
|
23 |
24 |
|
|
|
|
|
|||||
|
|
|
|
|
|
занятости |
||||||
|
|
|
|
|
|
|
|
|||||
|
|
L |
25 |
|
|
|
|
|
|
|
P – уровень цен |
|
|
|
Lotn |
|
|
|
|
|
s – номинальная зарплата |
||||
|
|
|
|
|
|
|
|
|
L – реальная зарплата |
|||
|
|
|
|
|
|
|
|
|
|
|
Lotn – ее относительное значение |
|