
- •Пример 2. Присоединенный момент
- •Пример 3.
- •Кориолисовы сила и ускорение – продолжение
- •Пример 4.
- •Известен дискомфорт у начинающих от поня- тия мнимого (и комплексного) числа. Он проходит
- •Вектор определяется двумя компонентами – горизонтальной и вертикальной. Чтобы их различать, по горизонтали
- •Для введения операции умножения, он вначале сформулировал правило умножения обычных чисел в таком
- •Геометрическая интерпретация комплексных чисел известна давно. Но именно интерпретация – после того, как

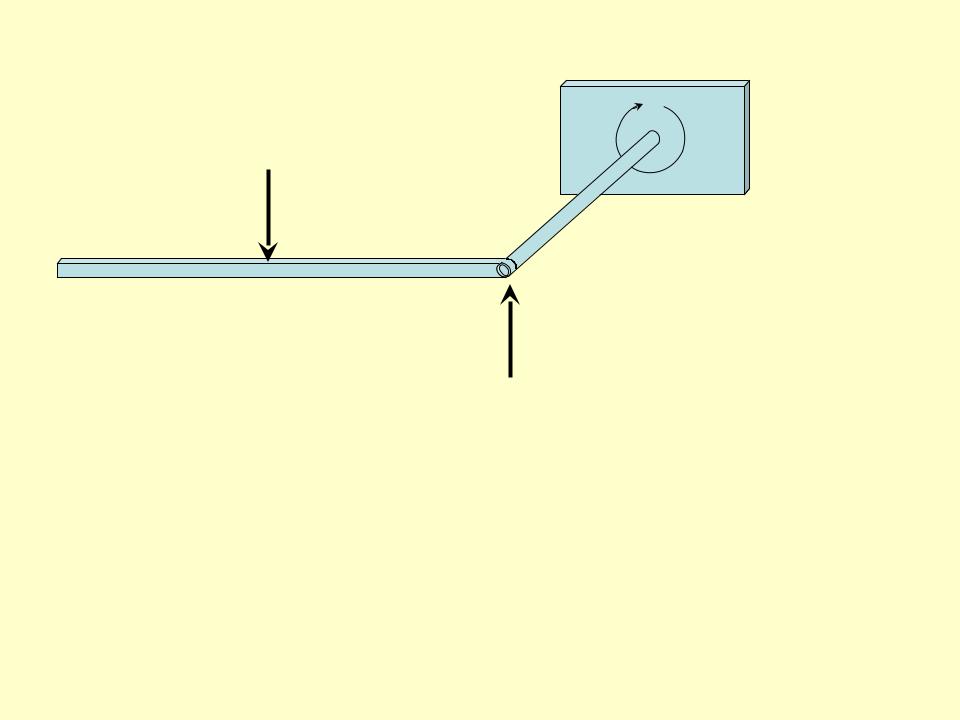
Пример 2. Присоединенный момент
Слышан от проф. С.М. Тарга
Если взять палку рукой за конец и удерживать горизонтально, то сразу почувствуется сила, которая выворачивает руку.
Если держать за середину, то никакого момента не будет: почувствуется только вес.
Так сразу, без всяких формул, можно прочувствовать содержание теоремы о присоединенном моменте.

Пример 3. |
Кориолисовы сила и ускорение возникают |
|
при окружном переносном движении |
Их существование доказывается абстрактными теоретическими построениями, но наглядное представление о их физической природе можно получить, рассматривая предельные случаи
1. Если относительное движение радиальное равномерное:
Абсолютная скорость при движении от центра к периферии возрастает из-за увеличения радиуса вращения. Это и есть кориолисово ускорение и с ним связана сила от стенок жолоба, по которому движется тело. Именно эта сила подмывает берега рек, неравномерно изнашивает рельсы и формирует ураганы.

Кориолисовы сила и ускорение – продолжение
2. Если относительное движение окружное при равных линейных скоростях окружного и переносного движений:
Центробежная сила от переносного движения
Кориолисова
сила
здесь тело в абсолютной системе координат неподвижно, между тем центробежные силы от обоих движений направлены в одну и ту же сторону. Чтобы результирующая сила была нулевой, должно быть еще одно слагаемое, направленное противоположно. Это опять кориолисова сила.
Центробежная сила от относительного движения

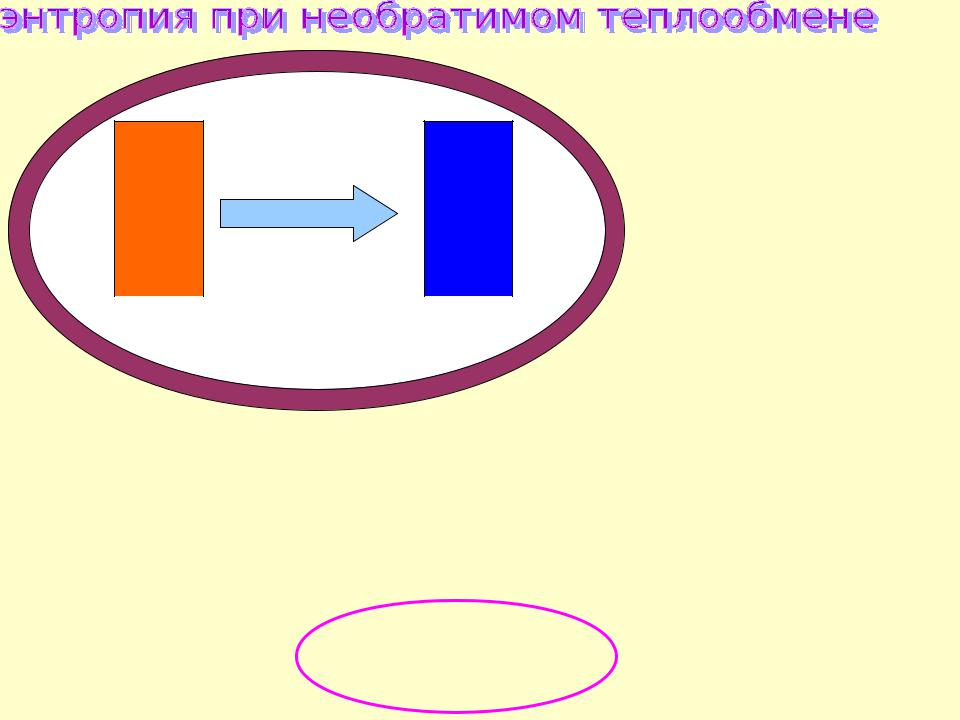
Пример 4. |
Энтропия – характеристическая функция в термодинамике, одно из наиболее абстрактных понятий в науке. Характеризует направление самопроизвольных процессов в изолированной системе.
Считается весьма труднодоступной для понимания, ей даже приписывают мистические свойства.

(См. следующий кадр) >>>
|
q |
dS dq |
|
1 |
|
T |
|
2 |
dq1 |
dq |
|
|
dS |
||
|
1 |
T1 |
T1 |
|
|
||
|
|
T1 |
> T2 |
|
|
|
|
dS2 |
|
dq2 |
|
dq |
|||||
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
T2 |
|||||||||||
|
|
|
|
|
|
dq |
|
dq |
|
|
|
T2 |
|||||
|
|
|
|
|
|
|
|
1 |
|
1 |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
dS dS dS |
|
|
|
|
|
|
dq |
|
|
|
|
|
|||||
|
T |
T |
|
|
T |
||||||||||||
1 |
|
2 |
|
|
|
T |
|
||||||||||
|
|
|
|
|
|
2 |
|
1 |
|
2 |
|
1 |
|
||||
dS 0


1998, |
|
|
|
|
|
|
|
приведено с незначительной редакционной правкой. |
|
|
|
||||
Рассмотрим решение линейного однородного диф уравнения с |
|||||||
постоянны-ми коэффициентами. В случае неравных корней |
|
||||||
характеристического уравнения все просто: имеем два независимых |
|||||||
решения |
1 |
2 |
y ek1 x |
и |
y ek2 x |
k x |
, |
Для случая |
|
|
u x e |
|
|||
k =k |
|
рекомендуют искать решение в виде |
|
|
|||
где u x |
– неизвестная функция, подлежащая определению. |
||||||
Можно сделать иначе. Пусть корни характеристического уравнения отличаются друг от друга на малую величину k.
Линейная комбинация |
e k k x ek x |
|
||
будет естественным решением, так же, как и результат ее деления на |
||||
k. Переходя к пределу, получим |
|
|
|
|
e k k x ek x |
|
dek x |
x ek x |
|
lim k 0 |
k |
dk |
||
Полученное выражение является решением – проверку можно дать в качестве упражнения.
Этот способ лучше традиционного в нескольких отношениях:
1) Исключается немотивированное действие: не навязываем заранее вида решения, а находим его.
2) Работают доказанные ранее теоремы и доказывается их необходимость.
3) Обучаем студента научному поиску.


Известен дискомфорт у начинающих от поня- тия мнимого (и комплексного) числа. Он проходит не от понимания, а от привыкания.
Проф. Ю.В. Линник вводил его способом, свободным от всякого дискомфорта.
Будучи студентом, я слышал его лекции по ТФКП для аспирантов ЛПИ в 1948 г.
Комплексное число - это плоский, то есть двухкоординатный вектор, а сама ТФКП - средство упростить решение плоской задачи: обтекание воздухом крыла самолета, фильтрация воды через грунт под плотиной, электрическое и магнитное поля вокруг линии электропередачи.
