8. Завдання для самостійної підготовки студентів.

8.1 Завдання для самостійного вивчення матеріалу з теми.

8.1.1. Практичне застосування диференціальних рівнянь для розв’язання медико-біологічних задач.

Задача 1.

Збільшення маси m клітини при її зрості описується рівнянням Шмальгаузена та Бордзиловської

де  - стала, пропорційна площі поверхні клітини, характеризує процеси синтезу, а  - стала, пропорційна об'єму, характеризує процеси, протидіючі синтезу.

Визначите часову залежність маси клітини.

Розв’язання.

Поділяючи змінні у рівнянні Шмальгаузена та Бордзиловської, одержимо

.

Інтегруюємо обидві частини рівняння

Інтеграл справа

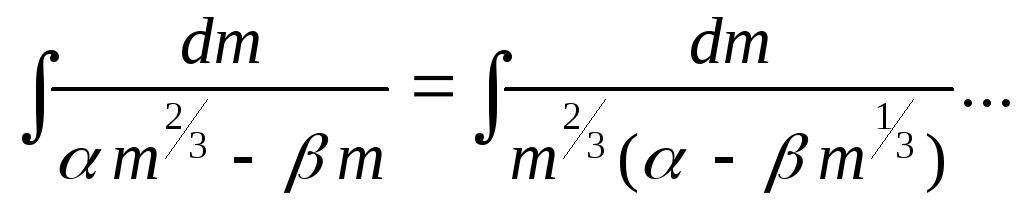
обчислюємо методом заміни змінної

Друга заміна змінної

дає

.

Загальний розв’язок має вигляд

.

Тому, потенціюючи, одержимо

,

тобто

.

Визначимо сталу інтегрування С, відповідну умові

при

,

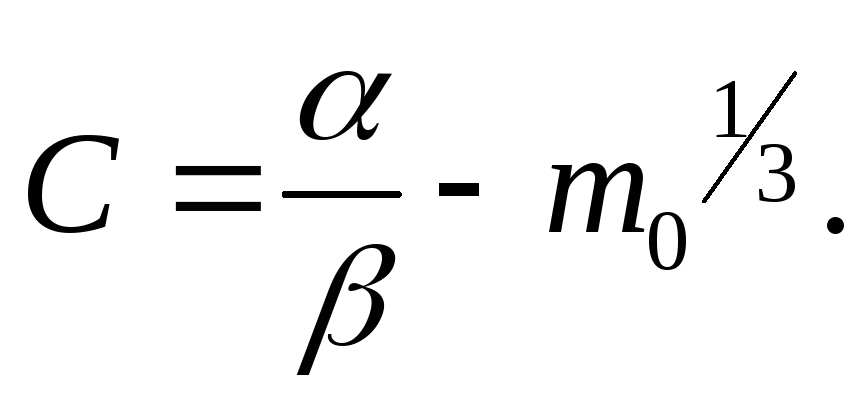
Знайдемо частинний розв’язок, підставляючи знайдене значення сталої інтегрування у загальний розв’язок,

.

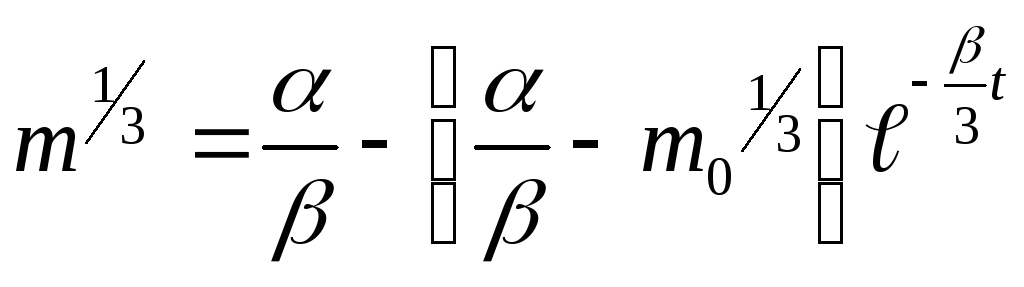отже, залежність маси клітини від часу визначається за формулою

.

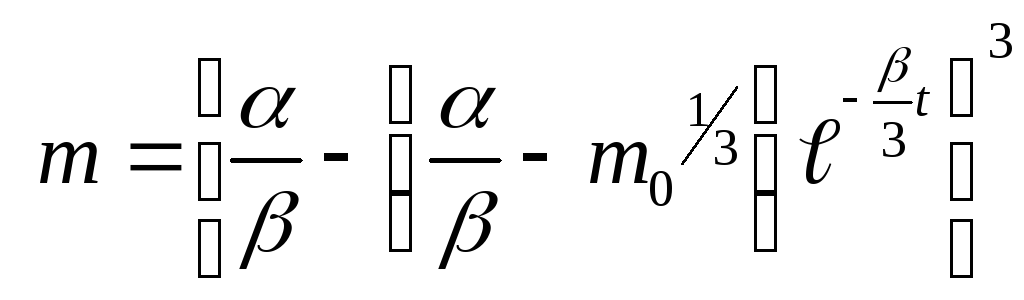Цей частинний розв’язок є шуканою відповідю.

При великих значеннях показника експоненти

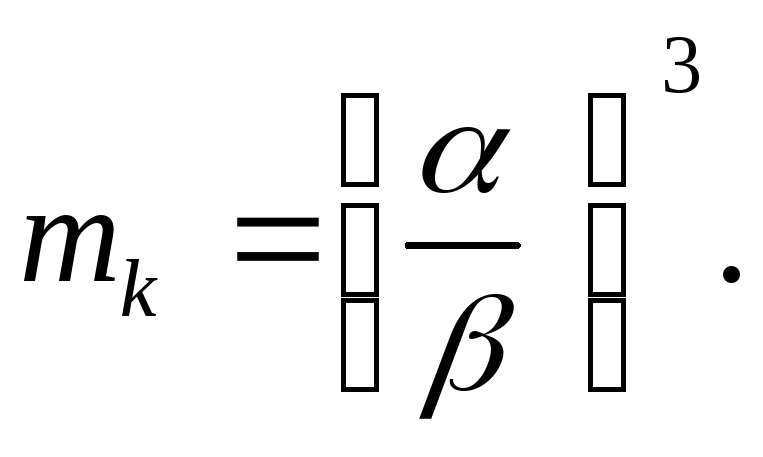
Це означає, що через деякий час настає рівновага між процесами синтезу та розпаду, при цьому досягається кінцева маса клітини.

Задача 2.

Стік крові до периферії під час діастоли описується у межах моделі кровеносної системи, запропонованої О.Франком, диференціальним рівнянням

.

де k - еластичність стінок судин, p - тиск крові, X - гідравлічний опір периферичної частини кровеносної системи, t - час.

Визначити залежність тиску від часу після систоли.

Розв’язання.

Розділимо змінні у диференціальному рівнянні

.

Інтегруючи, одержимо

,

, .

Момент часу t = 0 відповідає кінцю систоли, тому відповідний тиск є систоличним у момент завершення систоли - . З урахуванням цієї обставини шуканий розв’язок має вигляд

.

Ця функція добре описує залежність тиску від часу наприкінці діастоли.

Задача 3.

Швидкість зросту популяції бактерій у момент часу t ( у годинах ) дорівнює розміру популяції x, поділеному на 5.

Опишіть цей процес диференціальним рівнянням та знайдіть за-лежність розміру популяції бактерій від часу.

Розв’язання.

Згідно з умовою, запишемо

Розділимо змінні у диференціальному рівнянні

.

Інтегруємо обидві частини рівняння

,

.

Потенціюємо

.

Вихідний розмір популяції відповідає моменту часу t = 0. Тому початкова умова має вигляд

.

Визначимо сталу інтегрування С, відповідну цій умові:

.

Знайдемо окремий розв’язок, підставляючи знайдене значення сталої інтегрування у загальний розв’язок,

.

Цей окремий розв’язок є шуканою відповідю.

Задача 4.

В експерименті з голодуванням маса m випробуваного за 10 днів зменшилась з 66 до 60 кг. Щоденні втрати маси, згідно спостереженням, були пропорційні масі випробуваного.

Визначити масу випробуваного через 5 днів у цьому експерименті.

Розв’язання.

Складемо диференціальне рівняння. Згідно умові задачи втрата у масі dm пропорційна масі m тіла випробуваного, зрозуміло також, що втрата у масі dm пропорційна інтервалу часу dt, протягом якого вона сталась. Вводячи коефіцієнт пропорційності a, запишемо, виходячи з всього сказаного, таке рівняння

- dm = amdt.

Розділимо змінні у диференціальному рівнянні

.

Інтегруємо обидві частини рівняння

,

.

Потенціюючи, одержимо

.

Момент часу t = 0 відповідає початку експерименту, коли маса випробуваного згідно умові дорівнює 66 кг. Тому початкова умова має вигляд m(0) = 66.

Визначимо сталу інтегрування С, відповідну цій умові:

.

Знайдемо частинний розв’язок, підставляючи знайдене значення сталої інтегрування у загальний розв’язок,

.

Значення коефіцієнта a ми одержимо, використовуючи інформацію про те, що 10 днів пізніше після початку експерименту маса випро­буваного склала 60 кг, тобто, що

m(10) = 60.

Підставимо t = 10 та m = 60 у загальний розв’язок

.

Із цього рівняння легко визначити шуканий коефіцієнт

10a = ln1,1 a = 0,1ln1,1 .

Підставляючи значення коефіцієнта a в частинний розв’язок, одержимо шукану залежність маси випробуваного від часу

.

За допомогою цієї формули можна визначити, чому дорівнює маса випробуваного у будь-який момент часу протягом всього експерименту. Наприклад, через 5 днів маса дорівнює

.

Задача 5.

В регіон занесено інфекційне захворювання. Частка людей p, що перенесли захворювання за t років, описується диференціальним рівнянням

.

За скільки років число перехворівших досягне 90%?

Розв’язання.

Розділимо змінні у диференціальному рівнянні

.

Інтегруємо обидві частини рівняння

.

Інтеграл, що стоїть у лівій частині рівності, обчислимо за допомогою підстановки

z = 1 - p dz = - dp

Одержимо

.

Загальний розв’язок має вигляд

.

Потенціюючи, одержимо

,

При t = 0 захворівших не було, тому початкова умова має вигляд

p(0) = 0.

Визначимо сталу інтегрування С, відповідну цій умові,

0 = 1 - C, C = 1.

Знайдемо частинний розв’язок, підставляючи знайдене значення сталої інтегрування у загальний розв’язок,

.

Щоб визначити, за скільки років частка перехворівших досягне 90 відсотків, підставимо у цю формулу p = 0,9 та обчислимо якому значенню t відповідає це значення p.

, ,,.

Отже, за 4,6 року перехворіє 90% населення.

Задача 6.

В моделі епідемій один заражений індивідуум вводиться у спільноту, що складається з n індивідуумів, сприйнятливих до даного захворювання. Нехай чисельність незаражених індивідуумів дорівнює x(t). Відомо, що зменшення x(t) описується диференціальним рівнянням

dx = - rx(n + 1 - x)dt,

де r - частота контактів між членами спільноти, від якої залежить швидкість розповсюдження інфекції.

Знайдіть розв’язок цього диференціального рівняння.

Розв’язання.

Розділимо змінні у диференціальному рівнянні

.

Інтегруємо обидві частини рівняння

.

Інтеграл у лівій частині рівності можна вирахувати, взявши до

уваги, що

Підставляючи цей розклад у інтеграл, одержимо

.

Другий інтеграл обчислюється підстановкою

z = n + 1 - x, dz = - dx.

Об’єднуючи ці результати, маємо

.

Загальний розв’язок має вигляд

.

Потенціюючи, одержимо

, .

Перед початком епідемії число сприйнятливих дорівнює числу людей у спільноті, тобто

x(0) = n.

З урахуванням цієї початкової умови визначимо сталу інтегрування

, .

Знайдемо частинний розв’язок, підставляючи знайдене значення сталої інтегрування у загальний розв’язок,

.

На практиці під час епідемії реєструється звичайно число нових випадків захворювання, що з'являються за добу або за тиждень. Тому зручніше розглядати динаміку зростання числа нових випадків, що описується формулою

.

Графік цієї функії називається епідемічною кривою. Ця крива спочатку росте, досягає максимуму при

і далі зменшується до нуля. Таким чином, епідемічна крива описує характерну властивість епідемій: число нових випадків спочатку швидко зростає, у якийсь момент часу досягає максимуму, а потім зменшується до нуля.

8.1.2. Задачі для самостійного розв’язання

1. Якщо харчовий ресурс зберігається не дивлячись на зріст чисельності популяції, то, як показав Мальтус, цей зріст описується диференціальним рівнянням

,

де x - чисельність популяції у момент часу t , k - стала.

Одержати загальний розв’язок рівняння Мальтуса.

2. Розв’язати рівняння Ферхюльста, що описує зріст чисельності дуже великих популяцій,

,

де k та l -сталі.

3. Вицвітання зорового пурпуру під дією світла належить до числа простих фотохімічних реакцій. Протягом перших 0,01 - 0,1 с кінетика такої реакції описується рівнянням

.

де R - концентрація родопсину, t - час, відрахований від моменту включення світла, k - константа швидкості реакції,  - частка падаючого світла, захопленого родопсином, I - інтенсивність падаючого світла.

Одержати загальний розв’язок.

4. Залежність швидкості v течії крові у артерії від відстані r від осі артерії описується рівнянням

,

де та- тиски на кінцях ділянки артерії, - в'язкість крові, l - довжина ділянки артерії.

Одержати загальний розв’язок.

5. Залежність заряду q , що проходить через біологічну тканину з опором R та ємністю C , при розмиканні кола описується рівнянням

.

Одержати загальний розв’язок.

6. Ослаблення внаслідок поглинання інтенсивності світла dI, що проходить через шар розчину біологічної рідини товщиною dx, описується законом Бугера

dI = - kIdx,

де k - натуральний показник.

Знайти інтегральну форму закону Бугера.

7. Зменшення концентрації dn молекул, вступаючих у фотохімічну реакцію під дією світла, описується формулою

,

де - інтенсивність падаючого світла,- площа ефективного перетину молекул для фотохімічного перетворення.

Знайти залежність концентрації молекул, вступаючих у фотохімічну реакцію, від часу.

8.1.3. Контрольні запитання

1. Які рівняння називаються диференціальними?

2. Звичайні диференціальні рівняння.

3. Порядок диференціального рівняння.

4. Загальний розв’язок диференціального рівняння.

5. Окремий розв’язок диференціального рівняння.

6. Диференціальні рівняння з розділяючимися змінними.

7. Диференціальні рівняння у частинних похідних.