Корольов / Задач_ТЕКС
.docxПРИКЛАДИ ВИРІШЕННЯ ТИПОВИХ ЗАДАЧ
(до екзамену з дисципліни ТЕКС).
І. Аналіз електричних кіл постійного струму, методи еквівалентних перетворень
Дві схеми еквівалентні, коли струм і напруга в не перетвореній частині схеми залишаються незмінними.
Задача1. Для електричного кола зображеного на рис. 1.1 визначити еквівалентні опори між зажимами 11 -1, 2- 21, якщо R1=6Oм, R2=15 Oм, R3=5Oм, R4=30Oм,
R5=6Oм.
2
R3
1
R1
2



R5
R4
R2











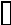
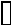
R2-21
=
11
21
21









Розв’язання:
1.Визначити еквівалентний опір між затискачами 1-11
Резистори R4 іR5 з’єднанні паралельно , тому еквівалентний їм опір
R4,5=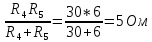
Знайдений опір R4,5з’єднано послідовно з опором R3, виходячи з цього ,
R3, 4, 5 = R3+ R4,5= 5+5 =10Ом
Внаслідок еквівалентий опір елестричного кола між зажимами 1-11 складається з опору R4до якого послідовно підключенні два паралельно підключених між собою опори R2 і R3,4,5
R1-1=
R1
+
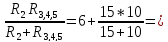 1Oм
1Oм
2. Визначаємо еквівалентний опір між зажимами 2- 21.
Відносно зажимів 2-21 опір R4, R5 і (R2+R3) з’єднанні паралельно, як наслідок,
 +
+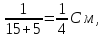
звідси R2-2=4 Ом.
Опір R2-2 можна визначити по-іншому:
R2
-2=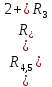
Задача №2

Відомі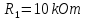 ;
;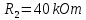 ;
;
 .
.
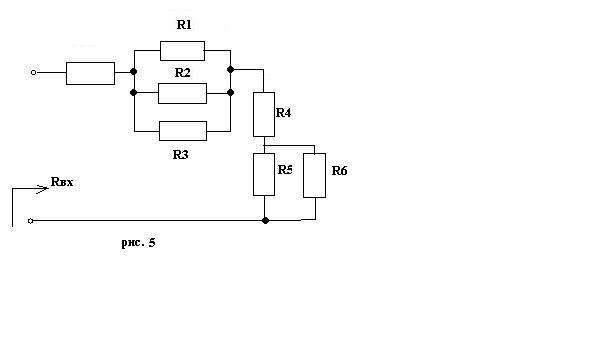
Знайти вхідний опір і вхіднупровідність.
Розв’язок:
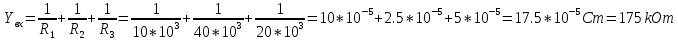

Задача №3
Відомі
: 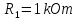

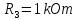


Знайти:
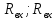
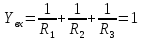



Аналіз електричних кіл при послідовному з’єднанні
Задача №4
Відомі ;
;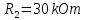 ;
;
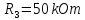 .
.
Знайтивхіднийопір і вхіднупровідність.
Вирішення:
Аналіз електричних кіл при паралельному і змішаному з’єднанніелементів
Задача №5
Визначити величини струмів і напруг на елементах схеми рис. 1.1:
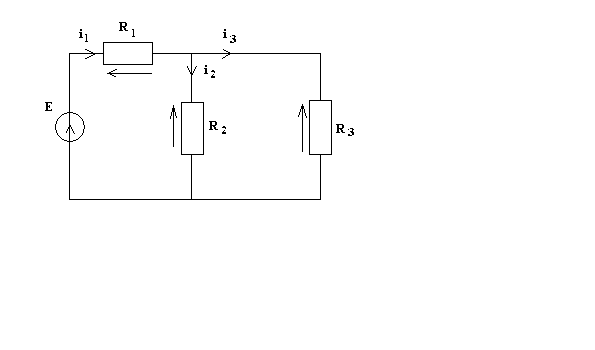 рис.
1.1
рис.
1.1
Дано: E = 20 B
 =20Oм
=20Oм
 =10Oм
=10Oм
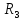 =30Ом
=30Ом
Розв'язання:
-
Розраховуємо вхідний опір

-
Знаходимо загальний стум :
I1=
-
По закону Ома визначаємо напругу на R2:
UR2=I1
4.Розраховуємо струми:
I2=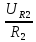 =
=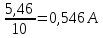
I3=I1-I2=0,726 -0,546=0,18A
2.1Алгебраїчні дії з комплексними числами
Будь-яке комплексне число Ȧ можливо записати у показниковій, тригонометричній або алгебраїчній формах.
 =
Ae±јα=Acosα±јAsinα=a±јb
=
Ae±јα=Acosα±јAsinα=a±јb
Де
A= - модуль комплексного числа;
- модуль комплексного числа;
Α=arctg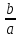 -
аргумент
комплексного числа;
-
аргумент
комплексного числа;
a=Acosα=R2(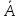 )
- дійсна
частина числа;
)
- дійсна
частина числа;
b=
Asinα=Im( )
- уявна
частина числа;
)
- уявна
частина числа;
Алгебраїчна форма відповідає зображеню числа Ȧ у вигляді точки на комплексній площині в декартових координатах, а показникова у вигляді вектора довжиною Ȧзвернутого на кутα.
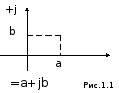
Показникову
форму запису можна отримати з прямокутного
трикутника
 =
Aeјα
=
Aeјα
A=
Α=arctg
Зв’язок між показниковою і тригонометричною формами отримуємо з формули Ейлера
e±јα=cosα±jsinα
При розрахунках з допомогою комплексних чисел зазвичай доводиться переходити від однієї форми запису до іншої. Наприклад, для додаання(віднімання) комплесних чисел застосовують алгебраїчну форму запису. При цьому окремо додають (віднімають) дійсні і уявні частини чисел.
Показникова форма комплекного числа найбільш зручна для множення і ділення чисел.
У цьому випадку модулі чисел перемножують (ділять), а аргументи додають(віднімають).
Приклад.
Дано два комплексних числа:
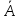 1=5+j3,5;
1=5+j3,5;
 2=1,8-j4.
2=1,8-j4.
Знайти суму, різність, добуток і похідну цих чисел.
Рішення.
При додаванні чисел отримаємо:
 =
=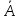 1+
1+ 2=(5+j3,5)+(1,8-j4)=(5+1,8)+j(3,5-4)=6,8-j0,5.
2=(5+j3,5)+(1,8-j4)=(5+1,8)+j(3,5-4)=6,8-j0,5.
Різність цих чисел дорівнює:
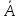 =
=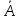 1-
1- 2=5+j3,5-1,8+j4=3,2+j7,5.
2=5+j3,5-1,8+j4=3,2+j7,5.
Для множення і ділення запишемо числа в показниковій формі:
 1=
1=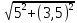 ejarctg(3,5/5)=6,1ej35
ejarctg(3,5/5)=6,1ej35
 2=
2=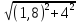 e-jarctg(4/1,8)=4,39e-j65,8
e-jarctg(4/1,8)=4,39e-j65,8
Тоді
 =
= 1
1 2=6,1ej35O4,39e-j65,80=26,78ej(35o-65,8o)=26,78e-j30,8
2=6,1ej35O4,39e-j65,80=26,78ej(35o-65,8o)=26,78e-j30,8
 =
= =
= =1,39ej(35o+65,8o)=1,39ej100
=1,39ej(35o+65,8o)=1,39ej100
2.2. Оригінали та зображення гармонічного струму і напруги
Миттєвий гармонічний струм і напруга називають оригіналами:
i(t)=Imsin(ωt+Ψj) ; u(t)=Umsin(ωt+Ψu);
де Im, Um - амплітуди коливнь;
Ψj, Ψu - початкові фази коливань.
Зображення гармонічних струмів (напруг)
İm(t)=Imej(ωt+Ψi) - комплекс миттєвих значень струму
İm=ImejΨi- комплексна амплітуда струму
İm=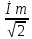 - комплексний струм
- комплексний струм
Зображення похідної та інтегралу від гармонічної
 =jωİm
;
=jωİm
; =
= İm
İm
2.3 Комплексні опір і провідність кола
При розрахунку кола комплексним методом вводиться поняття комплексного опору ( провідності).
Комплексним опором Z називаєтьсявідношеннякомплексноїнапруги до комплексного струму, викликаногоцієюнапругою.
Z
= =
=
 =
=
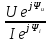 =
=
 -
-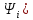
Засттосовують три форми запису:
Z
= =ᴢcosϕ
+jsinϕ
=r +jx
=ᴢcosϕ
+jsinϕ
=r +jx
де
z =
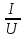 =
=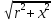 – повнийопір струму;
– повнийопір струму;
R = zcosφ – активний опір;
X = zsin φ – реактивний опір;
φ
=
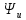 -
-
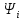 = arctg
= arctg – зсув фаз
– зсув фаз
Комплексною провідністю Y називається відношення комплексного стуму до комплексної напруги:
Y
= =
=
 =
=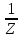 =
=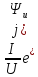 -
-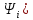
На основі цього запишемо :
Y
= y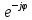 = ycosφ
+jy(-sinφ) = G+jB
= ycosφ
+jy(-sinφ) = G+jB
де
y =
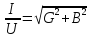 – повнапровідність;
– повнапровідність;
G=ycosφ – активна провідність;
B= ysinφ – реактивна провідність.
Комплесний опір індуктивності
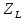 =
j
=
j L
– алгебраїчнаформа
L
– алгебраїчнаформа
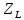 =
=
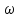 L
L – показникова форма
– показникова форма
±j
=
 =
cos
=
cos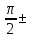 jsin
jsin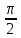 =0 ±j
=0 ±j
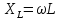 –реактивний
опір
індуктивності (Ом)
–реактивний
опір
індуктивності (Ом)
Комплексний опір ємності :
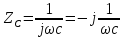 -
алгебраїчна
форма
-
алгебраїчна
форма
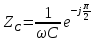 -
показникова форма
-
показникова форма
 -
реактивнийопірємності (Ом)
-
реактивнийопірємності (Ом)
2.4 Вирішення типових задач
Задача№6
Електричне коло утворене послідовним з’єднанням двох пасивних елементів. Визначити напругу на вході кола, її опір і провідність, якщо струм в колі
i(t)
=30cos
(4* t
- 20
t
- 20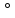 )мA,
а напруга
на елементах
дорівнює:
)мA,
а напруга
на елементах
дорівнює:
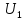 (t)
= 5cos (4*
(t)
= 5cos (4* t
+50
t
+50 B;
B;
 (t)
= 3cos
(4*
(t)
= 3cos
(4*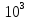 t
-10
t
-10 B.
B.
Построїти векторну діаграму.
U(t)
=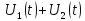
Cкористаємось комплексним методом. Найдемо зображення напруг:


Звідсиотримаємо комплексні амплітуди напруг:
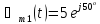 В
В
 В
В
Тоді комплексна амплітуда на вході рівна:
 =
=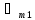 +
+ =
=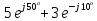
Залишаємо складові в алгебраїчній формі:
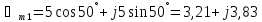
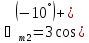 j3sin
(
j3sin
(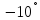 )=
2,95 – j0,521
)=
2,95 – j0,521
Післясумуванняотримаємо:
 B.
B.
Знайдемооригінал (миттєве значення ) напруги.
Для
цього помножимо
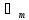 на оператор обертання
на оператор обертання
 і поформуліЕйлеранайдемореальнучастину
(так як вихіднанапруга є функція косинуса)
комплексного числа:
і поформуліЕйлеранайдемореальнучастину
(так як вихіднанапруга є функція косинуса)
комплексного числа:
U(t)
=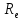 {δ,99
{δ,99 }
= 6,99 cos(4*
}
= 6,99 cos(4* )
B.
)
B.
2. Визначимоопір і провідність кола і їїелементів . Комплексна амплітуда струму дорівнює:
 мА
мА
Тоді за законом Ома отримаємо :
Z
=
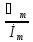 =
=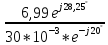 = 233
= 233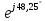 Ом.
Ом.
Звідси:
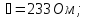
r
= ᴢcos
φ = 233 cos 48,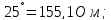
х
= ᴢsinφ
= 233 sin48, =
173,8 Ом
=
173,8 Ом
Знайдемо опір елементів. в послідовному колі в кожному елементі проходить один і то й же струм , тому
 =
=
 =
= = 166,7
= 166,7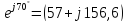 Ом.
Ом.
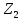 =
=
 =
=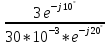 = 100
= 100
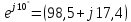 Ом.
Ом.
Знайдемопровідність в колі:
Y
=
 =
= = 0,0043
= 0,0043 См;
См;
Звідси:
y=0,0043 См;
g=ycosφ
=0,0043cos
48,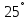 =
0,00286См;
=
0,00286См;
в=ysinφ=
0,0043 sin
48,
Аналогічно знайдемо провідність елементів:
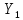 =
=
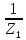 =
=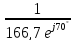 = 6
= 6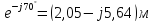 См;
См;
 =
=
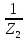 =
=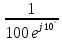 = 10
= 10 См.
См.
Задача №7
На
вхід електричного кола подано напругу
U(t) = 10 sin (4*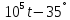 )
B.
Розрахувати струм на вході і потужність
в колі, якщо її комплексний опір дорівнює
)
B.
Розрахувати струм на вході і потужність
в колі, якщо її комплексний опір дорівнює
Z
=
5*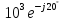 Ом.
Ом.
Розв’язання
-
Розрахуємо струм в колі . Запишемо комплексну амплітуду (зображення) напруги:
 В.
В.
За законом Ома розрахуємо комплексну амплітуду струму в колі:
 =
=
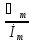 =
= = 2 *
= 2 * A
A
Помножимокомплекснуамплітуду струму наоператоробертання ы за формулою Елеразнайдемооригигінал струму (миттєвезначення):
i(t)=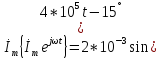 )A.
)A.
-
Розраховуємо потужність в колі. Знайдемо складові комплексного опору:
R=zcosφ=
5*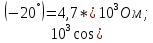
х=zsinφ=
5*
Далівикористовуюча активна потужність кола:
P
= R* =
R
=
R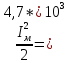 *(2 *
*(2 *
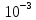 )
)
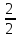 =
9.4 м Вт
=
9.4 м Вт
Реактивнапотужність:
Q=
x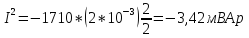
Повна потужність в колі:
S=
 =
= = 10мВА
= 10мВА
Потужнністьможна розрахувати іншим шляхом
S
= UI =
 =
10Мв
=
10Мв
P
= Scos φ = 10 cos (- )
= 9,397мВт;
)
= 9,397мВт;
Q
= Ssin φ = 10 sin (-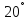 )
= -3,42мВAр.
)
= -3,42мВAр.
Задача №8 Скласти за методом рівняньКірхгофа систему рівнянь для розрахункуструмів в гілках кола (рис. 3.4).
Задамося умовно позитивними напрямками струмів в гілках і напруг на елементах (див. рис. ), а також напрямами обходу контурів.
Вважаючи
вузли 1, 2, 3 і 4 незалежними, складемо для
них рівняння за першим законом Кірхгофа:
для 1-го вузла: - і1 – і2 + і3 = 0;
для 2-го вузла: і2 – і4 + і5 + і6 =0;
для 3-го вузла: - і3 – і5 + і8 – і = 0;
для 4-го вузла: і1 – і4 - і7 = 0.
Струми, спрямовані до вузла, враховуються в рівнянняхзі знаком (+), спрямованівідвузла - зі знаком (-). 4. Вибравшинезалежніконтури І-ІУ (див. рис. 4), складемо для них рівняння за другим законом Кірхгофа:
для
1-го контура: - і1Z1+
і2Z2
+ і4Z4
=
-
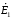 ;
;
для
2-го контура: - і4Z4+
і6Z6
+ і7Z7
=
-
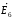 ;
;
для
3-го контура: - і5Z5+
і8Z8
+ і6Z6
=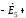
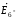
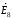 ;
;
для
4-го контура:- і1Z1+
і2Z2
+ і4Z4
=
-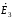 +
+ .
.
Примітка . Падіння напруг на елементах контурів висловимо через - шукані струми в гілках.Спільне рішення отриманих восьми рівнянь дозволяє розрахувати всі невідомі струми в гілках , а потім , якщо необхідно , напруги на елементах ланцюга.З наведеного прикладу видно , що перевага методу рівнянь Кірхгофа полягає в його простоті (з точки зору складання рівнянь). Недолікцього методу - складністьвирішеннясистемирівнянь за великого числа рівнянь та їхрізнорідності .