Задача 3

Первинний двійковий цифровий сигнал передається гауссовим каналом зв’язку з білим шумом модульованими сигналами і може бути прийнятий когерентним і некогерентним способами.

Для заданих модульованих сигналів і способів приймання необхідно:

1. Записати алгоритми роботи оптимальних демодуляторів, навести структурні схеми демодуляторів, які реалізують ці алгоритми. Пояснити особливості алгоритмів і схем.

2. Розрахувати та побудувати залежність імовірності помилки p від відношення 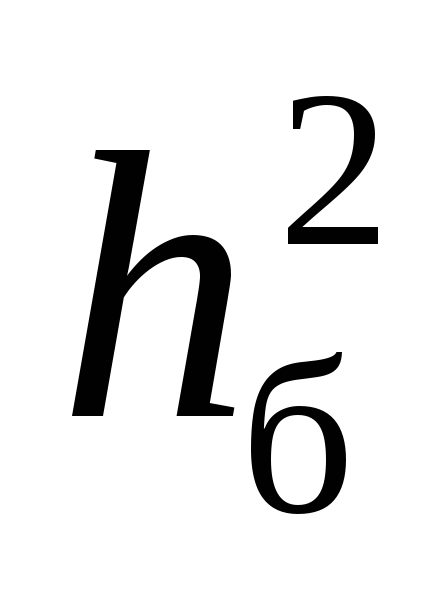 = E_б/N₀, де E_б – середня енергія, що витрачається на передавання біта; N₀ – спектральна густина потужності білого шуму. Межі змінення ймовірності помилки 10^–2 > p > 10^–5.

3. Визначити енергетичні втрати (програш) некогерентного приймання порівняно із когерентним при заданій ймовірності помилки.

Вихідні дані до задачі 3 наведено в таблиці 4.

Таблиця 4 – Вихідні дані до задачі 3

Передостання цифра номера залікової книжки	Вид модульованого сигналу	Імовірність помилки p
0	ВФМ-2	10–3
1	ЧМ-2	5·10–4
2	АМ-2	10–4
3	ВФМ-2	5·10–4
4	ЧМ-2	10–5
5	АМ-2	3·10–5
6	ВФМ-2	3·10–5
7	ЧМ-2	3·10–5
8	АМ-2	4·10–5
9	ВФМ-2	4·10–5

Вказівки. Дивіться[1, с. 256-277; 2, с. 169-192, 197-204; 3, с. 163-197].

Для розрахунків імовірності помилки за п. 2 слід задаватися значеннями h = E_б /N₀, починаючи з h = 8 дБ для АМ-2, ЧМ-2, h = 6 дБ для ВФМ-2 і збільшувати h з кроком 2 дБ доти, поки ймовірність помилки не стане меншою за 10^–5.

У розрахункові формули значення h (чи h_б) слід підставляти в разах: h = 10

Задача 4

Сигнали аналогової модуляції передаються гауссовим каналом зв’язку з білим шумом. Приймання оптимальне.

Необхідно:

1. Пояснити, як оцінюється завадостійкість при демодуляції сигналів аналогової модуляції.

2. Пояснити, що таке оптимальний лінійний фільтр Колмогорова-Вінера (ОЛФ), навести його характеристики (АЧХ і ФЧХ). Навести структурну схему оптимального демодулятора сигналів аналогової модуляції на базі ОЛФ.

3. Розрахувати та порівняти між собою необхідні потужності сигналів на входах демодуляторів ЧМ і АМ при прийманні розмовного сигналу зі смугою частот 300…3400 Гц.

4. Пояснити, що таке оптимальний індекс частотної модуляції. Визначити оптимальний індекс сигналу ЧМ при заданих коефіцієнті амплітуди первинного сигналу К_А та відношенні сигнал/шум на виході демодулятора ρ_вих. Вихідні дані наведено в таблиці 5.

5. Пояснити, що таке поріг завадостійкості при ЧМ. Навести структурні схеми пристроїв для зниження порогового відношення сигнал/шум, пояснити принцип їх роботи.

Таблиця 5 – Вихідні дані до задачі 4

Передостання цифра номера залікової книжки	N0, В2/Гц	ρвих, дБ	mАМ	mЧМ	КА
0	10–8	50	0,8	3	3
1	10–7	47	0,6	4	3,5
2	10–6	43	0,5	5	4
3	2·10–6	40	0,4	6	4,5
4	2·10–7	37	0,3	7	5
5	2·10–8	45	0,45	8	4,5
6	5·10–8	35	0,55	7	4
7	5·10–7	43	0,65	6	3,5
8	5·10–6	53	0,75	5	3
9	3·10–8	38	0,85	4	5

Вказівки. Дивіться [1, с. 335-339; 2. с. 307-329; 3. с. 207-222, 225-232].

Завадостійкість демодуляторів сигналів аналогових видів модуляції можна оцінити виграшем у відношенні сигнал/завада

g = ρ_вих/ρ_вх,

де ρ_вх і ρ_вих – відношення сигнал/завада на вході та виході демодулятора, відповідно.

Для ЧМ ρ_вх = P_s/P_n = P_s/(N₀F_ЧМ) вибирають так, щоб забезпечити роботу демодулятора вище порога ρ_вх > ρ_пор = 10 (або 10 дБ),

де ρ_пор – порогове відношення сигнал/шум на вході демодулятора сигналу ЧМ.

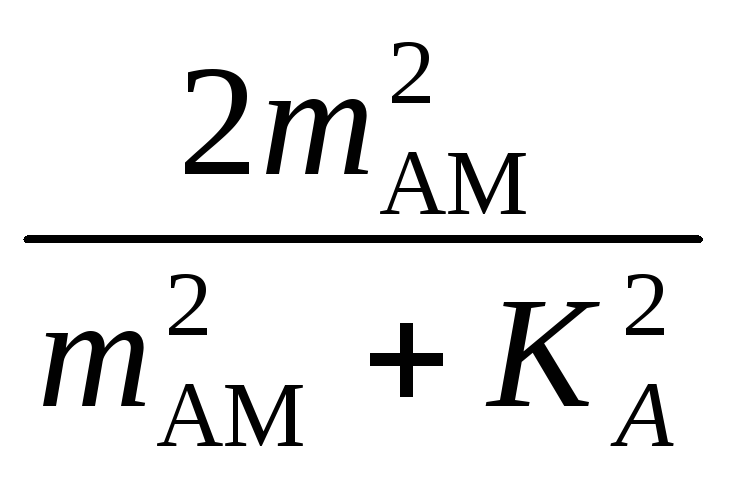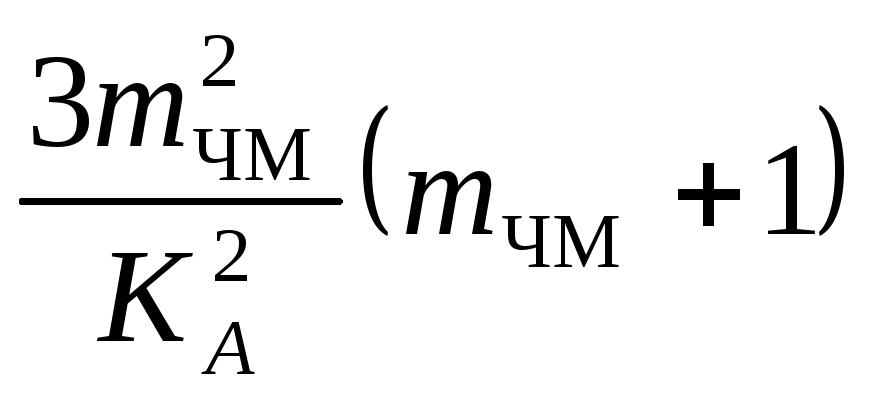g_АМ = ,g_ЧМ = , для>>1 виграш g_ЧМ

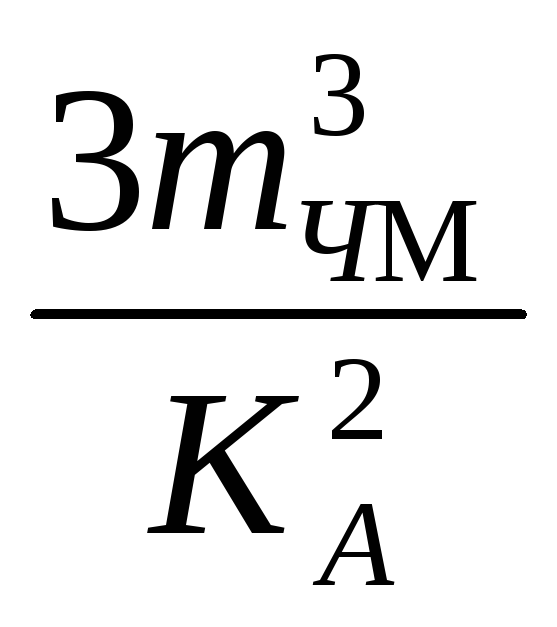
де m – коефіцієнт амплітудної модуляції,

–індекс частотної модуляції.

Для визначення оптимального індексу ЧМ слід прийняти >>1 і ρ_вх = ρ_пор = 10.

Схеми демодуляторів зі зниженим пороговим відношенням сигнал/шум можна знайти в [1, c. 446, 447].