Задача 2

Сигнал s(t) задан в задаче 1, там же определеноF_max.

Необходимо:

1. Определить интервал дискретизации Т_д, представить таблицу отсчетовs(kТ_д), построить график дискретного сигналаs_д(t).

2. Определить частоту дискретизации f_ди построить график амплитудного спектра отсчетов для области частот 0f2f_д. Показать на графике граничные частоты полосы пропускания и полосы задерживания фильтра, восстанавливающего сигнал по отсчетам.

3. Привести схемы аналого-цифрового преобразователя (АЦП) и цифроаналогового преобразователя (ЦАП); пояснить принципы аналого-цифрового и цифроаналогового преобразований; представить сигнал s(t) цифровым сигналом, определить длительность двоичного символаТ_б.

Указания к решению задачи 2

Задача 2 связана с двумя темами – это “Теорема Котельникова” и “АЦП и ЦАП”. Соответствующие сведения по этим темам можно найти в литературе [1, разд. 2.7– 2.9].

Расчет интервала дискретизации и отсчетов сигнала

Согласно теореме Котельникова при дискретизации сигнала s(t) интервал дискретизацииТ_дне может превышать значение 1/(2F_max), гдеF_max– максимальная частота спектра сигналаs(t). ЗначениеF_maxнайдено в задаче 1. Целесообразно выбратьТ_д= (0,7...0,8)/(2F_max). Эту целесообразность хорошо будет видно ниже из графика рис. 4 при определении граничных частот полосы пропускания и полосы задерживания восстанавливающего ФНЧ.

Отсчеты сигнала s(t) – это значенияs(kT_д), гдеk=k_min,..., –2, –1, 0, 1, 2,...,k_max;k_minиk_max– номера крайних отсчетов, которые определяются из условия –b/2 ≤k_minT_диb/2 ≥k_maxT_д. Заданные в КР сигналы – четные функции, поэтомуk_min= –k_max.

Пример 5. В примере 4 найдено значения максимальной частоты спектра сигналаs(t):F_max= 27 Гц. ТогдаТ_д= (0,7...0,8)/(2F_max) = (0,7...0,8)/(227) = (13,0...14,8) мс. ПримемТ_д = 14 мс. Рассчитаем отсчеты сигналаs(t), аналитическое выражение которого приведено в примере 1. Рассчитанные отсчеты представлено в табл. 3.

Таблица 3 –Отсчеты сигнала, квантование отсчетов и кодирование уровней квантования

k	kTд, мс	s(kTд), мВ	s(kTд)/s	р(kTд)	sкв(kTд), мВ	кв(kTд), мВ	Кодовые комбинации
–2	– 28	25,5	12,75	13	26	+0,5	01101
–1	– 14	43,9	21,95	22	44	+0,1	10110
0	0	50,0	25,0	25	50	0	11001
1	14	43,9	21,95	22	44	+0,1	10110
2	28	25,5	12,75	13	26	+0,5	01101

График дискретного сигнала s_д(t), построенный на основе рассчитанных отсчетов, приведен на рис. 3.

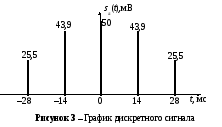
Построение графика спектра дискретного сигнала

Для построения графика достаточно помнить, что спектральная плотность отсчетов является суммой периодических повторений с периодом частоты дискретизации f_дспектральной плотности непрерывного сигналаS(f) умноженной наf_д(частота дискретизацииf_д= 1/Т_д– величина, обратная к интервалу дискретизации):

S_д(f) = , –   f.

При изображении амплитудного спектра дискретного сигнала определяют модуль S_д(f) и показывают график для области значений f  0. Для получения представления о спектре S_д (f) достаточно рассчитать частичную сумму ряда для членов с номерами n = 0, 1 и 2.

Пример6. Спектральную плотность непрерывного сигнала из примера 1 найдено в примере 2, а интервал дискретизации – в примере 5. Частота дискретизацииf_д= 1/Т_д= 1/(1410^–3) = 71,4 Гц. Ради вычислительных удобств при построении графика спектра примемf_д= 70 Гц.

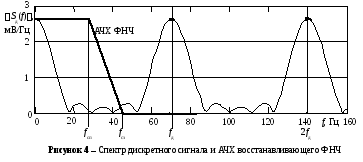
Строим график спектральной плотности S (f) для положительных и отрицательных частот путем нанесения точек графика рис. 2 – это будет составляющая ряда сn= 0. Затем строим два сдвинутых вправо наf_ди 2f_дграфика – это будут составляющие ряда сn= 1 иn= 2. Амплитудный спектр дискретного сигнала рассчитывается как модуль суммы значений трех графиков. Расчеты проводятся для области 0f2f_д. Результаты расчетаS_д(f)приведены на рис. 4 (без учета множителяf_д). Там же показана АЧХ ФНЧ, который используется для восстановления непрерывного сигнала по отсчетам (масштаб для значений АЧХ не приводится). Его параметры – граничные частоты полосы пропусканияf_ппи полосы задерживанияf_пз. Эти параметры выбираются при условиях:f_ппF_max,f_пзf_д – F_max. На рис. 4 параметры выбраны из равенств:f_пп=F_max=27 Гц,f_пз=f_д – F_max= 43 Гц.

Представление непрерывного сигнала цифровым сигналом

Схема аналого-цифрового преобразователя (АЦП) должна содержать дискретизатор, квантователь и кодер отсчетов, а схема цифроаналогового преобразователя (ЦАП) – декодер и ФНЧ. Описание преобразований сигналов в АЦП и ЦАП можно найти в [1, разд. 2.9].

Для представления непрерывного сигнала цифровым сигналом необходимо выполнить квантование отсчетов s(kT_д) и кодирование их двоичным кодом. В результате равномерного квантования квантованные отсчетыs_кв(kT_д) принимают лишь значения, кратные шагу квантованияs:s_кв(kT_д) =p(kT_д)s, гдеp(kT_д) – целое число, уровень квантования. Квантование заключается в замене отсчетаs(kT_д) ближайшим квантованным значением s_кв(kT_д), которое однозначно описывается числомp(kT_д). Через такое приближенное представление отсчетов возникает погрешность квантования_кв(kT_д) =s_кв(kT_д) –s(kT_д). Ее значение по модулю не превышает половины шага квантования:_кв(kT_д)s/2. Расчет уровней квантования выполняется по соотношению

p(kT_д) =, где int (х)– целая часть отх.

Кодирование уровней квантования состоит в записи p(kT_д) в двоичной системе счисления. Код должен быть равномерным, т.е. все кодовые комбинации должны иметь одинаковое количество двоичных символов. Длина кода АЦПnопределяется как наименьшее целое 2ⁿ L, где– количество уровней квантования;s_max(t) иs_min(t) – возможные соответственно максимальное и минимальное значения сигналаs(t)^.

Длительность двоичного символа определяется простым соотношением Т_б=T_д/n. Для наглядности цифровой сигнал необходимо представить временной диаграммой.

Пример 7.Выполним квантование рассчитанных в примере 6 отсчетов при условии, что шаг квантованияs= 2 мВ, и кодирование уровней квантования. Анализируемый сигналs(t), имеетs_max(t) = 50 мВ иs_min(t) = 0, откуда= 25.

Из условия 2ⁿ Lдлина кодаn= 5.

Результаты расчетов приведены в табл. 3.

На рис. 5 представлена соответствующая временная диаграмма цифрового сигнала.

Длительность двоичного символа Т_б=T_д/n = 14/5 = 2,8 мс.

	0	1	1	0	1	1	0	1	1	0	1	1	0	0	1	1	0	1	1	0	0	1	1	0	1

–2Т_дТ_д0Т_д2Т_д3Т_д

Рисунок 5 –Временная диаграмма цифрового сигнала