8

Министерство образования и науки, молодежи и спорта Украины

Одесская национальная морская академия

Кафедра физики и химии

Лабораторная работа № 5-6

Определение отношения заряда электрона к его массе

УКАЗАНИЯ К ЛАБОРАТОРНОМУ ПРАКТИКУМУ

Составили: В.И. Михайленко,

А.А.Горюк,

Ф.А.Птащенко

Утверждено на заседании кафедры,

протокол № 2 от 29 сентября 2011 г.

Одесса 2011

Лабораторная работа № 5.6 определение отношения заряда электрона к его массе

1. Теоретическая часть

1.1. Введение

Материальным носителем наименьшего электрического заряда в природе является электрон. Его открыл Дж. Дж. Томпсон в 1897 г. Одной из важных характеристик электрона является удельный заряд, который равняется отношению заряда электрона е к его массе m. Существует несколько экспериментальных методов определения е/m. Одним из наиболее распространенных является метод „скрещенных полей”.

1.1. Сила Лоренца

Сила Лоренца – это сила, с которой магнитное поле действует на подвижный электрический заряд

,

(1)

где – индукция магнитного поля (его силовая характеристика),

– величина электрического заряда, на который действует сила Лоренца,

– скорость заряда,

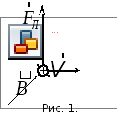
– угол между векторами и . В векторном виде, , т.е. сила Лоренца перпендикулярна векторам и . Ее направление определяется по правилу левой руки: если четыре пальца левой руки расположить параллельно направлению скорости положительного заряда, а линии индукции магнитного поля входят в ладонь, то отогнутый на 90^в большой палец будет показывать направление силы Лоренца – рис. 1. (На отрицательный заряд сила Лоренца будет действовать в противоположном направлении). Если скорость параллельна вектору , т.е.угол (рис. 2а), сила Лоренца равняется нулю. Когда (рис. 2б), сила Лоренца перпендикулярна скорости и вызывает центростремительное ускорение – заряд движется по окружности. Если скорость заряда образует угол с вектором (рис. 2в), сила Лоренца действует только на составляющую , перпендикулярную индукции магнитного поля. Тогда заряд движется по винтовой линии, ось которой параллельна вектору (составляющая скорости сохраняется, не меняет свое направление).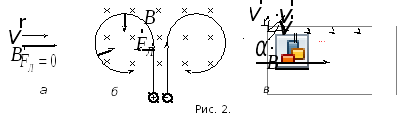

1.3. Метод скрещенных полей

В данном методе для определения отношения исследуется движение электрона во взаимно перпендикулярных электрическом и магнитном полях. Рассмотрим подробнее предложенный метод.

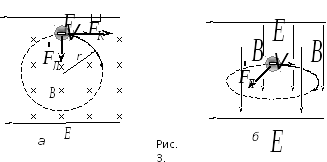
Как показано на рис. 3а, б, на подвижный электрон одновременно действуют скрещенные электрическое поле с напряженностью , и магнитное поле с индукцией , причем (на рис.3а направление вектора магнитная индукция обозначено символом „ ”, т.е. вектор перпендикулярный плоскости рисунка и направленный от нас). Электрическое и магнитное поля на электрон действуют независимо, и результат этого действия разный. В электрическом поле электрон будет ускоряться, поскольку на него действует кулоновская (электрическая) сила . Ее направление противоположно направления вектора (поскольку электрон несет отрицательный заряд). При перемещении электрона электрическое поле выполняет работу, которая равняется (где – разность потенциалов, которую прошел электрон, – заряд электрона). Именно за счет этой работы электрон будет приобретать кинетическую энергию , то есть:

(2)

В магнитном поле на электрон действует сила Лоренца, величина которой определяется выражением (1). Снова подчеркнем, что сила Лоренца действует только на подвижный заряд и всегда перпендикулярна к его скорости и, следовательно, не может выполнять работу, т.е. менять кинетическую энергию заряда. Единый результат влияния силы Лоренца на подвижную заряженную частицу состоит в изменении направления ее скорости.

В методе скрещенных полей магнитное поле однородное (B=const) и (). В этом случае электрон будет двигаться по дуге окружности радиусом r (рис. 3а), т.е. сила Лоренца играет роль центростремительной силы.

(3)

Приравнивая , получим

(4)

Подставив значение v из (4) в (2), получим выражение для e/m:

(5)