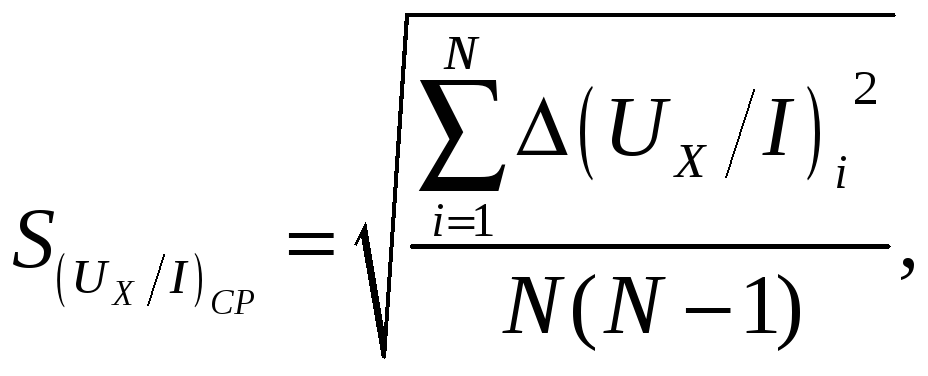7

Министерство образования и науки, молодёжи и спорта Украины

Одесская национальная морская академия

Кафедра физики и химии

Лабораторная работа № 5-5

Определение концентрации носителей заряда с помощью эффекта Холла

УКАЗАНИЯ К ЛАБОРАТОРНОМУ ПРАКТИКУМУ

Составили: В.И. Михайленко,

А.А.Горюк,

Ф.А.Птащенко

Утверждено на заседании кафедры,

протокол № 2 от 29 сентября 2011 г.

Одесса – 2011

Лабораторная работа № 5.5

ОПРЕДЕЛЕНИЕ КОНЦЕНТРАЦИИ НОСИТЕЛЕЙ ЗАРЯДА

С ПОМОЩЬЮ ЭФФЕКТА ХОЛЛА

1. Теоретическая часть

1.1. Сила Лоренца

Сила Лоренца – это сила, с которой магнитное поле действует на подвижный электрический заряд:

,

(1)

где – индукция магнитного поля ( его силовая характеристика),

– величина электрического заряда, на который действует сила Лоренца,

– скорость заряда,

– угол между векторами и . В векторном виде, , т.е. сила Лоренца перпендикулярна к и . Ее направление определяется по правилу левой руки: если четыре пальца левой руки разместить в направлении вектора скорости положительного заряда так, чтобы линии индукции магнитного поля входили в ладонь, то отогнутый на 90⁰ большой палец будет показывать направление силы Лоренца – рис. 1. (На отрицательный заряд сила Лоренца будет действовать в противоположном направлении). Если скорость параллельна вектору , т.е. угол (рис. 2а), сила Лоренца равняется нулю. Когда (рис. 2б), сила Лоренца перпендикулярна скорости и вызывает центростремительное ускорение – заряд движется по окружности. Когда скорость заряда образует угол с вектором (рис. 2в), сила Лоренца действует только на составляющую , перпендикулярную индукции магнитного поля. Тогда заряд движется по винтовой линии, ось которой параллельна вектору (составляющая скорости сохраняется, не меняет свое направление).

1.2. Эффект Холла

Эффект Холла состоит в следующем: Если металлическую или полупроводниковую пластинку с током поместить в магнитное поле так, чтобы вектор плотности тока был перпендикулярным линиям индукции магнитного поля , то на гранях пластинки, параллельных векторам и возникает поперечная разность потенциалов .

Объясним этот эффект. На рис. 3а изображена пластинка, через которую течет ток . Пусть это полупроводниковая пластинка, в которой носители заряда – положительные (дырки). Пластинка помещена в магнитное поле , линии индукции которого перпендикулярны плоскости рисунка и направлены от нас (обозначенные „ ”). На положительный заряд, который движется в направлении тока, в магнитном поле действует сила Лоренца. Ее направление определяется по правилу левой руки – на рисунке она направлена вверх. Под действием этой силы положительные заряды скапливаются на верхний грани пластинки, а нижняя грань заряжается отрицательно. Таким образом, между верхней и нижней гранями пластинки (между „плюсом” и „ минусом”) образуется разность потенциалов.

Если носителями заряда являются электроны, которые несут отрицатенльный заряд (например, в металлической пластинке, рис. 1б), то на верхней грани будет скапливаться отрицательный заряд, а на нижний – положительный, т.е. направление холловской разности потенциалов будет противоположным.

Найдем величину холловской разности потенциалов. Пусть носители заряда в пластинке – положительные (рис. 4). При протекании тока ( с плотностью тока ) заряды движутся со скоростью . В магнитном поле с индукцией на каждый из них действует сила Лоренца

(2)

(поскольку угол между векторами и равняется 90⁰, ). Сила Лоренца отклоняет положительные заряды к верхней грани пластинки, а на нижней грани скапливается отрицательный заряд. Это служит причиной появления поперечного электрического поля , направленного сверху вниз ( от „+” к „–”). Связанная с этим полем сила кулоновского отталкивания

(3)

направленна также вниз (противоположно силе Лоренца), она препятствует дальнейшему накоплению зарядов на гранях пластинки. В стационарном состоянии кулоновская сила компенсирует силу Лоренца

(4)

Напряженность однородного электрического поля связана с разностью потенциалов между верхней и нижней гранями соотношением

,

(5)

где называют холловская разность потенциалов;

d – толщина пластинки (рис. 4).

П лотность тока связана со скоростью направленного движения зарядов и их концентрацией соотношением

,

(6)

откуда скорость зарядов равняется

.

(7)

Подставим (7) в (4)

,

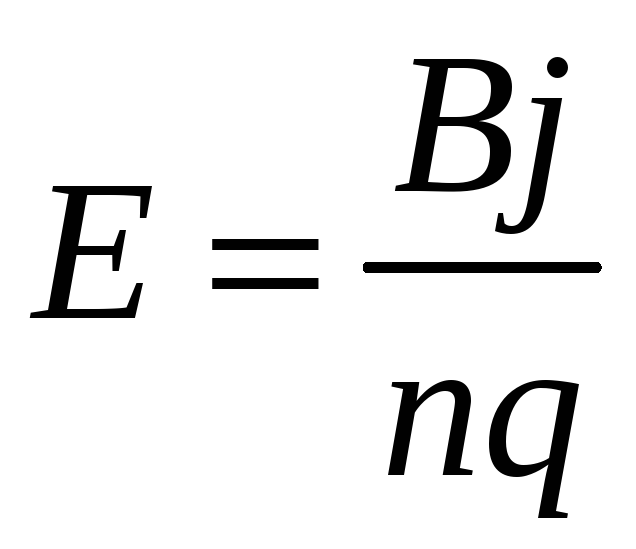и далее полученное выражение в (5), В результате получим выражение для холловской разности потенциалов:

(8)

Плотность тока равняется отношению силы тока к площади поперечного сечения проводника:

,

(9)

где – ширина пластинки. Учитывая (9), холловскую разность потенциалов можно представить в виде

(10)

Величина

(11)

называется постоянной Холла, значение которой зависит от природы вещества, а знак совпадает со знаком носителей заряда. Более строгие расчеты показывают, что для полупроводников постоянная Холла равна

(12)

Эффект Холла имеет ряд разных применений. Так датчики Холла используют для измерения магнитных полей (U_Х ~В). С их помощью можно дистанционно измерять силу тока в высоковольтных линиях электропередач и находить электрические провода в стенах зданий. Постоянная Холла дает возможность установить знак носителей заряда в данном веществе и определить их концентрацию.

2. Экспериментальная часть

2.1. Цель работы

Вычислить постоянную Холла и концентрацию носителей заряда.

2.2. Приборы и оборудование

Холловская пластинка, источник постоянного тока , реостат , миллиамперметр, магазин сопротивлений , милливольтметр, электромагнит.

П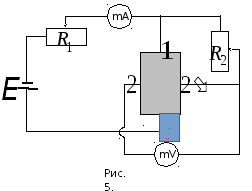ринципиальную схему установки для измерения ЭДС Холла при постоянном токе, который течет через пластинку, показано на рис. 5. К пластинке присоединены две пары электродов, одна из которых (1-1^/) подводит к ней ток, а вторая (2-2^/) представляет собой зонды для снятия U_Х . На пластинку подается постоянный ток, величина которого регулируется реостатом и измеряется миллиамперметром mА. Милливольтметр mV фиксирует холловскую разность потенциалов U_Х.

При протекании тока через пластинку на холловских электродах может возникнуть паразитное напряжение и при отсутствии магнитного поля. Она вносит погрешность при определении холловской разности потенциалов. Наличие паразитного напряжения объясняется неэквипотенциальностью (несимметричностью) холловских электродов. Для исключения этой погрешности один из холловских электродов подключен к источнику тока через переменное сопротивление , подбором величины которого можно выровнять потенциалы электродов 2 и 2^/ .

2.3. Порядок проведения измерений

Для заданных руководителем значений силы тока в пластинке выполнить 8-10 измерений холловской разности потенциалов – U_Х. При этом, при отключенном магнитном поле подбором сопротивления , ликвидируют паразитное напряжение на холловских электродах для каждого значения силы тока . Результаты измерений заносят в таблицу.

Таблица.

B=……мм В=……Тл

№	I, mА	UХ, mВ
1. 2. . . . 10.

2.4. Обработка результатов измерений

1. Постройте график U_Х =f(I), (рис. 6).

2. Выберите на прямой две точки А и В с координатами (I_А , ) и (I_В , ) и вычислите коэффициент β:

. (13)

3. В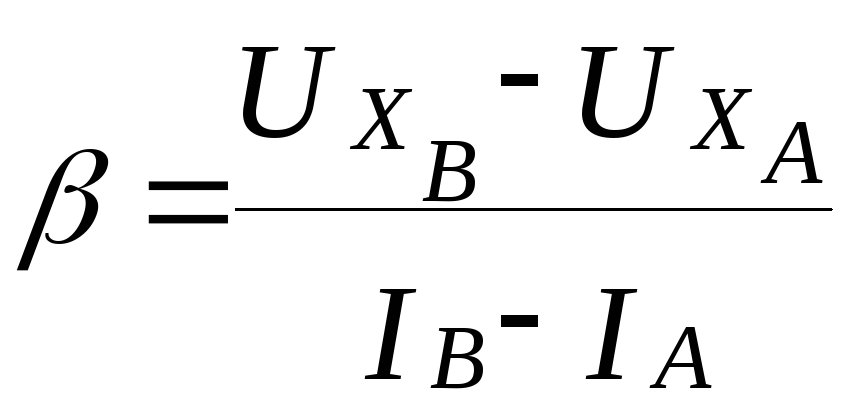ычислите постоянную Холла: из (10) следует . Тогда среднее значение постоянной Холла будет равняться:

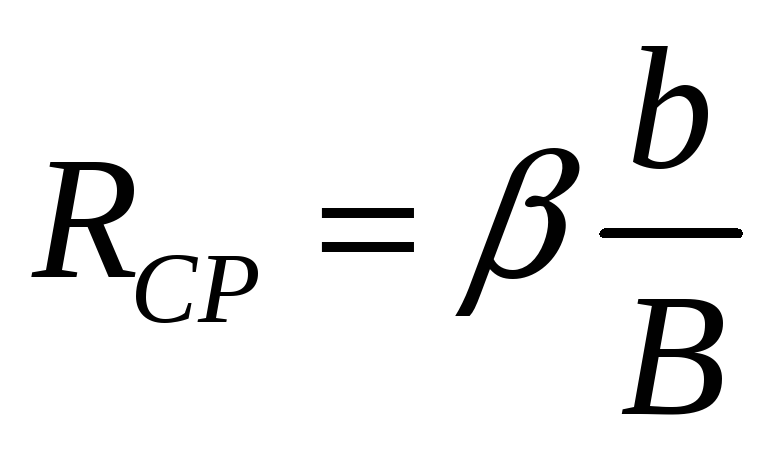
   (14)

4. Найдите концентрацию носителей

,

(15)

где q = 1,6·10^-19 Кл – элементарный заряд.

Постоянная Холла измеряется в м ³/Кл; концентрация n - в м^–3. Погрешности R и n определяются формулами

,	(16)
,	(17)

где

(18)

а – число измерений.

5. Результат записать в виде:

	(19)
	(20)

Контрольные вопросы

1. Чему равняется сила Лоренца? Как она направлена?

2. По каким траекториям могут двигаться заряды под действием силы Лоренца?

3. В чем состоит эффект Холла? Объясните его механизм, нарисуйте схему (рис. 4).

4. Выведите выражение для холловской разности потенциалов.

5. Где практически применяют эффект Холла?

6. По каким формулам вычисляют постоянную Холла и концентрацию носителей заряда?

ЛИТЕРАТУРА

1. В.И.Михайленко, В. Г.Белоус, Ю.М.Поповский. Общая физика, 1994. - с.226-228.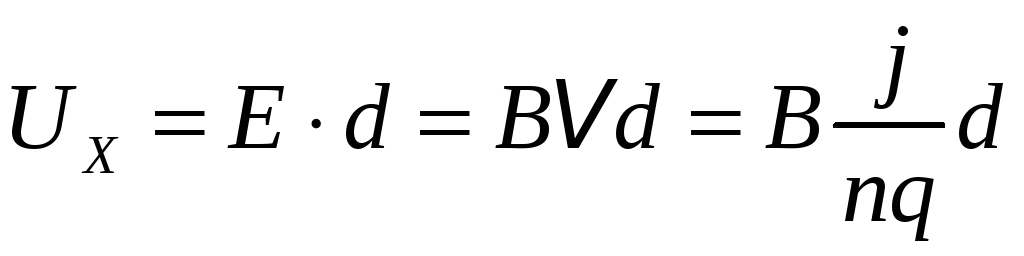
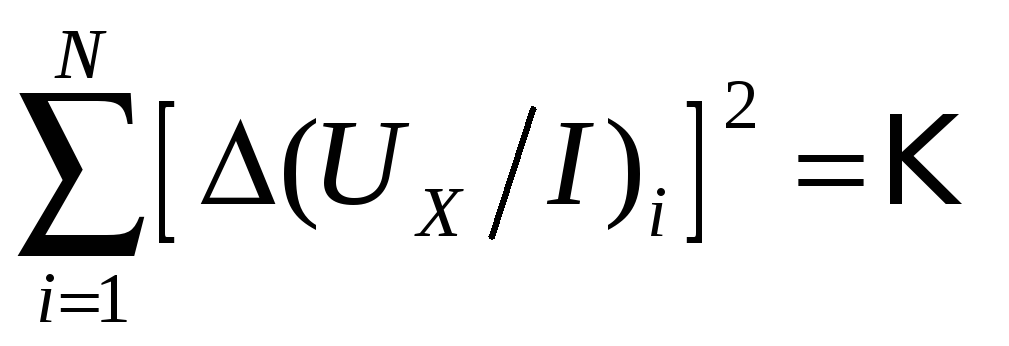
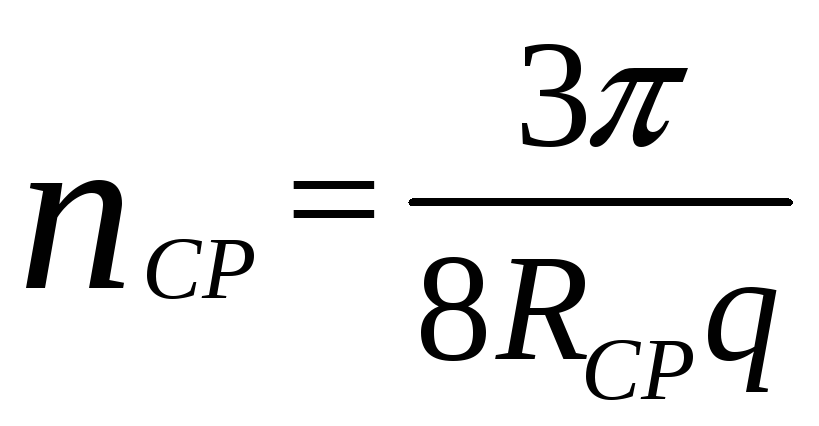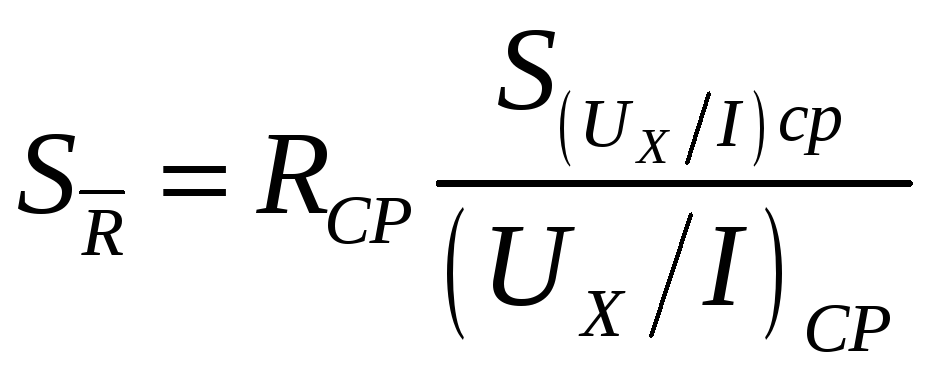