1.2. Зависимость полезной мощности источника электрического тока от силы тока и внешнего сопротивления

Рассмотрим электрическую цепь, состоящую из источника постоянного тока и внешнего сопротивления R (рис. 1). При протекании тока через такую цепь источником ЭДС выполняется работа и в цепи выделяется мощность.

П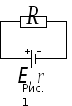олезной мощностью называют мощность, которая выделяется на внешнем сопротивлении. Из закона Джоуля-Ленца (10*) полезная мощность равняется , а из закона Ома для участка цепи. Тогда полезная мощность будет

,

(1)

где – падение напряжения на внешнем сопротивлении. При протекании тока по цепи также выделяется „бесполезная” мощность – разогревается источник ЭДС. По закону Джоуля-Ленца эта мощность равняется. Полная мощность, которая выделяется во всей цепи, равняется. Используя закон Ома для полной цепи, можно найти полную мощность

.

(2)

Итак, полная мощность, которая выделяется в цепи, равняется произведению силы тока на ЭДС источника тока.

Пусть в цепи можно менять внешнее сопротивление . Проанализируем, как полезная и полная мощности зависят от силы тока и внешнего сопротивления.

Полезная мощность равняется разности между полной мощностью и „бесполезной”:

.

(3)

Рис. 2

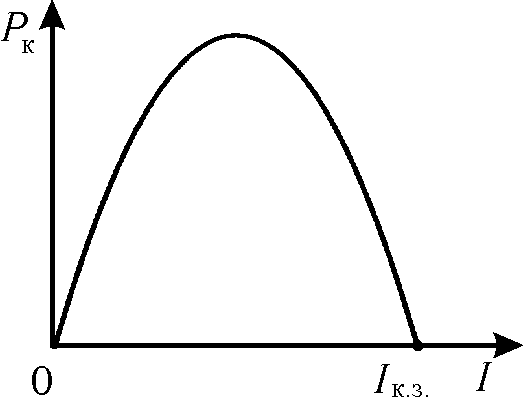
Из этого выражения видно, что полезная мощность является квадратичной функцией силы тока I. График этой функции будет представлять собой параболу (рис. 2).

Из рис. 2 вытекает, что в двух случаях:

• когда цепь разомкнута (R = ∞), то сила тока в цепи I = 0;

• когда возникло короткое заключение, при этом R = 0, а сила тока в цепи будет максимальной .

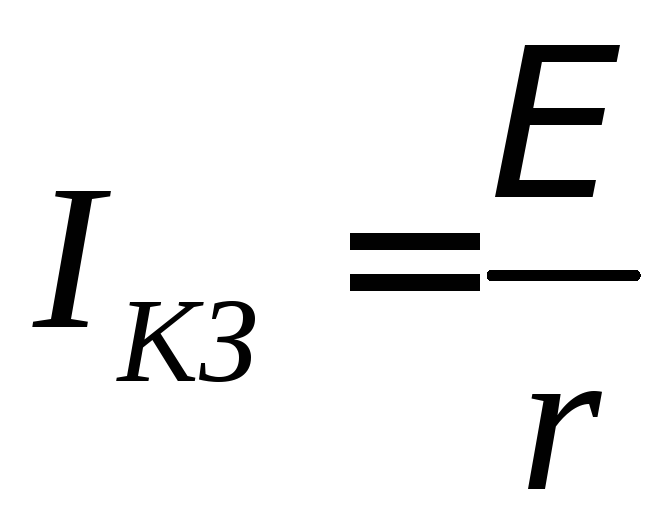Меняя величину внешнего сопротивления, можно достичь некоторого значения силы тока в цепи, при котором полезная мощность будет максимальной. Найдем этот ток. Для этого найдем первую производную и приравняем ее нулю. Из выражения (3) имеем:

.

(4)

Отсюда вытекает

,

(5)

а ток , при котором выделяется максимальная полезная мощность, равняется. С другой стороны, на основании закона Ома для полной цепи, где– сопротивление, при котором выделяется максимальная полезная мощность. Приравнивая два последних выражения, находим, что

.

(6)

Таким образом, полезная мощность будет максимальной при условии равенства внешнего и внутреннего сопротивлений.

Зависимость полезной мощности от внешнего сопротивления можно найти из закона Джоуля-Ленца и закона Ома для полной цепи

.

(7)

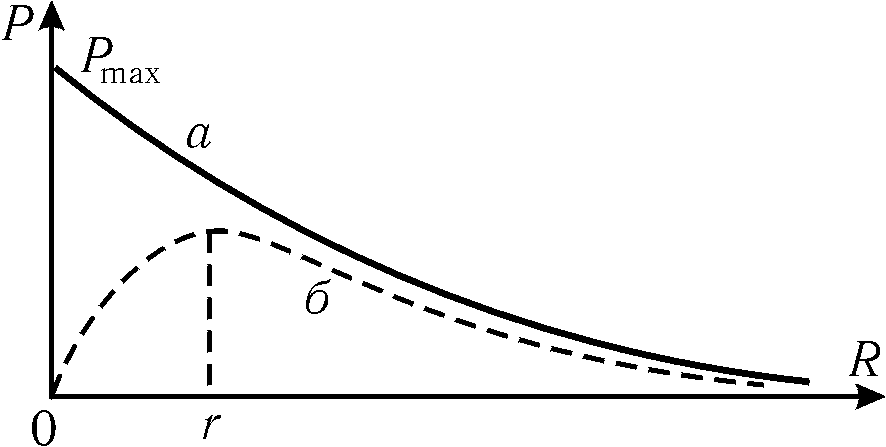
График зависимости показан на рис. 3 (криваяб). Максимум функции можно найти, приравниваянулю

.

(8)

Из (8) также вытекает ожидаемое равенство .

а – полная мощность

б – корисна потужність

Рис. 3

Рассмотрим теперь, как полная мощность зависит от внешнего сопротивления. Используя выражение (2) и закон Ома для полной цепи находим зависимость полной мощности от внешнего сопротивления:

. (9)

График этой зависимости показана на рис. 3 (кривая а). При изменении внешнего сопротивления от нуля (короткое заключение) до бесконечности (цепь разомкнута) полная мощность будет убывать от максимального значения до нуля.

3. Зависимость коэффициента полезного действия источника электрического тока от силы тока и внешнего сопротивления цепи

Коэффициент полезного действия (КПД) равняется отношению полезной мощности (1) к полной мощности (2), которая выделяется во всей цепи

(10)

Сначала найдем зависимость КПД от силы тока. Если разделить выражение (3) для полезной мощности на выражение (1) для полной мощности, получим

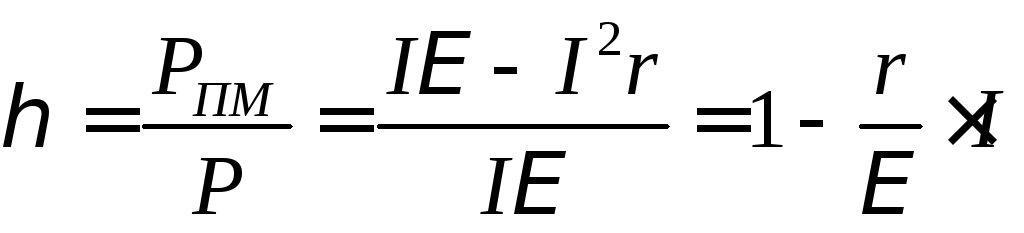(11)

Итак, КПД представляет собой линейную функцию от силы тока (рис. 4). Когда I → 0 (цепь разомкнут), то . При коротком заключении, ток короткого заключения

(12)

и КПД будет .

Чтобы найти зависимость КПД от внешнего сопротивления, подставим в (9) выражение для из закона Ома для участки цепи, а выражение для– из закона Ома для полной цепи. Тогда

.

(13)

Из соотношения (13) вытекает:

• при R ® 0 (короткое заключение, );

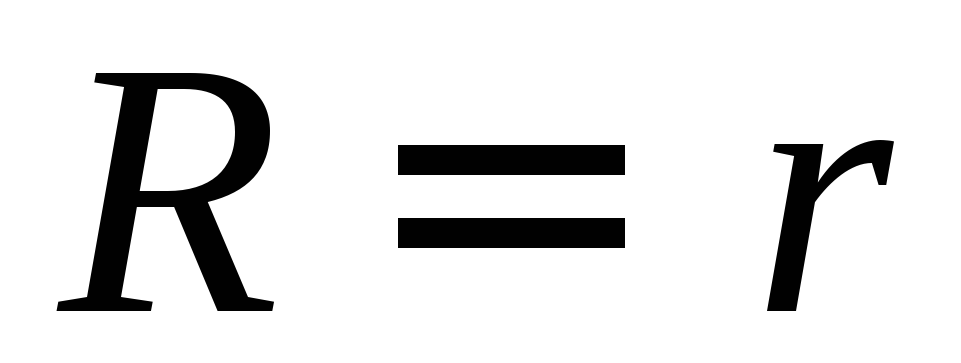• при R ® ¥ ( цепь разомкнут, );

• при R = r (условие максимума полезной мощности) .

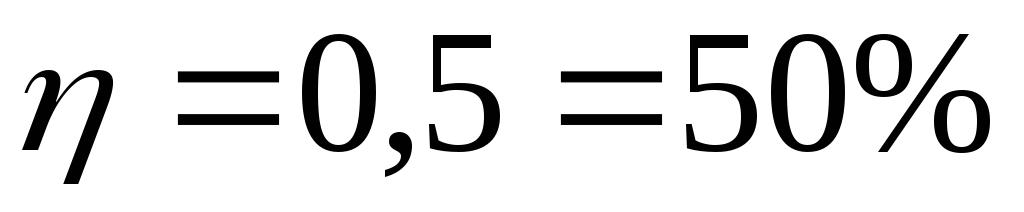Приведенный анализ показывает, что при увеличении внешнего сопротивления КПД асимптотично приближается к единице (рис. 5).
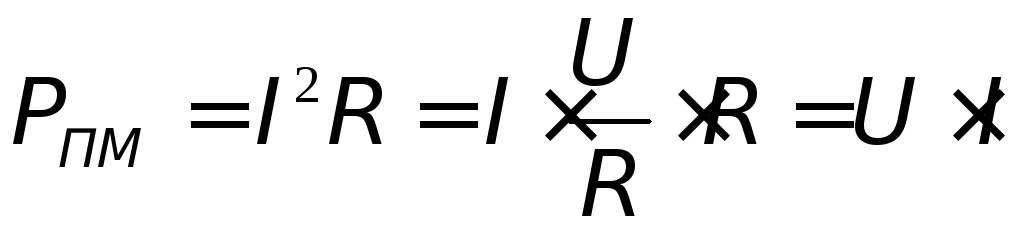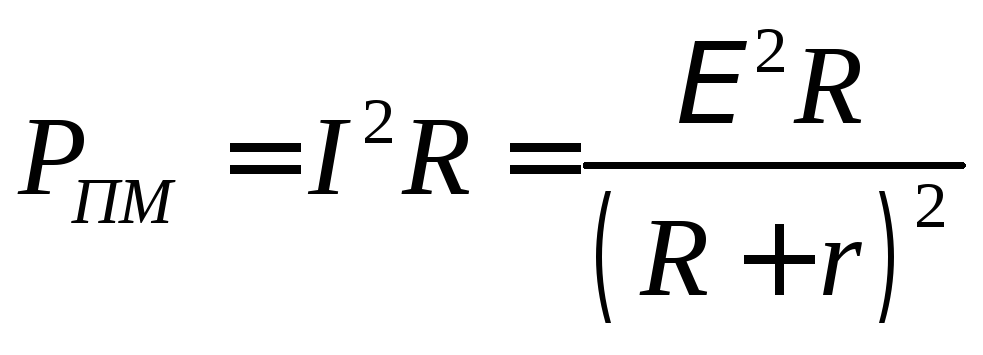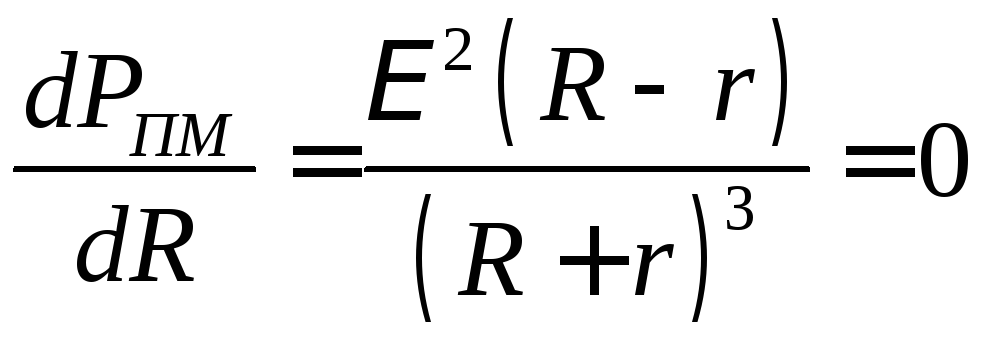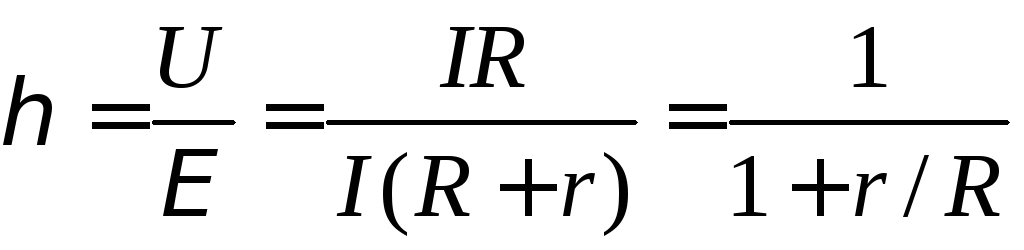