2.Расчёт водоизмещения (массы) и координат цт.

Исходные данные для расчета нагрузки судна, т.е. массы судна, и координат его центра тяжести содержатся в грузовом плане судна, в котором приводится распределение перевозимых грузов и судовых запасов по грузовым помещениям и цистернам с ука­занием массы в каждом из них. Масса и координаты ЦТ судна порожнем указаны в судовом документе «Информация об остой­чивости судна». Там же приводится форма таблицы, рекомендуе­мой для расчета нагрузки судна (табл.).

Расчет нагрузки (перевозимый груз)

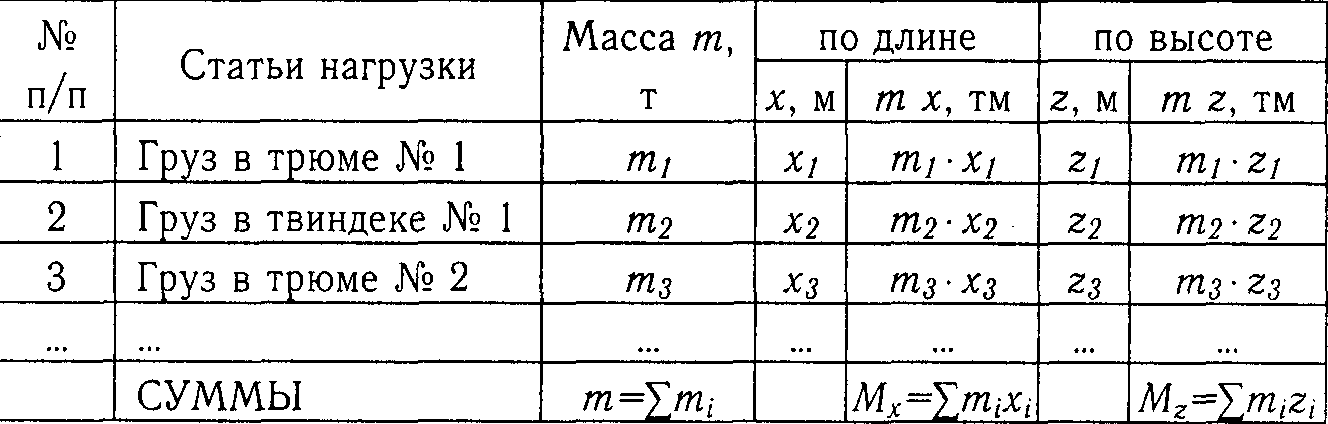
Ввиду того, что расчет нагрузки требуется производить для случаев как в полном грузу, так и при израсходованных запасах (обычно с 10% запасов), соответствующих началу и концу рейса, целесообразно составлять таблицы нагрузки отдельно для судо­вых запасов, расходуемых в рейсе, и для перевозимого груза, а затем составить сводные таблицы для разных состояний нагрузки судна.

В столбце 2 таблицы перечисляются все принятые к перевоз­ке грузы, в столбцах 3, 4 и 6 — соответственно их массы и координаты центров тяжести по длине от миделя и по высоте от основной плоскости. В столбцах 5 и 7 вычисляются статичес­кие моменты масс относительно тех же координатных плоско­стей. Грузы, расположенные в нос от миделя, имеют положитель­ные х и mх, расположенные в корму от миделя — отрицательные. Если в одно грузовое помещение принимается несколько различ­ных грузов, то каждый из них заносится в таблицу нагрузки отдельной строкой.

Моменты масс по ширине судна как правило не рассчитывают­ся, так как грузы укладываются симметрично относительно диа­метральной плоскости и для них y_i = 0. Во всяком случае, сум­марный момент M_y от несимметрично принятых грузов должен быть достаточно малым, чтобы не было заметного угла крена, который недопустим при нормальной эксплуатации.

Таблицы нагрузки, содержащие судовые расходуемые запасы, и сводная таблица имеют ту же форму, что и табл. 2.1, но состав­ляются в двух вариантах — на начало и конец рейса, а в некото­рых случаях и для промежуточного состояния нагрузки. После суммирования сводной таблицы по столбцам 3, 5 и 7 искомые величины для каждого состояния нагрузки определяются по фор­мулам:

где N — число статей нагрузки, составляющих дедвейт судна.

Если водоизмещение судна порожнем D₀ и его статические моменты D₀х_g0 и D₀z_g0 вносятся в качестве первой строки в табл. 2.1, то первые слагаемые в формулах (2.16) войдут в итоговые суммы и выражения (2.16) примут вид:

3.Остойчивость на больших углах крена. Диаграмма статической остойчивости. Особенности диаграммы.

При больших наклонениях моменты инерции равнообъемных ватерлиний изменяются с углом крена. Соответственно изменя­ются и радиусы кривизны траектории центра величины, которая будет отличаться от окружности, положенной в основу при выво­де метацентрической формулы остойчивости. Указанное обстоя­тельство существенно меняет зависимость восстанавливающего момента от угла крена. Установление этой зависимости и являет­ся первой задачей при изучении остойчивости при больших углах крена.

Если кренящая пара наклоняет судно на большой угол, то траектория центра величины не лежит в поперечной плоскости. Вследствие несимметрии носовой и кормовой оконечностей появ­ляется смещение центра величины в продольном направлении и пара, образуемая весом судна и силой поддержания, не будет совпадать с плоскостью кренящей пары. Разлагая образующуюся пару на составляющие в поперечной и продольной плоскостях, получим, что поперечная составляющая уравновесит кренящую пару, а продольная вызовет наклонение судна в продольном на­правлении. Момент этой продольной составляющей пары назы­вается деривационным моментом. При обычной форме обводов дифферент, вызванный деривационным моментом, оказывается малым, им пренебрегают и рассматривают не действительную пространственную траекторию центра величины, а ее проекцию на плоскость наклонения. Эта проекция траектории ЦВ называет­ся кривой центра величины (кривой С).

ДСО. Зависимость плеча восстанав­ливающего момента от угла крена изображают в прямоугольных координатах, откладывая по оси абсцисс углы крена в градусах, а по оси ординат — плечи остойчивости в метрах. Кривая, пред­ставляющая эту зависимость, называется диаграммой статичес­кой остойчивости или диаграммой Рида. Поскольку диаграмма строится для постоянного водоизмещения, она же изображает зависимость восстанавливающего момента от угла крена, для чего масштаб момента можно также нанести на оси орди­нат. Диаграмма статической остойчивости изображена на рис. 4.5.

Ввиду симметрии формы судна диаграмма строится только для положительных углов крена (на правый борт). При крене на противоположный борт (ϴ<0) диаграмма продолжается как не­четная функция:

Характерными параметрами диаграммы являются: крутизна начального участка, максимальное плечо остойчивости lmах, угол максимума диаграммы ϴт, угол заката диаграммы ϴv (при котором плечо остойчивости обращается в нуль), площадь, ограниченная кривой и осью абсцисс. Эти параметры характеризуют остойчи­вость на больших углах крена.