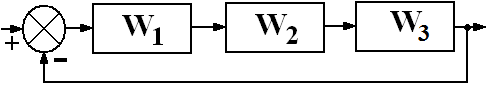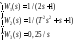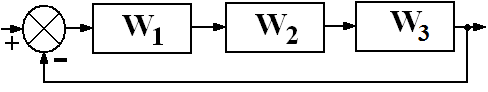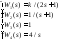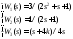5.3. Выполнение работы

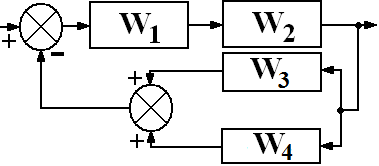
В соответствии со своим номером n в академическом журнале курсант должен из табл. 5.2 выбрать вариант задания, в котором указан вид структурной схемы задачи и заданы значения передаточных функций звеньев.

Таблица 5.2. – Структурная схема САУ и передаточные функции звеньев

n	Структурная схема	Передаточные функции	n	Структурная схема	Передаточные функции
1	2	3	4	5	6
1			13
2			14
3			15
4			16
Продолжение таблицы 6.2
1	2	3	4	5	6
5			17
6			18
7			19
8			20
9			21
10			22
11			23
12			24

5.3.1. Определение границы устойчивости линейной системы без транспортного запаздывания

При выполнении этой части работы следует придерживаться следующего порядка действий:

1. Составить выражение для передаточной функции замкнутой системы и выделить знаменатель полученного выражения.

2. В соответствии с критерием Гурвица составить соответствующий определитель и получить неравенство, включающее в себя в качестве неизвестного значение варьируемого параметра.

3. Решить уравнение и определить критическое значение варьируемого коэффициента, отвечающего выходу исследуемой системы на границу колебательной устойчивости.

4. Составить схему S-модели, соответствующей заданной структурной схеме. Установить найденное значение в окне свойств соответствующего блока схемы. Проверить, что система настроенная таким образом будет находиться на границе устойчивости – с этой целью провести расчет переходного процесса и убедиться, что он представляет собой незатухающие гармонические колебания.

Пункты 1-3 могут быть выполнены как вручную, так и с помощью одного из пакетов компьютерной математики, которые обладают возможностями аналитических преобразований.

5.3.2. Методический пример выполнения

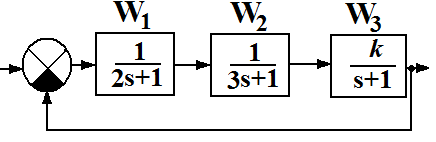
Пусть изучается устойчивость системы, структурная схема которой представлена на рис.5.3, а значения передаточных функций указаны внутри блоков.

Рис.5.3. Пример структурной схемы системы исследуемой на устойчивость.

Составим выражение для передаточной функции замкнутой системы:

;

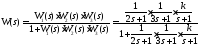Свернем и упростим это выражение, используя следующий набор команд:

>> syms s k; %Указание символьных переменных задачи

>> w1=1/(2*s+1);w2=1/(3*s+1);w3=k/(s+1); % определение передаточных функций звеньев;

>> w=w1*w2*w3/(1+w1*w2*w3); % формула передаточной функции замкнутой системы;

>> W=simplify(w)

W =

k/(5*s^3+11*s^2+5*s+1+k)

Для системы 3 порядка критерий Гурвица сводится к проверке выполнения условия Вышнеградского. В случае систем более высоких порядков рационально составить матрицу Гурвица, исключением строк и столбцов сформировать соответствующий диагональный минор и вычислить его детерминант. Затем, приравняв его к нулю (условие нахождения системы на границе колебательной устойчивости), решить полученное уравнение относительно входящего в него неизвестного варьируемого параметра. Данная процедура также может быть реализована как вручную, так и в рамках пакета компьютерной математики.

В данном примере к помощи компьютера прибегать нецелесообразно, поскольку система 3 порядка и условие устойчивости – это уравнение Вышнеградского, которое записывается в виде:

То есть критическое значение коэффициента усиления третьего звена, соответствующее границе устойчивости, равно 10.

Составим S-модель, соответствующую структурной схеме системы, представленной на рис. 5.3, и промоделируем переходной процесс, приняв . СхемаS-модели и результат моделирования представлены на рис. 3.4.

а	б
Рис. 5.4. S-модель системы на границе устойчивости (а) и результат моделирования переходного процесса (б).

Как видно из рис.5.4 критическое значение коэффициента усиления найдено верно, поскольку переходной процесс в системе соответствует незатухающему колебанию.