5.2 Експрес-аналіз функціонування комп’ютерних систем

5.2.1 Математичне очікування числа працездатних ем у системі

1. Стаціонарний режим – режим, при якому система тривало експлуатується.

Розрахунок здійснюється по формулі:

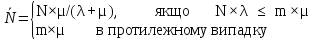. (5.17)

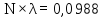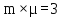У нашому випадку, , а , умова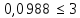виконується, тому розрахуємо математичне очікування числа у стаціонарному режимі по першій формулі:

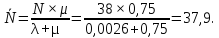(5.18)

2. Перехідний режим. Режим, при которому система тількі починає функціо-нувати. Розрахунок здійснюється по формулі:

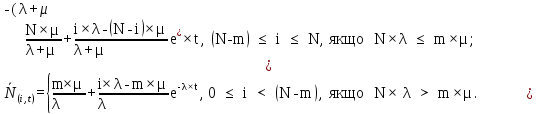(5.19)

Де ֪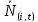– це число працездатних ЕМ тривалій експлуатації. Для розрахунку візьмемо і =36. Так як у нашому випадку 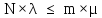, то розрахуємо функцію перехідного режиму в різних значеннях t, і занесем дані до таблиці (5.5):

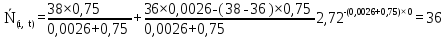
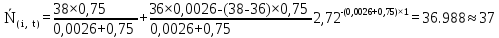
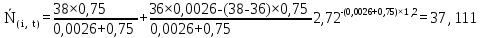
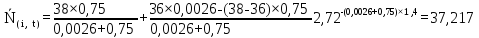
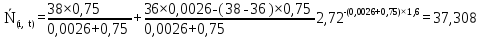
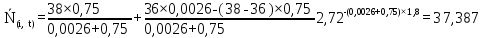
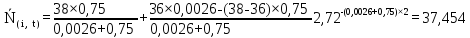
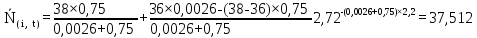
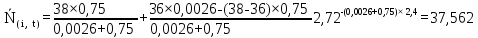
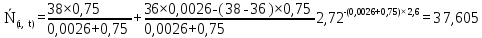
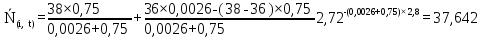
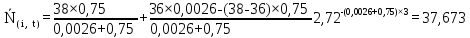
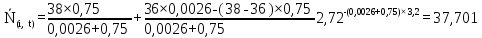
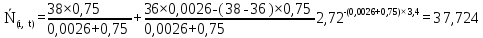
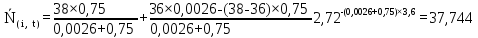
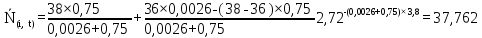
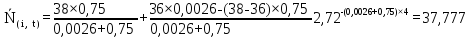
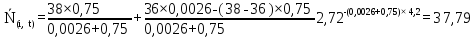
Рисунок 5.4 – Графік залежності N(i,t)

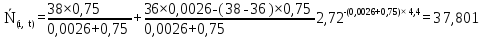
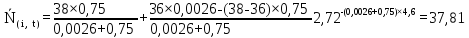
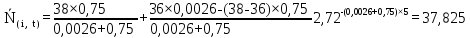
Таким чином, результати розрахунку функції перехідного режиму наведені у таблиці (5.5).

Таблиця 5.5 – Точки математичного очікування числа в перехідному режимі

t	0	1	1,2	1,4	1,6	1,8	2	2,2	2,4	2,6	2,8
N(i,t)	36	37	37,111	37,217	37,308	37,387	37,454	37,512	37,562	37,605	37,642
t	3	3,2	3,4	3,6	3,8	4	4,2	4,4	4,6	4,8	5
N(i,t)	37,673	37,701	37,724	37,744	37,762	37,777	37,79	37,801	37,81	37,818	37,825

Побудуємо графік залежності N(i,t)(Рисунок 5.4)

5.2.2 Функція здійснювання рішення завдання на живучій комп'ютер-ній системі

Під живучістю КС розуміється властивість программного настроювання й організації функціонування таких структурних схем, які в умовах відмов і відновлення обчислювачів гарантують при виконанні паралельної програми продуктиінсть у заданих межах або можливість використання всіх справних обчислювачів. Поняття живучості обчислюівальних систем характеризує їхньої здатності по оргазінації відмовостійких обчислень або, говорячи інакше, по реалізації паралельних программ, що допускають варіювання числа галузей у відомих межах.

Стаціонарний режим; F(t) – імовірність того, що на КС, що перебуває в тривалій експлуатації, буде вирішена за час 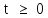завдання, представлене паралельною програмою, що адаптується, тобто програмо, що використовує в будь-який момент часу всі працездатні ЕМ. Розрахунок робиться по формулі:

(5.21)

Згідно з моїм варіантом, β = 7 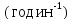. Виконаємо розрахунок по формулі (5.21) змінюючи значеннях t, і занесем дані до таблиці (5.6):

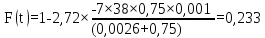
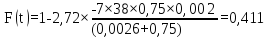
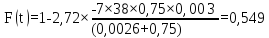
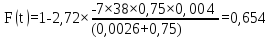
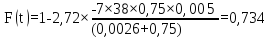
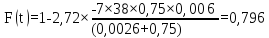
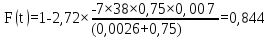
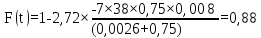
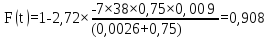
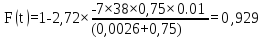
Таким чином, результати розрахунку функції перехідного режиму наведені у таблиці (5.6).

Таблиця 5.6 – Результати залежності F(t)

t	0	0,001	0,002	0,003	0,004	0,005	0,006	0,007	0,008	0,009	0.01
F(t)	0	0,233	0,411	0,549	0,654	0,734	0,796	0,844	0,88	0,908	0,929

Графік функції F(t) зображено у додатку Д.

Перехідний режим; F(i,t) – імовірність того, що на КС, що почала функціонувати в стані i, , буде за час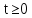вирішене завдання, представлене у вигляді паралельної програми, що адаптується. Розрахунок виконується по формулі:

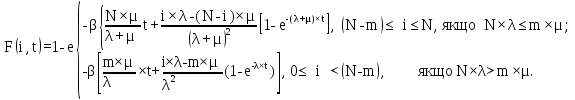(5.23)

Розрахуємо функцію F(i,t) по формулі (5.23), для різних значень t:

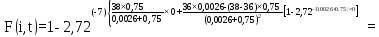0

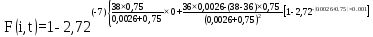=0,223

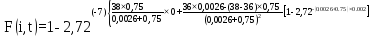=0,396

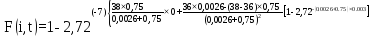=0,53

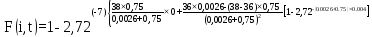=0,635

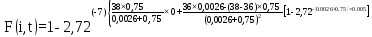=0,716

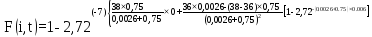=78

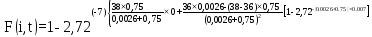=0,829

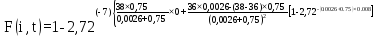=0,867

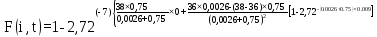=0,897

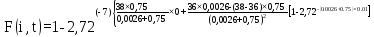=0,92

Таким чином, результати розрахунку функції перехідного режиму наведені у таблиці (5.7).

Таблиця 5.7 – Результати залежності F(i,t)

t	0	0,001	0,002	0,003	0,004	0,005	0,006	0,007	0,008	0,009	0.01
F(t)	0	0,223	0,396	0,53	0,635	0,716	0,78	0,829	0,867	0,897	0,92

Побудуємо графік функції F(i,t):

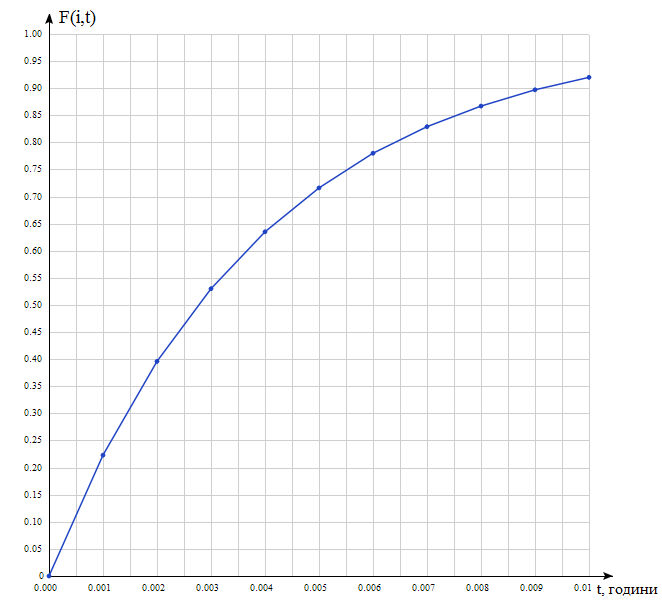
Рисунок 5.5 – Графік функції залежності F(i,t)