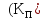- •Курсовий проект
- •Завдання
- •1 Класифікація комп’ютерних систем
- •2 Архітектура комп’ютерних систем
- •2.1 Різновиди архітектур комп’ютерних систем
- •2.2 Архітектура комп’ютерної системи микрос
- •3 Топологія комп’ютерних систем
- •3.1 Різновиди топологій комп’ютерних систем
- •3.2 Топологія типу «Дерево»
- •4 Закон амдаля і його застосування при створенні комп’ютерних систем
- •4.1 Теоретичні відомості
- •4.2 Розрахунок коефіцієнту прискорення
- •5 Розрахунок параметрів комп’ютерних систем
- •5.1 Розрахунок функції надійності комп’ютерних систем
- •5.2 Експрес-аналіз функціонування комп’ютерних систем
- •5.2.1 Математичне очікування числа працездатних ем у системі
- •5.2.2 Функція здійснювання рішення завдання на живучій комп'ютер-ній системі
- •Висновки
- •Також, розрухував функцію здійснювання рішення завдання на живучій комп'ютерній системі як для стаціонарного режиму, так і для перехідного режиму. Список використаних джерел
- •Додаток а – Класифікація комп’ютерної системи Базу
4.2 Розрахунок коефіцієнту прискорення
Коефіцієнт
прискорення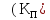 показує, у скільки разів швидше комп'ютерна
система вирішить завдання ніж один
обчислювач, а так само, у скільки разів
швидше буде вирішена задача при
використанні паралельного алгоритму
ніж без нього.
показує, у скільки разів швидше комп'ютерна
система вирішить завдання ніж один
обчислювач, а так само, у скільки разів
швидше буде вирішена задача при
використанні паралельного алгоритму
ніж без нього.
Розрахуємо коефіцієнт прискорення по формулі:
 ,
(4.6)
,
(4.6)
Нам
дано, що N=38.
Розрахуємо коефіцієнт прискорення,
змінюючи частку послідовних обчислень
f
від 0 до 1 з шагом 0,05. Виконаємо розрахунок
 :
:



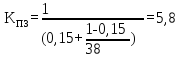







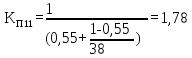









Таким чином, результати розрахунку коефіцієнту прискорення наведені у таблиці 4.1.
Таблиця
4.1 – Значення функції коефіцієнту
прискорення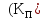 і аргументуf
і аргументуf
|
f |
0 |
0,05 |
0,1 |
0,15 |
0,2 |
0,25 |
0,3 |
0,35 |
0,4 |
0,45 |
0,5 |
|
|
38 |
13,3 |
8,1 |
5,8 |
4,52 |
3,7 |
3,14 |
2,72 |
2,4 |
2,15 |
1,95 |
|
f |
0,55 |
0,6 |
0,65 |
0,7 |
0,75 |
0,8 |
0,85 |
0,9 |
0,95 |
1 |
– |
|
|
1,78 |
1,63 |
1,52 |
1,41 |
1,32 |
1,24 |
1,17 |
1,11 |
1,05 |
1 |
– |
Графік
функції
 відf
зображено
в
додатку В.
відf
зображено
в
додатку В.
5 Розрахунок параметрів комп’ютерних систем
5.1 Розрахунок функції надійності комп’ютерних систем
Розрахунок параметрів комп’ютерної системи повинен вироблятися на основі наступних вихідних даних:
N – число елементарних машин, складових комп’ютерну систему;
ω – показник продуктивності однієї елементарної машини;
λ
– інтенсивність відмов елементарної
машини – середнє число відмов, що
відбуваються в однії елементарній
машині протягом 1 години ( ,
год, – середній наробіток до відмови
машини);
,
год, – середній наробіток до відмови
машини);
m
– число (віртуальних) пристроїв, що
відновлюють (ВП). Кожне ВП здатно
ремонтувати в будь-який момент t часу
тільки одну елементарну машину;
часу
тільки одну елементарну машину;
μ
– інтенсивність
відновлення елементарної машині –
середнє число відновлень машин, що може
зробити одне ВП за 1 годину ( ,
год, – середній час відновлення машини
одним ВП);
,
год, – середній час відновлення машини
одним ВП);
β
– інтенсивність
рішення завдання на одній елементарної
машині комп’ютерної системи ( ,
год, – середній час відновлення машини
одним ВП);
,
год, – середній час відновлення машини
одним ВП);
і – початковий стан комп’ютерної системи або число працездатних елементарних машин у момент початку функціонування системи, тобто при t = 0; {0, 1, … , N} – безліч станів комп’ютерної системи.
Надійність – властивість об'єкта виконувати задані функції, зберігаючи в часі значення встановлених експлуатаційних показників у заданих межах, що відповідають заданим режимам і умовам використання, технічного обслуговування, ремонтів, зберігання й транспортування.
Тут і далі, під поняттям «об’єкт» маємо на увазі або складові вузли компь’ютерної системи, або комп’ютерну систему, як окремий вибір, або програмний продукт для комп’ютерної системи.
Підвищення надійності засноване на принципі запобігання несправностей шляхом зниження інтенсивності відмов і збоїв за рахунок застосування електронних схем і компонентів з високим і надвисоким ступенем інтеграції, зниження рівня перешкод, полегшених режимів роботи схем, забезпечення теплових режимів їхньої роботи, а також за рахунок удосконалювання мето-дів складання апаратури.
Поняття надійності включає не тільки апаратні засоби, але й програмне забезпечення, що використовується, зокрема, для аналізу продуктивності систем
і керування конфігураціями.
Надійність є комплексною ластивістю, що включає в себе залежно від призначення об’єкта або умов його експлуатації ряд простих властивостей:
– безвідмовність;
– довговічність;
– ремонтопридатність.
Безвідмовність – властивість об'єкта безупинно зберігати працездатність протягом деякого наробітку або протягом деякого часу. На практиці часто визна-чають імовірність безвідмовної роботи протягом деякого часу.
Довговічність – властивість об'єкта зберігати працездатність до настання граничного стану при встановленій системі технічного обслуговування й ремонтів.
Ремонтопридатність – властивість об'єкта, що полягає в його пристосованості до попередження й виявлення причин виникнення відмов, підтримці й відновленню працездатності шляхом проведення ремонтів і техніч-ного обслуговування. Ремонто–придатність ЕОМ можна оцінити середнім
часом усунення несправності, інакше кажучи, середнім значенням часу відновлення працездатності після відмови.
Наробіток – тривалість або обсяг роботи об’єкта, вимірювана в будь-яких не убутних величинах (одиниця часу, число циклів напруження, кілометри пробігу й т.п.)
Граничний стан – стан об’єкта, при якому його подальша експлуатація повинна бути припинена через непереборне порушення вимог безпеки, або непереборного відходу заданих параметрів за встановлені межі, або непереборного зниження ефективності експлуатації нижче припустимої, або необхідності проведення капітального ремонту.
Працездатність – стан об’єкта, при якому він здатний виконувати задані функції, зберігаючи значення заданих параметрів у межах, установлених нормати-вно-технічною документацією.
Відмова ЕОМ – це таке порушення її працездатності, для усунення якого
потрібні певні дії обслуговуючого персоналу з ремонту, заміні й регулюванню
не справного елемента, вузла або пристрою.
Відмови діляться на раптові й поступові.
Раптова відмова – це, практично, миттєва зміна якого-небудь параметра (наприклад, зростання опору ланцюга внаслідок її обриву, електричний пробій діода й т.п.). Поступова відмова – це нагромадження, що відбувається в часі, кількісних змін деякого параметра, що достигнули значення, при якому машина виявляється в непрацездатному стані.
Безвідмовність ЕМ може бути оцінена середнім часом наробітку машини на одну відмову.
Наслідком відмов характеризуються випадковими величинами тривалості перерви у функціонуванні машини через ремонтні роботи (випадковими величинами тривалості ремонту).
Обчислювальні
системи, компонуються, у загальному
випадку, з не абсолютно надійних ЕМ.
Нехай λ
– інтенсивність потоку відмов у кожній
з N
машин. Отже, величина
 – середній час безвідмовної роботи
однієї ЕМ.
– середній час безвідмовної роботи
однієї ЕМ.
Відновленням називається подія, що полягая в тім, відмовила ЕМ повністю здобуває зданість виконувати задані функції по обробці інформації. Відновлення, що відмовило ЕМ може бути здійснене автоматично (у загальному випадку за допо-могою апаратурно-програмних засобів) або напіватоматично (за участю бригади технічного обслуговування).
Будемо
вважати, що ця процедура реалізується
за допомогою системи, що відновлює, що
складається із m
простроїв,
1 m
m 0.
0.
Після відмови ЕМ або надходить на обслуговування в будь-який вільний пристрій, що відновлює (ВП), або ставиться в чергу на відновлення. Уважається, що в кожний момент часу кожне з m ВП може бути або вільним, або зайнятим відновленням не більше однієї ЕМ.
Нехай μ – інтенсивність відновлення, що відмовили ЕМ одним ВП.
Функція надійності.
Розрахуємо функцію r(t) надійності однієї ЕМ, вираженої в імовірності безвідмовної роботи однієї ЕМ:
 , (5.1)
, (5.1)
Середній час безвідмовної роботи однієї ЕМ:
 ,
(5.2)
,
(5.2)
Згідно
з варіантом,
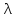 =0,0026
=0,0026 .
.
Розрахуємо середній час без відмовної роботи однієї ЕМ:

Для
розрахунку формули (5.1), треба розрахувати
 :
:
 (5.3)
(5.3)
Розрахуємо функцію надійності для ЕОМ в різних значеннях t, і занесемо дані до таблиці (5.1).
 1
1
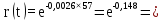 0,86
0,86
 0,74
0,74
 0,64
0,64
 0,55
0,55
 0,48
0,48
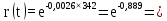 0,41
0,41
 0,35
0,35
 0,31
0,31
 0,26
0,26
 0,23
0,23
 0,2
0,2
 0,17
0,17
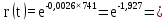 0,16
0,16
 0,13
0,13
 0,11
0,11
 0,09
0,09
 0,08
0,08
 0,07
0,07
 0,06
0,06
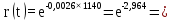 0,05
0,05
Таким чином, результати розрахунку функції надійності наведені у таблиці (5.1).
Таблиця
5.1 – Значення
функції надійності ЕОМ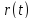 і аргументуt
і аргументуt
|
t |
0 |
57 |
114 |
171 |
228 |
285 |
342 |
399 |
456 |
513 |
570 |
|
r(t) |
1 |
0,86 |
0,74 |
0,64 |
0,55 |
0,48 |
0,41 |
0,35 |
0,31 |
0,26 |
0,23 |
|
t |
625 |
684 |
741 |
798 |
855 |
912 |
969 |
1026 |
1083 |
1140 |
– |
|
r(t) |
0,2 |
0,17 |
0,16 |
0,13 |
0,11 |
0,09 |
0,08 |
0,07 |
0,06 |
0,05 |
– |
Побудуємо графік функції надійності:

Рисунок 5.1 – Графік функції надійності r(t)
Розрахуємо функцію надійності комп’ютерної системи по формулі:
 ,
(5.4)
,
(5.4)
де Λ – інтенсивність потоку відмов комп’ютерної системи.
Λ знаходиться по формулі:
 , (5.5)
, (5.5)
Розрахуємо інтенсивність потоку відмов комп’ютерної системи:
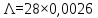 =
0,0988
(
=
0,0988
( ),
),
Середній час безвідмовної роботи комп’ютерної системи знаходиться по формулі:
 , (5.6)
, (5.6)
Для
того,
щоб розрахувати
R(t),
треба розрахувати
 :
:
 ,
(5.7)
,
(5.7)
Розрахуємо функцію надійності КС в різних значеннях t, і занесем дані до таблиці (5.2).
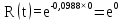 =1
=1
 0,9
0,9
 0,82
0,82
 0,74
0,74
 0,67
0,67
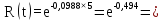 0,61
0,61
 0,55
0,55
 0,5
0,5
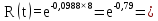 0,45
0,45
 0,41
0,41
 0,37
0,37
 0,34
0,34
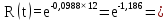 0,31
0,31
 0,28
0,28
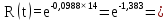 0,25
0,25
 0,23
0,23
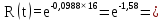 0,21
0,21
 0,19
0,19
 0,17
0,17
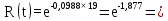 0,15
0,15
 0,14
0,14
Таким чином, результати розрахунку функції надійності наведені у таблиці (5.2).
Таблиця
5.2 – Значення
функції надійності КС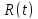 і аргументуt
і аргументуt
|
t |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
R(t) |
1 |
0,9 |
0,82 |
0,74 |
0,67 |
0,61 |
0,55 |
0,5 |
0,45 |
0,41 |
0,37 |
|
t |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
– |
|
R(t) |
0,34 |
0,31 |
0,28 |
0,25 |
0,23 |
0,21 |
0,19 |
0,17 |
0,15 |
0,14 |
– |
Графік функції надійності побудован в додатку Г.
Функція відновлення показує ймовірність того, що комп'ютер буде віднов-лений в певний момент часу, і є показником ремонтопридатності.
Функція відновлення ЕОМ визначається по формулі:
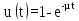 ,
(5.8)
,
(5.8)
де µ – інтенсивність відновлення, t – час відновлення.
Згідно
з моїм варіантом,
µ=0,75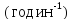 .
.
Знайдемо
 за формулою:
за формулою:
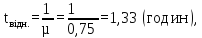 (5.9)
(5.9)
Розрахуємо параметри функції відновлення:
 .
(5.10)
.
(5.10)
Розрахуємо функцію відновлення ЕОМ в різних значеннях t, і занесем дані до таблиці (5.3).
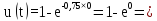 0
0
 1-0,86=
0,14
1-0,86=
0,14
 1-0,74=0,26
1-0,74=0,26
 1-0,63=0,37
1-0,63=0,37
 1-0,55=0,45
1-0,55=0,45
 1-0,47=0,53
1-0,47=0,53
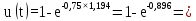 1-0,41=0,59
1-0,41=0,59
 1-0,35=0,65
1-0,35=0,65
 1-0,3=0,7
1-0,3=0,7
 1-0,26=0,74
1-0,26=0,74
 1-0,22=0,78
1-0,22=0,78
 1-0,19=0,81
1-0,19=0,81
 1-0,17=0,83
1-0,17=0,83
 1-0,14=0,86
1-0,14=0,86
 1-0,12=0,88
1-0,12=0,88
 1-0,11=0,89
1-0,11=0,89
 1-0,09=0,91
1-0,09=0,91
 1-0,08=0,92
1-0,08=0,92
 1-0,07=0,93
1-0,07=0,93
 1-0,06=0,94
1-0,06=0,94
 -0,05=0,95
-0,05=0,95
Таким чином, результати розрахунку функції надійності наведені у таблиці (5.3).
Таблиця 5.3 – Точки функції відновлення ЕОМ
|
t |
0 |
0,199 |
0,398 |
0,597 |
0,796 |
0,995 |
1,194 |
1,393 |
1,592 |
1,791 |
1,99 |
|
u(t) |
0 |
0,14 |
0,26 |
0,37 |
0,45 |
0,53 |
0,59 |
0,65 |
0,7 |
0,74 |
0,78 |
Продовження таблиці 5.3
|
t |
2,189 |
2,388 |
2,587 |
2,786 |
2,985 |
3,184 |
3,383 |
3,582 |
3,781 |
3,98 |
|
u(t) |
0,81 |
0,83 |
0,86 |
0,88 |
0,89 |
0,91 |
0,92 |
0,93 |
0,94 |
0,95 |
Графік функції відновлення ЕОМ зображений на рисунку 5.2

Рисунок 5.2 – Графік функції відновлення однієї ЕОМ
Розрахуємо функцію відновлення КС.
Функція відновлення КС визначається по формулі:
 , (5.11)
, (5.11)
де m – кількість пристроїв, що відновлюють (у тому числі віртуальних).
Згідно з моїм варіантом, m = 4.
Розрахуємо
 по формулі:
по формулі:
 , (5.12)
, (5.12)
Розрахуємо функцію відновлення КС в різних значеннях t, і занесем дані до таблиці (5.4):
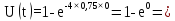 0
0
 0,14
0,14
 0,26
0,26
 0,36
0,36
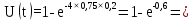 0,45
0,45
 0,53
0,53
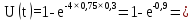 0,59
0,59
 0,65
0,65
 0,7
0,7
 0,74
0,74
 0,78
0,78
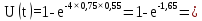 0,81
0,81
 0,83
0,83
 0,86
0,86
 0,88
0,88
 0,89
0,89
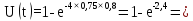 0,91
0,91
 0,92
0,92
 0,93
0,93
 0,94
0,94
 0,95
0,95
Таким чином, результати розрахунку функції надійності наведені у таблиці (5.4).
Таблиця 5.4 – Точки функції відновлення КС
|
t |
0 |
0,05 |
0,1 |
0,15 |
0,2 |
0,25 |
0,3 |
0,35 |
0,4 |
0,45 |
0,5 |
|
U(t) |
0 |
0,14 |
0,26 |
0,36 |
0,45 |
0,53 |
0,59 |
0,65 |
0,7 |
0,74 |
0,78 |
|
t |
0,55 |
0,6 |
0,65 |
0,7 |
0,75 |
0,8 |
0,85 |
0,9 |
0,95 |
1 |
– |
|
U(t) |
0,81 |
0,83 |
0,86 |
0,88 |
0,89 |
0,91 |
0,92 |
0,93 |
0,94 |
0,95 |
– |
Графік функції відновлення КС зображений на рисунку 5.3

Рисунок 5.3 – Графік функції відновлення КС
Коефіцієнт готовності – це ймовірність того, що обчислювач, або комп'ютерна система готови до вирішення задач у любий момент часу.
Розрахуємо коефіцієнт готовності ЕОМ.
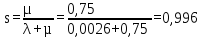 . (5.12)
. (5.12)
Розрахуємо коефіцієнт готовности КС.
 . (5.13)
. (5.13)
Продуктивність КС
Щоб розрахувати максимальну продуктивність КС, треба скористатися формулою:
 , (5.14)
, (5.14)
де
 – продуктивність одного компьютера
згідно з моїм варіантом,
– продуктивність одного компьютера
згідно з моїм варіантом,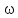 = 3,4 (ГФлопс).
= 3,4 (ГФлопс).
Підставимо дані у формулу, та розрахуємо максимальну продуктивність КС:
 ,
,
Для того, щоб розрахувати середню продуктивність, треба скористатися формулою:
 ),
(5.15)
),
(5.15)
Для оцінки реальної продуктивності КС треба скористатися формулою:
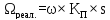 ,
(5.16)
,
(5.16)
де
 – коефіцієнт прискорення, який дорівнює
– коефіцієнт прискорення, який дорівнює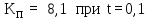 .
.
Зробимо підстановку у нашу формулу, и розрахуємо: