Вариационный ряд. Гистограмма

Модой называют варианту, которая имеет наибольшую частоту.

Медианой называют варианту, которая делит вариационный ряд на две части, равные по числу вариант. Если число вариант нечетно, т. е. , то ; при четном медиана

Гистограммой частот называют ступенчатую фигуру, состоящую из прямоугольников, основаниями которых служат частичные интервалы длиною h, а высоты равны отношению (плотность частоты).

Для построения гистограммы частот на оси абсцисс откладывают частичные интервалы, а над ними проводят отрезки, параллельные оси абсцисс на расстоянии . Площадь i-го участка гистограммы равна — Сумме частот вариант i-го интервала. Площадь гистограммы частот равна объему выборки.

Гистограммой относительных частот называют ступенчатую фигуру, состоящую из прямоугольников, основаниями которых служат частичные интервалы длиною h, а высоты равны отношению — (плотность относительной частоты)

Площадь i-го участка гистограммы равна —относительной частоте вариант i-го интервала. Площадь гистограммы частот равна сумме относительных частот вариант, т.е. единице.

Точечное оценивание параметров распределения. Требования к оценкам:несмещенность, эффективность.

Точечной называют оценку, которая определяется одним числом.

Пусть есть статистическая оценка неизвестного параметра теоретического распределения. Допустим, что по выборке объема n найдена оценка . Повторим опыт, т. е. извлечем из генеральной совокупности другую выборку того же объема и по ее данным найдем оценку . Повторяя опыт многократно, получим числа , которые, вообще говоря, будут различны между собой. Таким образом, оценку можно рассматривать как случайную величину, а числа — как ее возможные значения.

Представим себе, что оценка дает приближенное значение с избытком; тогда каждое, найденное по данным выборок, число будет больше истинного значения . Ясно, что в этом случае и математическое ожидание (среднее значение) случайной величины будет больше, чем , т. е. . Очевидно, что если дает оценку с недостатком, то .

Соблюдение требований гарантирует от получения систематических ошибок.

Несмещенной называют статистическую ошибку , математическое ожидание которой равно оцениваемому параметру при любом объеме выборки, т. е

Смещенной называют оценку, математическое ожидание которой не равно оцениваемому параметру.

Эффективной называют статистическую оценку, которая (при заданном объеме выборки n) имеет наименьшую возможную дисперсию.

Выборочная средняя и выборочная дисперсия.

Выборочная средняя

Пусть для изучения генеральной совокупности относительно количественного признака X извлечена выборка объема n.

Выборочной средней называют среднее арифметическое значение признака выборочной совокупности Если все значения х₁,х₂… признака выборки объема n различны то х^-_в=(х₁+…х_n)/n

Если все значения х₁,х₂… имеют соответственно частоты n₁,n₂…, причем n₁+n₂+…n_k=n, то х^-_в=(х₁n₁+…+х_kn_k)/n или

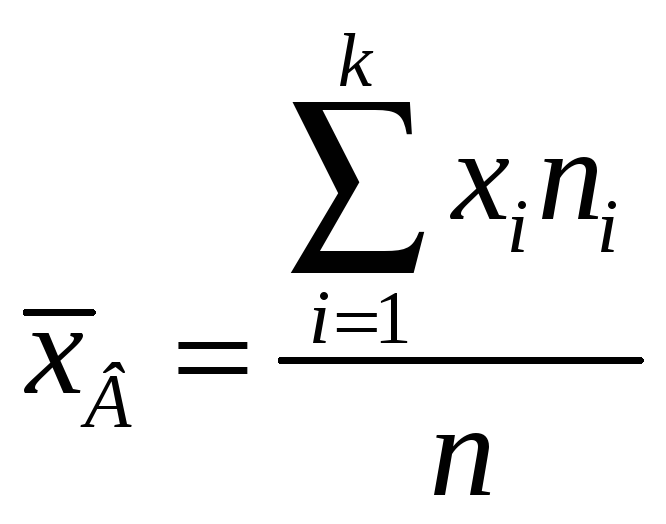
Выборочной дисперсией называют среднее арифметическое квадратов отклонений значений признака генеральной совокупности от их среднего значения .