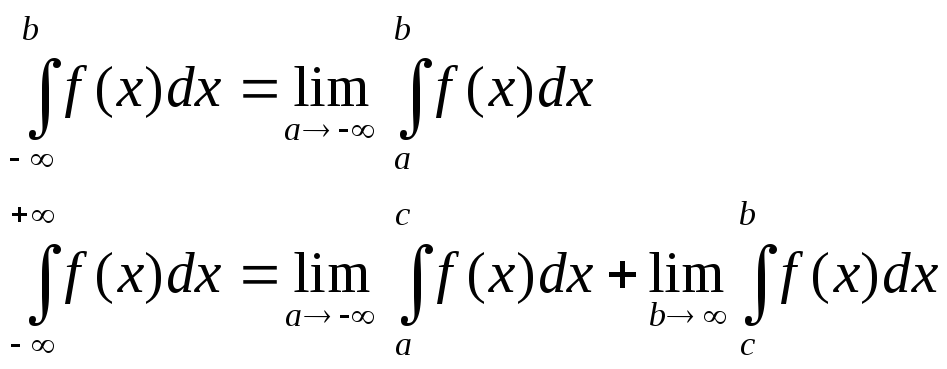- •1 Понятие функции.
- •2 Предел последовательности.
- •3 Бесконечнобольшие(б.Б.) и бесконечномалые(б.М.) последовательности.
- •4. Предел функции.
- •5 Бесконечно большие(б.Б.) и бесконечно малые(б.М.) функции.
- •6 Основные теоремы о пределах.
- •8 Первый замечательный предел.
- •7. Сравнение бесконечно малых величин.
- •9. Непрерывность функций
- •10 Свойства функций, непрерывных в точке
- •11. Дифференцирование
- •13 Дифференцируемость функции
- •14 Правила дифференцирования.
- •15 Производные элементарных функций
- •16 Производная сложной функции
- •17 Производная обратной функции
- •18 Понятие дифференциала
- •19 Производная и дифференциал высших порядков
- •24 Правило Лапиталя
- •25 Монотонность функций.
- •26 Экстремумы функций.
- •28, 29 Направление выпуклостей и точки перегиба графика функций.
- •30 Асимптоты графика функций
- •31 Схема исследования функции и исследование её графика
- •32 Формула Тейлора
- •33.Функция нескольких переменных.
- •34 Предел функции двух переменных.
- •36, 37 Частные производные
- •38Понятие дифференцируемости
- •40 Производные сложных функций
- •41 Дифференциал функции
- •42 Производная по направлению и градиент
- •43 Экстремум функции двух переменных
- •44 Условный экстремум
- •45 Минимум и максимум функции двух переменных
- •46 Неопределённый интеграл
- •47 Таблица основных интегралов
- •49 Метод подстановки
- •50 Метод интегрирования по частям
- •51 Определённый интеграл (определение, геометрический смысл)
- •55 Формула Ньютона-Лейбница.
- •52 Основные свойства определённого интеграла
- •54 Интеграл с переменным верхним пределом
- •56 Не собственный Интеграл с бесконечными пределами интегрирования
52 Основные свойства определённого интеграла
1)
![]() ;
2)
;
2)
![]() ;
3)
;
3)
![]() ;
;
4)
![]() ;
;
5)
![]() .
.
53
Теорема о среднем:
если функция y=f(x)
непрерывна на отрезке [a;b],
то
![]() .
Док-во:
.
Док-во:
![]() =по
формуле Ньютона-Лейбница, разложим по
формуле Лагранжа= F’(c)(b-a)=f(c)(b-a).
=по
формуле Ньютона-Лейбница, разложим по
формуле Лагранжа= F’(c)(b-a)=f(c)(b-a).
54 Интеграл с переменным верхним пределом
Рассмотрим
интеграл
![]() .
В данном интеграле нижний предел=const,
а верхний предел – переменная. Величина
этого интеграла является функцией
зависящей от верхнего предела х, обозначим
её как Ф(х) и этот интеграл назовём
Интегралом с переменным верхним пределом.
.
В данном интеграле нижний предел=const,
а верхний предел – переменная. Величина
этого интеграла является функцией
зависящей от верхнего предела х, обозначим
её как Ф(х) и этот интеграл назовём
Интегралом с переменным верхним пределом.
Теорема
Барроу: Производная от непрерывной
функции по переменному верхнему пределу
существует и равна подынтегральной
функции в точке, равной верхнему пределу,
т.е.
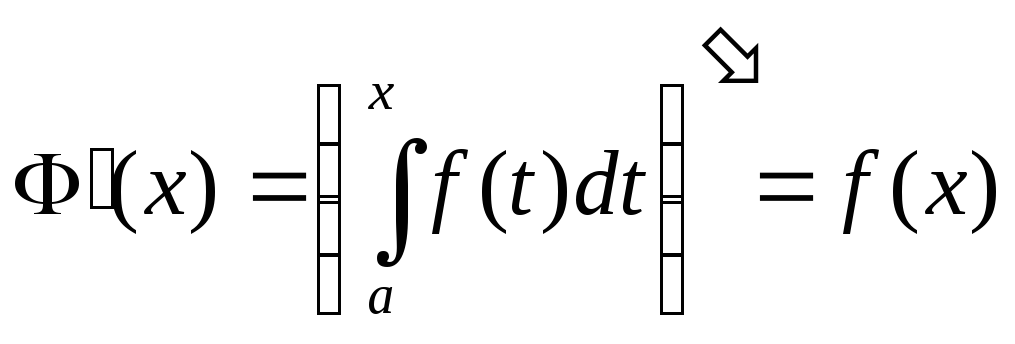 .
.
56 Не собственный Интеграл с бесконечными пределами интегрирования
Определение:
пусть функция y=f(x)
определена на промежутке [a;)
интегрируема по любому промежутку
внутри этого интервала, т.е. существует
![]() .
Тогда если существует предел
.
Тогда если существует предел
![]() ,
то он называется несобственным интегралом
первого рода.
,
то он называется несобственным интегралом
первого рода.
Замечание: если предел существует и конечен, то несобственный интеграл – сходящийся, если предел не существует или равен бесконечности, то интеграл – расходящийся.