§10. Основные понятия об n-мерном арифметическом пространстве

1. Определение. n-мерным арифметическим пространством называется множество всех строк (или столбцов), состоящих из n действительных чисел.

Строка называетсяточкой в , а числа еекоординатами в стандартной системе координат. Точка называетсяначалом координат, а множество точек вида --ойкоординатной осью (обозначается ). Здесь. Расстоянием от точки до точкив (или, что тоже самое, длиной отрезка ) называется число

.

Вектором в с началом в точке и концом в точкеназывается строка (или столбец), составленная из разностей координат точеки:

.

Над векторами в определяются операции сложения и умножения на числа по соответствующим правилам, определенным в §2 для матриц.

Единичные векторы, направленные вдоль координатных осей, т. е. векторы ,,…, называютсястандартным базисом в , числа -координатами вектора в стандартном базисе. При этом очевидно равенство.

2. Скалярным произведением векторов ив называется число .

Модулем вектора называется число

.

Векторы иназываютсяперпендикулярными, если их скалярное произведение равно нулю: .

Теорема (Неравенство Буняковского). Для любых векторов ииз справедливо неравенство .

Углом между векторами ив называется такой угол , что

.

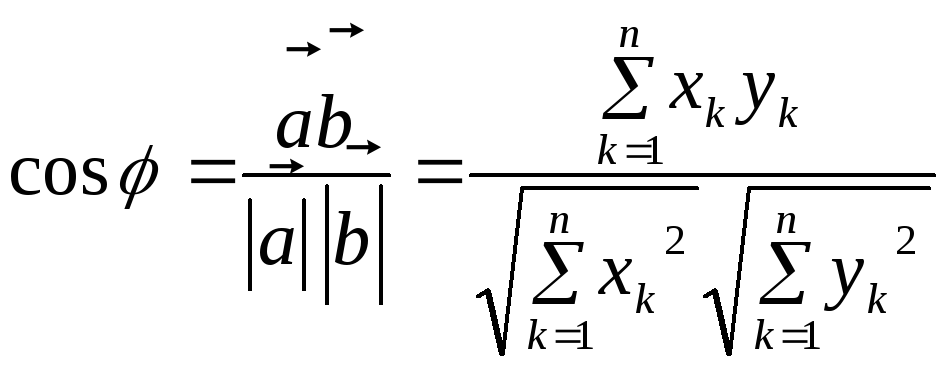3. Гиперплоскостью в называется множество всех его точек, координаты которых удовлетворяют уравнению

.

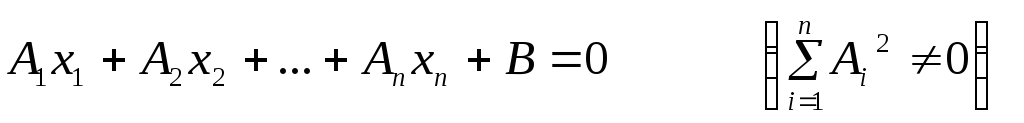Глава 3. Введение в анализ.

§1. Функции

1.1. Функция. Способы задания функций

Пусть DиЕ -некоторые множества.

Определение.Функцией собластью определения и областью значений называется некоторое отображение изв, т. е. соответствие, при котором каждому элементусопоставляется единственный элемент.

Если DиЕ -некоторые множества чисел, то функцияназываетсячисловой. В этом случае говорят также, что задананезависимая переменная (аргумент)х,которая может принимать значения из множестваD,и каждомухDприведено в соответствие определённое значение (число) другой переменнойуЕ,называемой функцией илизависимой переменной. Числовые функции можно задавать следующими способами.

а) Табличный.

б) Графический. Графиком функцииу=f(x) называется множество точек (х,у) плоскоститаких, что и.

в) Аналитический.Аналитическим способом, т.е. с помощью одной формулы, можно задавать только элементарные функции.

1.2. Элементарные функции

Функции C(постоянная); (степенная); (показательная, а>0, ); (логарифмическая, а>0, );sinx, cosx, tgx, ctgx (тригонометрические); arcsinx, arccosx, arctgx, arcctgx (обратные тригонометрические) называютсяосновными элементарными функциями.

Применяя к этим функциям арифметические действия и операции функции от функции (суперпозиции) в конечном числе, можно получать новые функции, которые называются элементарнымифункциями.Областью определения элементарной функцииназывается множество всех значений аргументахпри которых выражениеимеет смысл.

§2. Теория пределов

2.1. Последовательность и её предел

Числовой последовательностью называется действительная функция натурального аргумента, т. е. функция у которой.

Определение. Число а называется пределом последовательности (), если для любого числа найдётся число, что все числа, у которыхудовлетворяют неравенству.