
- •Глава I. Линейная алгебра
- •§1. Матрицы. Определители 1-го, 2-го, 3-го порядков. Свойства определителей
- •§2. Миноры и алгебраические дополнения. Разложение определителя по элементам строки или столбца
- •§3. Операции над матрицами
- •§4. Системы линейных алгебраических уравнений (слау). Матричный метод решения
- •§5. Метод Гаусса для исследования и решения слау
- •§6. Однородные системы линейных алгебраических уравнений
- •Глава 2. Элементы векторной алгебры и аналитической геометрии
- •§1. Векторы и линейные операции над ними
- •§2. Базис векторного пространства. Координаты вектора
- •Теорема. При сложении векторов их соответствующие координаты складываются, при умножении вектора на число все его координаты умножаются на это число.
- •§3. Скалярное произведение векторов и его свойства
- •§4. Векторное произведение векторов и его свойства
- •§5. Смешанное произведение векторов
- •§6. Прямая на плоскости
- •§7. Плоскость в пространстве
- •§8. Прямая в пространстве
- •§9. Кривые второго порядка на плоскости
- •§10. Основные понятия об n-мерном арифметическом пространстве
- •Глава 3. Введение в анализ.
- •§1. Функции
- •1.1. Функция. Способы задания функций
- •1.2. Элементарные функции
- •§2. Теория пределов
- •2.1. Последовательность и её предел
- •2.2. Предел функции
- •§3. Бесконечно малые и бесконечно большие функции
- •3.5. Сравнение бесконечно малых
- •§4. Непрерывность функций. Точки разрыва
- •4.1. Непрерывность функции в точке
- •4.2. Классификация точек разрыва
- •Глава 4. Дифференциальное исчисление фуннкций одной переменной
- •§1. Приращения и производные
- •§2. Механический и геометрический смыслы производной
- •§3. Правила дифференцирования
- •§4. Дифференциал функции
- •§5. Производные и дифференциалы высших порядков
- •§6. Правило Лопиталя. Раскрытие неопределенностей
- •§7. Исследование функций с помощью производных
- •7.1. Монотонность и экстремумы функции
- •7.2. Выпуклость и точки перегиба функции
- •7.3. Асимптоты графика функции.
- •7.4. Схема исследования и построения графика функции
- •6. Построение таблицы, в которой указываются все найденные точки разрыва, критические точки первого и второго порядка и интервалы между ними. В каждом интервале характеризуется поведение функции.
- •Глава 5. Функции нескольких переменных
- •§1. Основные понятия о функциях нескольких переменных
- •1.2. Способы задания функции нескольких переменных
- •§2. Дифференцирование функций нескольких переменных
- •2.1. Частные приращения и частные производные
- •2.2. Полное приращение и полный дифференциал
- •§3. Производные и дифференциалы высших порядков
- •§4. Экстремумы функции нескольких переменных
- •Глава 6. Неопределенные и определенные интегралы
- •§1. Первообразная и неопределенный интеграл. Их свойства
- •1.1. Основные определения
- •1.2. Таблица основных неопределенных интегралов
- •§3. Определенный интеграл как предел интегральных сумм
- •§4. Свойства определенного интеграла
- •§5. Несобственные интегралы
- •Глава 7. Обыкновенные дифференциальные уравнения
- •§1. Основные понятия об уравнениях первого порядка
- •§2. Уравнения с разделяющимися переменными
- •§3. Однородные уравнения первого порядка
- •§4. Линейные уравнения первого порядка
- •§5. Основные понятия об уравнениях высшего порядка
- •§6. Линейные дифференциальные уравнения (лду)
- •6.1. Линейные дифференциальные уравнения n-го порядка
- •6.2. Однородные линейные дифференциальные уравнения (олду)
- •6.3. Линейная независимость функций
- •6.4. Общее решение линейного однородного дифференциального уравнения n-го порядка
- •6.5. Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами
- •6.6. Общее решение линейного неоднородного дифференциального уравнения
- •6.7. Линейные дифференциальные уравнения второго порядка с постоянными коэффициентами и специального вида правой частью.
- •Содержание
§3. Скалярное произведение векторов и его свойства
Определение.
Скалярным
произведением векторов
![]() и
и![]() называется число, равное произведению
модулей этих векторов на косинус угла
между ними, т. е.
называется число, равное произведению
модулей этих векторов на косинус угла
между ними, т. е.
![]() .
.
Для любых векторов справедливы следующие свойства.
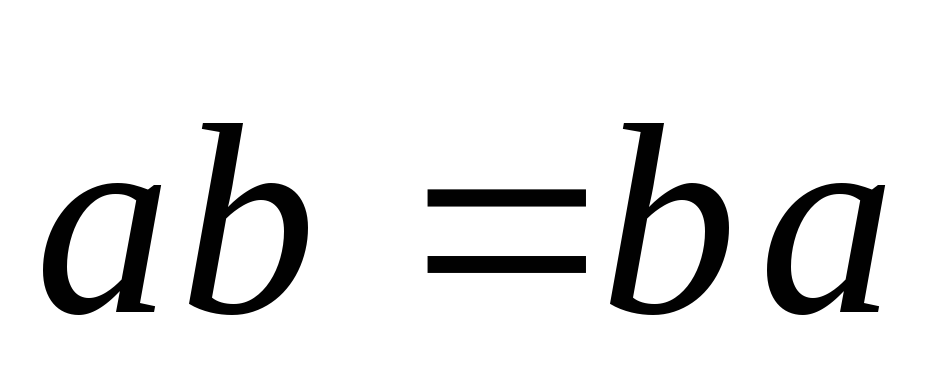 .
.
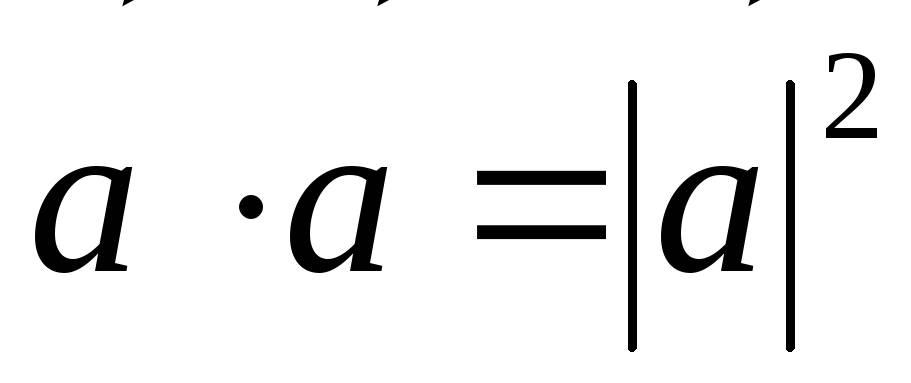 ,
т. к.
,
т. к.
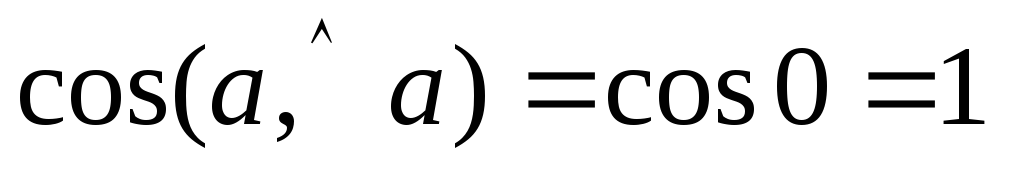 .
.
3) Скалярное
произведение ненулевых векторов
![]() и
и![]() равно
равно![]() только в том случае, когда эти векторы
ортогональны (перпендикулярны).
только в том случае, когда эти векторы
ортогональны (перпендикулярны).
Проекцией
вектора
![]() на
ненулевой вектор
на
ненулевой вектор
![]() (обозначение
(обозначение![]() )
называется его проекция на осьl,
проведенную через вектор
)
называется его проекция на осьl,
проведенную через вектор
![]() (см. рис. 5).
(см. рис. 5).
4 )
)![]() .
.
5) Для
любого вектора
![]() с координатами
с координатами![]() в базисе
в базисе![]() верно:
верно:
![]() ,
,
![]() ,
,![]() .
.
6)
![]() ;
λ –любое
число.
;
λ –любое
число.
7)
![]() .
.
Теорема.
Пусть в
базисе
![]() вектор
вектор![]() имеет координаты
имеет координаты![]() ,
а вектор
,
а вектор![]() –
–![]() .
Тогда
.
Тогда
![]() .
.
Следствие 1.
Модуль
вектора
![]() равен
равен![]() .
.
Следствие 2.
Косинус угла
![]() между векторами
между векторами![]() и
и![]() равен
равен
![]() .
.
Следствие 3.
Ненулевые
векторы
![]() и
и![]() перпендикулярны только в том случае,
когда
перпендикулярны только в том случае,
когда
![]() .
.
§4. Векторное произведение векторов и его свойства
О пределение.
Векторным
произведением
векторов
пределение.
Векторным
произведением
векторов
![]() и
и![]() называется вектор
называется вектор![]()
![]() ,
удовлетворяющий трём условиям:
,
удовлетворяющий трём условиям:
а)
![]()
![]()
в)
![]() перпендикулярен
векторам
перпендикулярен
векторам
![]() и
и![]()
т. е. он перпендикулярен плоскости,
проходящей через векторы
т. е. он перпендикулярен плоскости,
проходящей через векторы
![]() и
и![]() .
.
с)
Тройка
векторов
![]() правая,
т.е. при взгляде со стороны конца третьего
вектора кратчайший поворот от первого
ко второму происходит против часовой
стрелки
(рис. 6).
правая,
т.е. при взгляде со стороны конца третьего
вектора кратчайший поворот от первого
ко второму происходит против часовой
стрелки
(рис. 6).
Для любых векторов справедливы следующие свойства.
1. Векторное произведение антикоммутативно:
![]() .
.
2.
Ненулевые
векторы
![]() коллинеарны только в том случае
когда
коллинеарны только в том случае
когда
![]() .
.
3.
![]() ,
,
![]() - число.
- число.
4.
![]() .
.
Теорема.
Пусть в базисе
![]() векторы
векторы![]() имеют координаты
имеют координаты![]() и
и![]() соответственно. Тогда в этом базисе
соответственно. Тогда в этом базисе
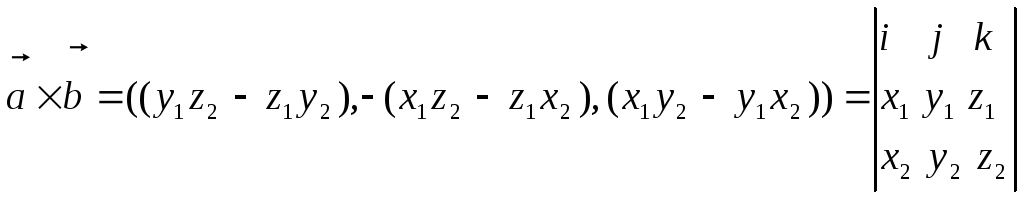 .
.
Следствие
1. Площадь
параллелограмма
построенного на векторах
![]() и
и![]() ,
равна
,
равна
![]() .
.
Площадь треугольника, построенного на этих векторах, равна:
![]() .
.
Следствие
2. Площадь
параллелограмма
построенного на векторах
![]() и
и![]() ,
лежащих в плоскости
,
лежащих в плоскости![]() ,
равна
,
равна
![]() .
.![]()
Площадь треугольника построенного на этих векторах, равна
![]()
§5. Смешанное произведение векторов
Определение.
Смешанным
произведением
трех векторов
![]() называется число, равное скалярному
произведению векторного произведения
векторов
называется число, равное скалярному
произведению векторного произведения
векторов![]() с вектором
с вектором![]() :
(
:
(![]() ).
).
Основные его свойства заключаются в следующей теореме (свойство 1).
1.
Теорема.
Смешанное произведение векторов
![]() равно
равно![]() объему параллелепипеда, построенного
на этих векторах:
объему параллелепипеда, построенного
на этих векторах:
![]()
З десь
знак “+” берется, в случае
если тройка векторов
десь
знак “+” берется, в случае
если тройка векторов
![]()
правая
“”
если она левая (см. рис. 7).
правая
“”
если она левая (см. рис. 7).
2.
Векторы
![]()
являются компланарными только в том
случае
когда их смешанное произведение равно
0:
являются компланарными только в том
случае
когда их смешанное произведение равно
0:
![]()
3.
![]()
![]() .
.
4.
![]() ,.λ
число.
,.λ
число.
5.
![]() .
.
Теорема.
Пусть в базисе
![]() векторы
векторы![]() имеют координаты соответственно
имеют координаты соответственно![]()
![]() и
и![]() ,
тогда их смешанное произведение
записывается в виде определителя:
,
тогда их смешанное произведение
записывается в виде определителя:
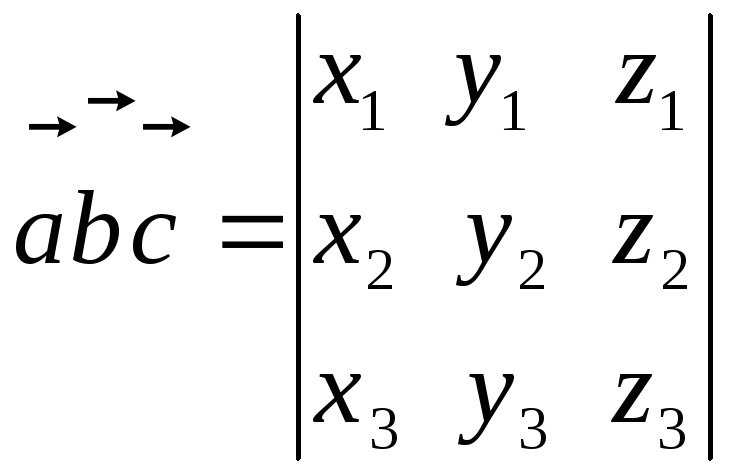 .
.
Следствие.
Объем
параллелепипеда
построенного на векторах
![]()
![]()
![]()
![]() равен:
равен:
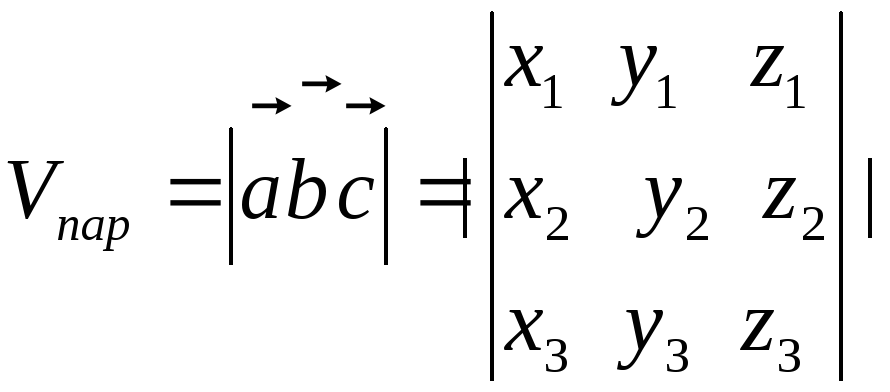 .
.
Объем тетраэдра (треугольной пирамиды), образованного этими векторами равен:
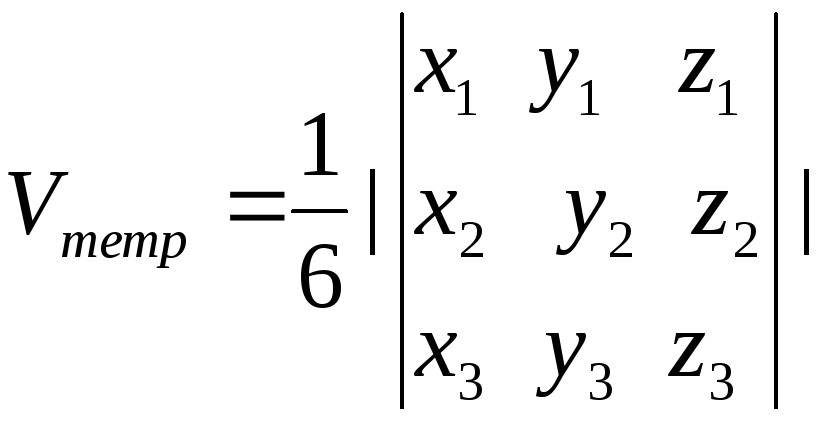 .
.
§6. Прямая на плоскости
1. Уравнение прямой с угловым коэффициентом имеет вид:
![]()
Здесь
![]() - тангенс угла наклона этой прямой к оси
- тангенс угла наклона этой прямой к оси![]() и
и![]() – ордината точки пересечения прямой с
осью
– ордината точки пересечения прямой с
осью![]() (см. рис. 8). С помощью такого уравнения
можно задать любую прямую не перпендикулярную
оси
(см. рис. 8). С помощью такого уравнения
можно задать любую прямую не перпендикулярную
оси![]() .
.
Теорема.
Тангенс
угла
![]() между прямыми
между прямыми![]() и
и![]() определяется формулой
определяется формулой
![]() .
.
Прямые
![]() и
и![]() параллельны
только в том случае когда
параллельны
только в том случае когда
![]() .
.
Прямые
![]() и
и![]() перпендикулярны
только в
том случае, когда
перпендикулярны
только в
том случае, когда
![]() .
.
2.
Общее уравнение прямой:
![]() .
.
Теорема.
Любая
прямая
![]() на плоскости
на плоскости![]() определяется своим общим уравнением и
любое уравнение вида
определяется своим общим уравнением и
любое уравнение вида![]() ,
где
,
где![]() задает некоторую прямую на плоскости.
задает некоторую прямую на плоскости.
Вектор
![]() перпендикулярный прямой
перпендикулярный прямой![]() называетсянормальным
вектором
этой прямой.
называетсянормальным
вектором
этой прямой.
Теорема о
нормальном векторе прямой.
Вектор
![]() с координатами
с координатами![]() является нормальным для прямой
является нормальным для прямой![]() с уравнением
с уравнением![]() на плоскости
на плоскости![]() .
.
Следствие 1.
Косинус
угла
![]() между прямыми
между прямыми![]() и
и![]() с нормальными векторами
с нормальными векторами![]() и
и![]() соответственно, находится по формуле:
соответственно, находится по формуле:
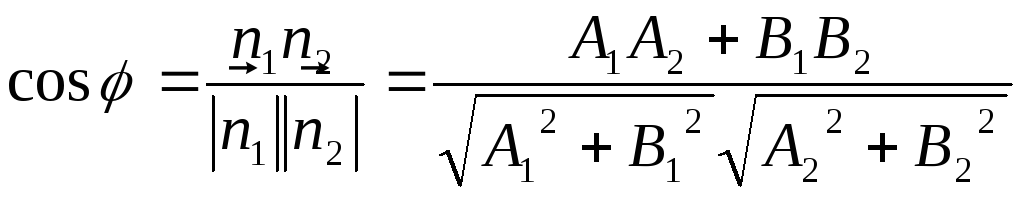 .
.
Следствие 2. Эти прямые перпендикулярны только в том случае, когда
![]() .
.
Следствие 3. Эти прямые параллельны только в том случае, когда
![]() .
.
Если же
![]() ,
то прямые
,
то прямые![]() и
и![]() совпадают
совпадают
