§3. Определенный интеграл как предел интегральных сумм

Криволинейной трапецией называется область на плоскости ограниченная осью, прямыми,гдеи графиком непрерывной на отрезкефункции(см. рис.1).

Р

Рис.1

азбиением отрезка наn частей называется набор чисел из этого отрезка, гдеи. В каждом отрезке (элементарном участке)разбиения выберем некоторую точку. Такое разбиение обозначим буквой, а длину элементарного участка - через. Пусть на отрезкеопределена некоторая функция.

Определение. Интегральной суммой для функции , построенной по разбиениюотрезка, называется сумма произведений значений функции в выбранных точкахна длины элементарных участков.

Обозначение: . Еслив , то приближенно равнаплощади соответствующей криволинейной трапеции.

Определение. Определенным интегралом от функции на отрезкеназывается предел интегральных сумм этой функции по разбиениям отрезка, у которых максимальныйстремится к нулю, т.е.

.

Если в, то этот интеграл выражаетточную площадь соответствующей криволинейной трапеции.

Теорема. Если функция непрерывна на отрезкеили имеет на нем конечное число точек разрыва первого рода, то эта функция интегрируема на, т.е.существует.

§4. Свойства определенного интеграла

В дальнейшем будем считать, что все рассматриваемые функции – интегрируемы в соответствующих отрезках.

1) ,- постоянная.

2) Если на, то.

3) Оценка определенного интеграла снизу и сверху. Если на отрезке функцияограничена снизу и сверху числамиm и , т.е. если на ,то .

4) Теорема о среднем. Пусть функция непрерывна на отрезке, тогда на этом отрезке найдется такая точкаc, что

.

Это значение называетсясредним значением функции на .

5) Оценка модуля определенного интеграла. .

6) Свойство линейности.

6) Свойство аддитивности. Если выполняется неравенство , то

.

Если , то интеграломназывается число. Интегралсчитается равным нулю. Свойство аддитивности справедливо (при условии существования интегралов) для чиселрасположенных в любом порядке, т.е. требованиездесь не обязательно.

Теорема 1. (Ньютона - Лейбница) Пусть функция непрерывна на отрезкеи функцияесть ее первообразная на этом отрезке, тогда

.

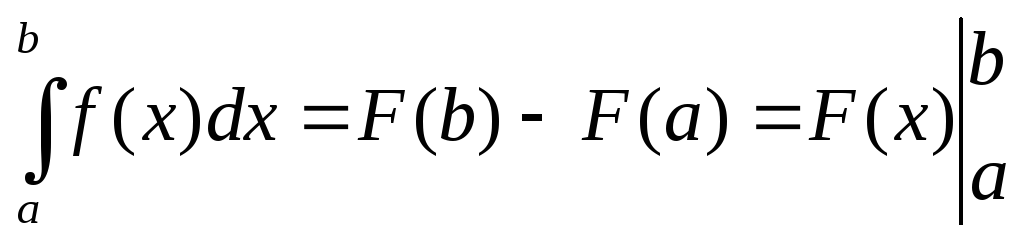Теорема 2. (Замена переменной в определенном интеграле) Пусть функция непрерывна в отрезке, а функциямонотонная и непрерывно дифференцируема в отрезке, где,, тогда

.

Теорема 3. (Нахождение определенного интеграла по частям) Пусть функции инепрерывно дифференцируемы в отрезке, тогда верно равенство

.

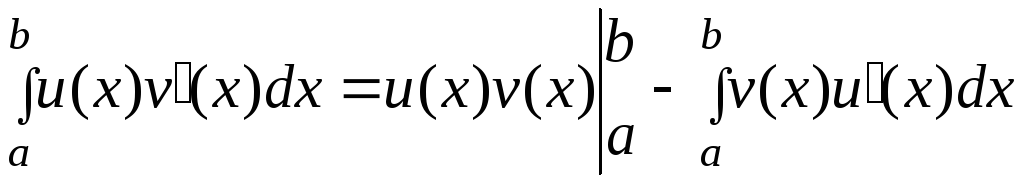Сокращенная запись: .

§5. Несобственные интегралы

5.1. Пусть функция непрерывна в промежутке .Несобственным интегралом от a до от этой функции называется предел:

.

Если этот предел существует (равен числу), то несобственный интеграл называется сходящимся; если он не существует, то интеграл называется расходящимся. В случае, если в промежутке, такой интеграл выражает площадь неограниченной фигуры с границами:,и графиком функции. Для сходящегося интеграла эта площадь конечна, для расходящегося – бесконечна. Формула Ньютона-Лейбница для таких несобственных интегралов имеет вид:

.

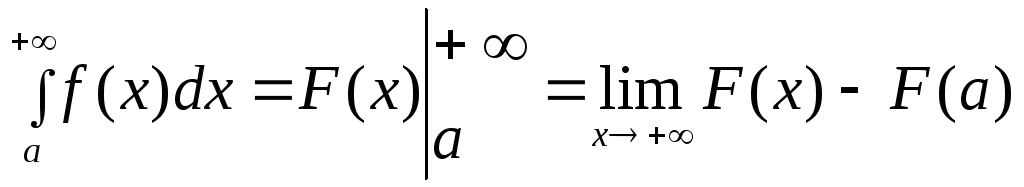5.2. Пусть теперь функция непрерывна в промежутке. Тогданесобственным интегралом от доb называется предел

.

Такой интеграл (при ) выражает площадь фигуры с границами:

, и.

Формула Ньютона-Лейбница: .

5.3. Если функция непрерывна на всей числовой оси, то несобственным интегралом от до называется следующая сумма двух интегралов

(здесь - некоторое число). Это определение не зависит от выбора. Такой интеграл называетсясходящимся, если сходятся оба интеграла:

и .

Если хотя бы один из этих интегралов расходится, то интеграл называетсярасходящимся. При интегралвыражает площадь области с границамии.

Формула Ньютона-Лейбница: .