§4. Экстремумы функции нескольких переменных

4.1. Точка называетсяточкой максимума функции , если существует окрестностьтакая, что для всехиз этой окрестности выполняется неравенство

.

Если для всех из окрестностивыполняется неравенство

,

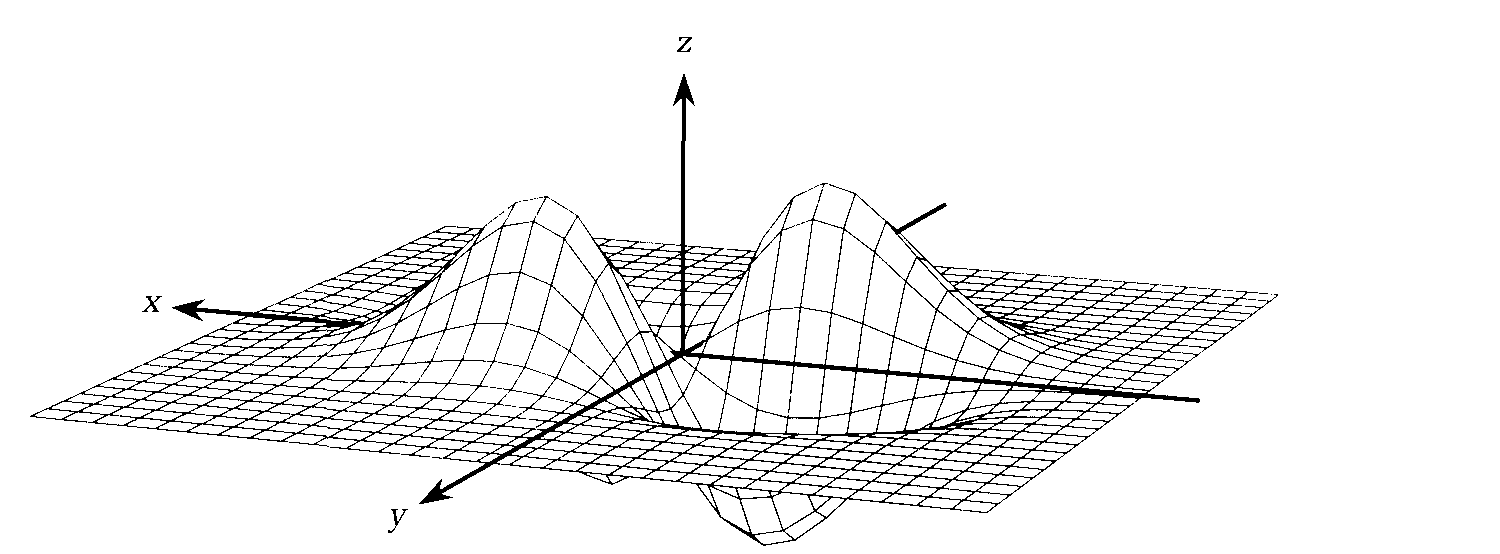
то точка называетсяточкой минимума. Значение функции в точке максимума , называетсямаксимумом функции, а ее значение в точке минимума – минимумом. Точки максимума и минимума называются экстремальными точками функции, а максимумы и минимумы называются экстремумами функции (см. рис. 4).

Рис. 4

Пусть функция определена в некоторой окрестности точки. Если вкаждая частная производнаяиравна нулю или не существует, тоназываетсякритической точкой функции .

Теорема 1. (Необходимое условие экстремума). Если является экстремальной точкой функции, то– критическая точка этой функции.

Сформулируем необходимые условия экстремума для дифференцируемой функции n переменных .

Если точка является экстремальной точкой функции, дифференцируемой в некоторой окрестности, то-стационарная точка этой функции, то есть ее координаты удовлетворяют системе уравнений

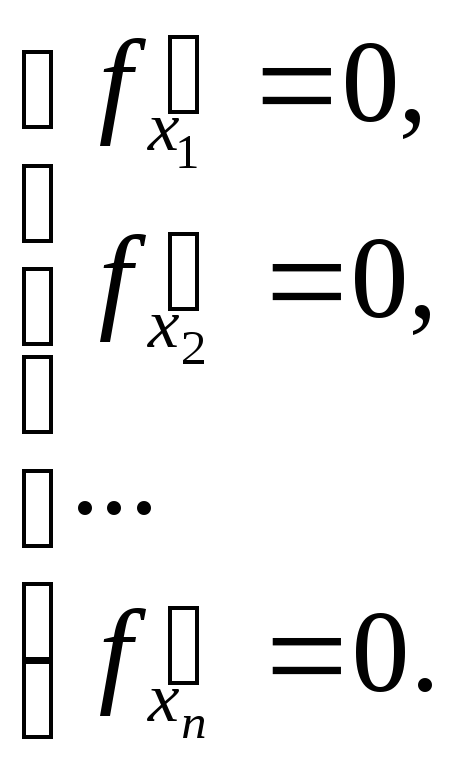
Теорема 2. (Достаточные условия экстремума). Пусть функция трижды дифференцируема в некоторой окрестности своей критической точки. Обозначим,,,. Тогда:

1) Если , то точкаэкстремальная для функции, причем если, то это точка минимума, а если, то точка- точка максимума.

2) Если , то в точкеэкстремума нет.

Глава 6. Неопределенные и определенные интегралы

§1. Первообразная и неопределенный интеграл. Их свойства

1.1. Основные определения

Определение. Первообразной для функции , определенной в интервале, называется такая функция, производная которой совпадает св интервале, т.е.

.

Теорема 1. Если идве первообразные для функциив, то найдется такое числоC, что в.

Из этой теоремы следует, что если есть одна первообразная функции, то любая другая ее первообразная имеет виддля некоторого числа.

Определение. Множество всех первообразных для функции на интерваленазывается еенеопределенным интегралом.

Он обозначается символами , гдезнак интеграла,- дифференциал переменнойx. Если - какая либо первообразная функции, то

, .

1.2. Таблица основных неопределенных интегралов

Здесь u - независимая переменная или непрерывно дифференцируемая функция u=u(x).

1. ,;

2. ;

3. ,. В частности,;

4. ;

5. ;

6. ;

7. ;

8. ;

9. ;

10. ;

11. ;

12. ,;

13. ,;

14. ,;

15. ,;

16. ;

17. ;

18. ;

19. .

1.3. Свойства неопределенных интегралов

Здесь и в дальнейшем предполагается, что все записанные интегралы и производные существуют.

1) ;.

2) ;.

3) Если a- число, то .

4) .

5) Если ;,- числа, то

§2. Основные методы интегрирования

2.1. Метод замены переменной

Теорема 1. Если функция непрерывна, а функциянепрерывно дифференцируема, то

Это равенство можно также записать в виде .

2.2. Метод подведения под знак дифференциала

Следствие. Пусть функции ,,непрерывны, тогда

.

2.3. Метод интегрирования по частям

Теорема 2. Пусть функции инепрерывно дифференцируемы, тогда

.

Последнюю формулу часто записывают в сокращенном виде

.

Этот метод применяется в случае, когда подынтегральная функция имеет вид произведения , где- многочлен, а- тригонометрическая, показательная, обратная тригонометрическая, или логарифмическая функция.

В заключение отметим, что класс функций, первообразные которых находятся в виде элементарных функций (говорят интегрируемых в квадратурах) довольно узок. Например, невозможно записать с помощью элементарной функции.