6. Построение таблицы, в которой указываются все найденные точки разрыва, критические точки первого и второго порядка и интервалы между ними. В каждом интервале характеризуется поведение функции.

7. Построение графика функции с учетом ее асимптот и таблицы. При необходимости можно вычислить промежуточные значения функции.

Глава 5. Функции нескольких переменных

§1. Основные понятия о функциях нескольких переменных

1.1. Пусть имеется переменных величин и каждому набору их значенийиз некоторого подмножествасоответствует определенное значение переменной величины. Тогда говорят, что заданафункция нескольких переменных . Переменные называются независимыми переменными или аргументами, -зависимой переменной, а символ означает закон соответствия. Множествоназываетсяобластью определения функции. Пусть теперь - некоторое подмножество на плоскости(в пространстве).

Определение. Функцией двух (трех) переменных называется функция, область определения которой есть некоторое подмножество плоскостиR² (см. рис. 1) (пространства R³), а область значений принадлежит действительной осиR.

С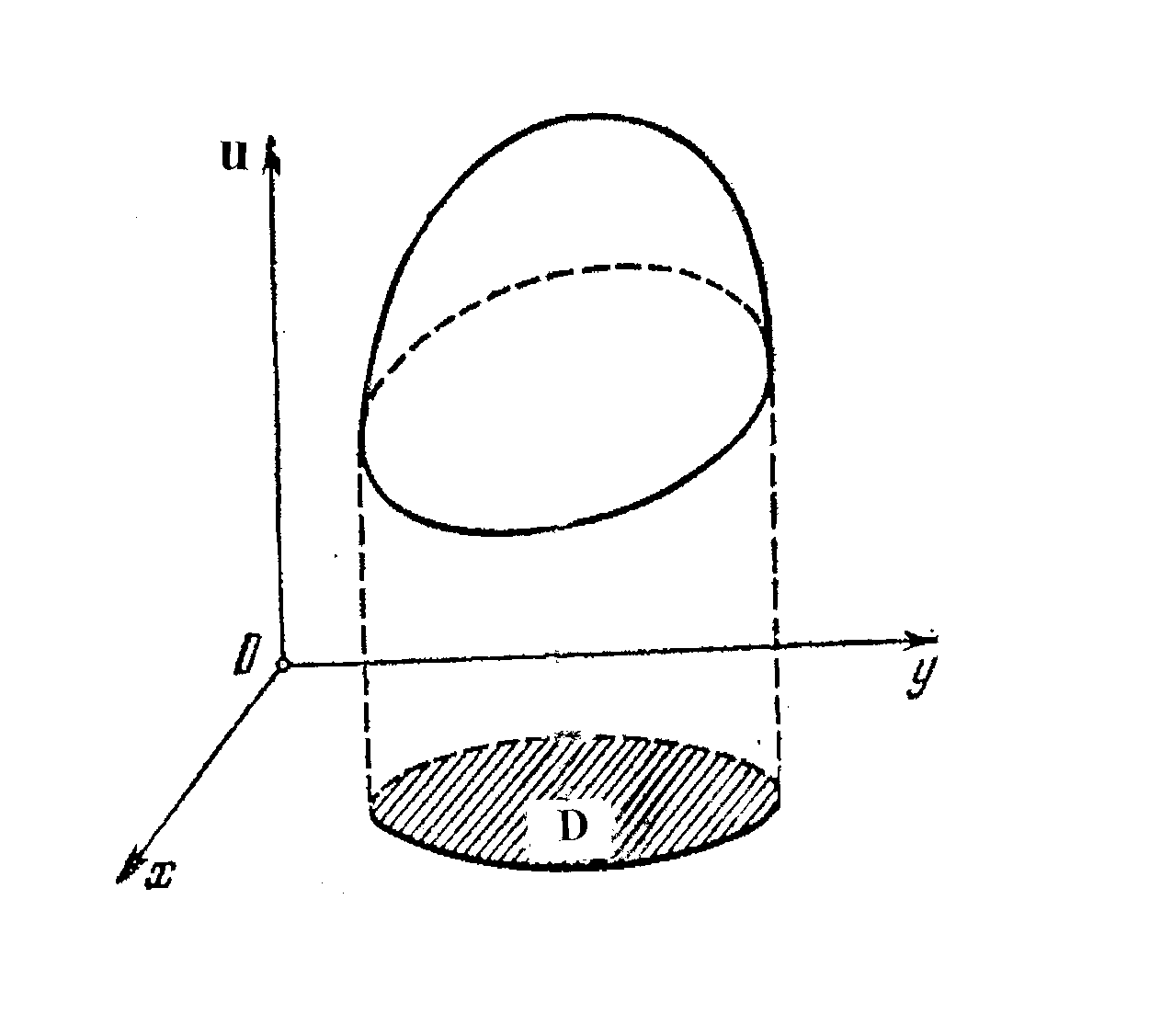оответствующие обозначения: .

Рис. 1

Окрестностью точки на плоскости (илив пространстве) радиусаназывается круг без окружности (или шар без сферы) радиусас центром в точке.

Т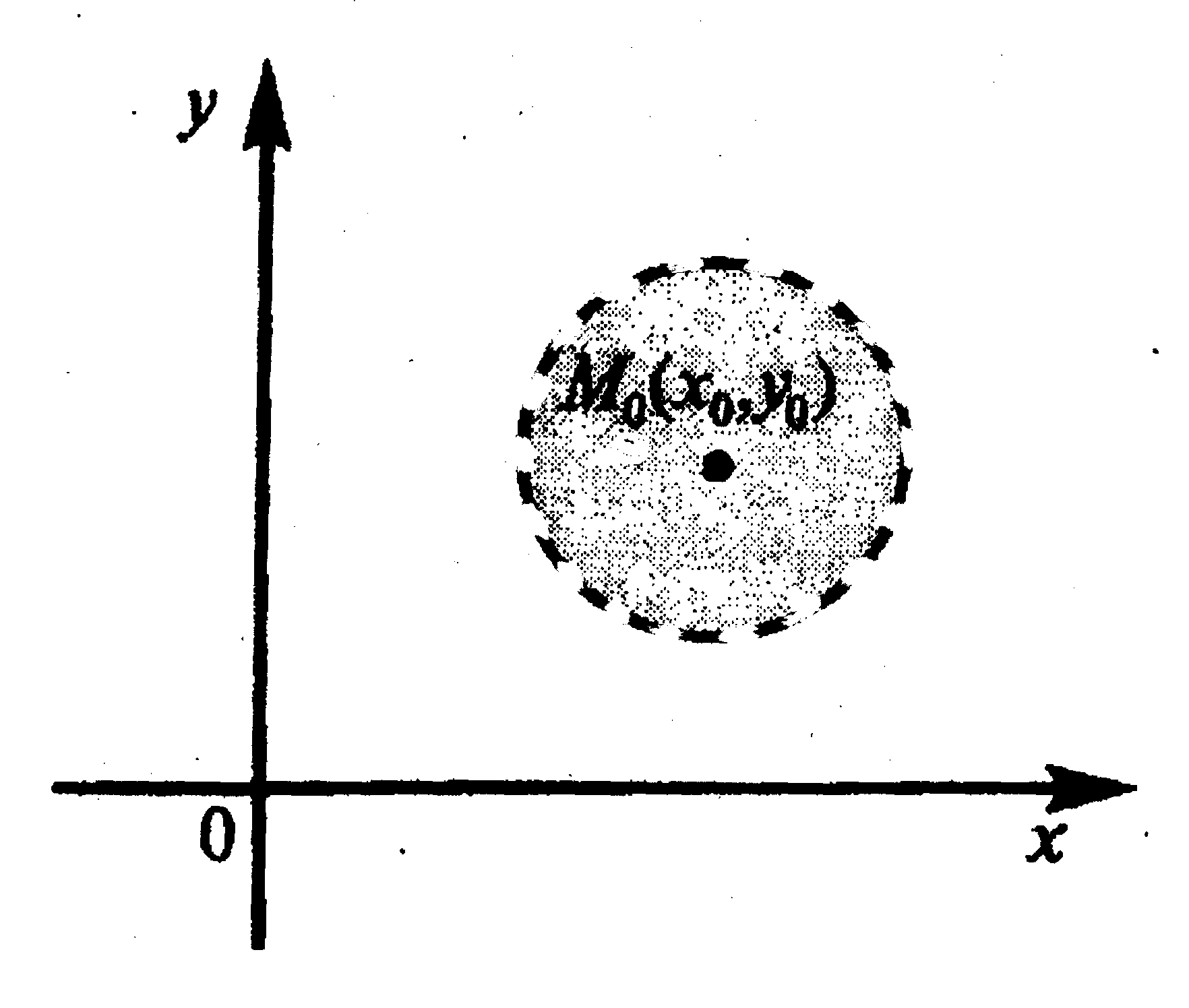акую окрестность будем обозначать через. Здесьn=2 или 3. Если , то(см. рис. 2).

Рис. 2

Точка называетсяграничной точкой для множества , если окрестностилюбого радиусаэтой точки пересекаются как с множеством, так и с его дополнением. Множество всех граничных точек множестваназываетсяграницей этого множества и обозначается через .

Множество , содержащее всю свою границу, называетсязамкнутым. Множество , не содержащее ни одной точки своей границы, называетсяоткрытым.

1.2. Способы задания функции нескольких переменных

а) Табличный способ. Таблица функции двух переменных имеет прямоугольную форму, её строки и столбцы отмечены значениями соответственно первой и второй переменных этой функции. Например, таблица функции z=f(x,y) имеет вид:

x\y	y1	y2	…	yn	…
x1	z11	z12	…	z1n	…
x2	z21	z22	…	z2n	…
…	…	…	…	…	…
xm	zm1	zm2	…	zmn	…
…	…	…	…	…	…

Здесь z_ij=f(x_i,y_j), точки (x_i,y_j) принадлежат области определения функции.

б) Аналитический способ. Этот способ позволяет задать функцию нескольких переменных с помощью одной формулы, включающей в себя переменные, основные элементарные функции, их суперпозиции и четыре арифметических действия. Такие функции называются элементарными.

Аналитически заданная (элементарная) функция имеет естественную область определения – множество всех значений аргументов функции, при которых выражение, определяющее функцию, имеет смысл.

в) Графический способ. Графиком функции двух переменных называется поверхность в пространствеобразованная множеством точек, координаты которых удовлетворяют уравнению. Проекция графика функции на плоскостьсовпадает с областью определенияэтой функции (см. рис.1).

Пусть – число.Линией уровня функции двух переменныхназывается множество всех точекиз ее области определения, координаты которых удовлетворяют уравнению. Например, линии уровня функции, изображенные на рис.3, соответствуют значениям.

Рис. 3

Поверхностью уровня функции трех переменныхназывается множество всех точекиз области определенияфункции, координаты которых удовлетворяют уравнению