
- •Глава I. Линейная алгебра
- •§1. Матрицы. Определители 1-го, 2-го, 3-го порядков. Свойства определителей
- •§2. Миноры и алгебраические дополнения. Разложение определителя по элементам строки или столбца
- •§3. Операции над матрицами
- •§4. Системы линейных алгебраических уравнений (слау). Матричный метод решения
- •§5. Метод Гаусса для исследования и решения слау
- •§6. Однородные системы линейных алгебраических уравнений
- •Глава 2. Элементы векторной алгебры и аналитической геометрии
- •§1. Векторы и линейные операции над ними
- •§2. Базис векторного пространства. Координаты вектора
- •Теорема. При сложении векторов их соответствующие координаты складываются, при умножении вектора на число все его координаты умножаются на это число.
- •§3. Скалярное произведение векторов и его свойства
- •§4. Векторное произведение векторов и его свойства
- •§5. Смешанное произведение векторов
- •§6. Прямая на плоскости
- •§7. Плоскость в пространстве
- •§8. Прямая в пространстве
- •§9. Кривые второго порядка на плоскости
- •§10. Основные понятия об n-мерном арифметическом пространстве
- •Глава 3. Введение в анализ.
- •§1. Функции
- •1.1. Функция. Способы задания функций
- •1.2. Элементарные функции
- •§2. Теория пределов
- •2.1. Последовательность и её предел
- •2.2. Предел функции
- •§3. Бесконечно малые и бесконечно большие функции
- •3.5. Сравнение бесконечно малых
- •§4. Непрерывность функций. Точки разрыва
- •4.1. Непрерывность функции в точке
- •4.2. Классификация точек разрыва
- •Глава 4. Дифференциальное исчисление фуннкций одной переменной
- •§1. Приращения и производные
- •§2. Механический и геометрический смыслы производной
- •§3. Правила дифференцирования
- •§4. Дифференциал функции
- •§5. Производные и дифференциалы высших порядков
- •§6. Правило Лопиталя. Раскрытие неопределенностей
- •§7. Исследование функций с помощью производных
- •7.1. Монотонность и экстремумы функции
- •7.2. Выпуклость и точки перегиба функции
- •7.3. Асимптоты графика функции.
- •7.4. Схема исследования и построения графика функции
- •6. Построение таблицы, в которой указываются все найденные точки разрыва, критические точки первого и второго порядка и интервалы между ними. В каждом интервале характеризуется поведение функции.
- •Глава 5. Функции нескольких переменных
- •§1. Основные понятия о функциях нескольких переменных
- •1.2. Способы задания функции нескольких переменных
- •§2. Дифференцирование функций нескольких переменных
- •2.1. Частные приращения и частные производные
- •2.2. Полное приращение и полный дифференциал
- •§3. Производные и дифференциалы высших порядков
- •§4. Экстремумы функции нескольких переменных
- •Глава 6. Неопределенные и определенные интегралы
- •§1. Первообразная и неопределенный интеграл. Их свойства
- •1.1. Основные определения
- •1.2. Таблица основных неопределенных интегралов
- •§3. Определенный интеграл как предел интегральных сумм
- •§4. Свойства определенного интеграла
- •§5. Несобственные интегралы
- •Глава 7. Обыкновенные дифференциальные уравнения
- •§1. Основные понятия об уравнениях первого порядка
- •§2. Уравнения с разделяющимися переменными
- •§3. Однородные уравнения первого порядка
- •§4. Линейные уравнения первого порядка
- •§5. Основные понятия об уравнениях высшего порядка
- •§6. Линейные дифференциальные уравнения (лду)
- •6.1. Линейные дифференциальные уравнения n-го порядка
- •6.2. Однородные линейные дифференциальные уравнения (олду)
- •6.3. Линейная независимость функций
- •6.4. Общее решение линейного однородного дифференциального уравнения n-го порядка
- •6.5. Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами
- •6.6. Общее решение линейного неоднородного дифференциального уравнения
- •6.7. Линейные дифференциальные уравнения второго порядка с постоянными коэффициентами и специального вида правой частью.
- •Содержание
Глава I. Линейная алгебра
§1. Матрицы. Определители 1-го, 2-го, 3-го порядков. Свойства определителей
Определение.
Матрицей
размера
![]() называется прямоугольная таблица чисел,
состоящая из
называется прямоугольная таблица чисел,
состоящая из
![]() строк и
строк и
![]() столбцов.
столбцов.
Числа стоящие в матрице называются ее элементами и обозначаются переменной (буквой) с двумя индексами, первый из которых равен номеру строки, а второй номеру столбца в пересечении которых находится данный элемент.
Матрица, у которой число строк равно числу столбцов называется квадратной, а это число строк (столбцов) называется ее порядком. Каждой квадратной матрице по определённому правилу сопоставляется число, которое называется определителем этой матрицы.
 .
.
Определителем матрицы 1-го порядка называется элемент этой матрицы.
2)
![]() .
.
3)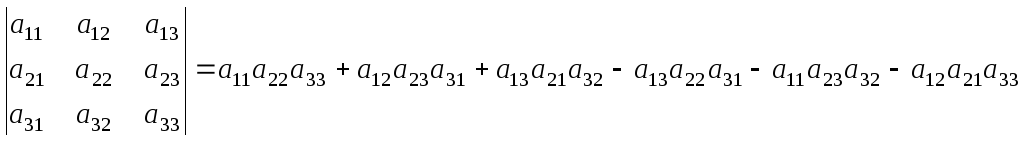 .
.
Это правило называется правилом треугольников (Саррюса).

![]() +
+
+
+
Транспонированной
матрицей
для матрицы
![]() называется матрица
называется матрица![]() ,
столбцами которой являются соответствующие
строки матрицы
,
столбцами которой являются соответствующие
строки матрицы![]() .
.
Свойства определителей:
1) Определители
квадратной матрицы
![]() и транспонированной матрицы
и транспонированной матрицы![]() совпадают, т.е.
совпадают, т.е.![]() .
.
2) При перемене местами двух строк (столбцов) матрицы, её определитель меняет свой знак на противоположный.
3) Определитель матрицы с двумя одинаковыми строками (столбцами) равен 0.
4) Если все элементы
одной строки (столбца)
квадратной матрицы умножить на число
![]() ,
то её определитель умножится на это
число.
,
то её определитель умножится на это
число.
5) Если квадратная матрица содержит нулевую строку (столбец), то её определитель равен 0.
6) Если одна из строк (столбцов) определителя записывается в виде суммы двух строк (столбцов), то определитель записывается в виде суммы двух определителей, у которых на месте этой строки (столбца) стоят соответственно первые и вторые слагаемые. Остальные соответствующие строки (столбцы) всех трёх определителей равны.
7) Если к одной
строке (столбцу)
матрицы прибавить другую её строку
(столбец),
умноженную на число
![]() ,
то определитель матрицы при этом не
изменится.
,
то определитель матрицы при этом не
изменится.
§2. Миноры и алгебраические дополнения. Разложение определителя по элементам строки или столбца
Минором
элемента
![]() матрицы
матрицы![]() называется матрица, полученная из
называется матрица, полученная из![]() путём вычёркивания строки и столбца,
проходящих через элемент
путём вычёркивания строки и столбца,
проходящих через элемент![]() (обозначение:
(обозначение:
![]() ).
Алгебраическим
дополнением
элемента
).
Алгебраическим
дополнением
элемента
![]() называется число
называется число![]() .
Здесь
.
Здесь![]() – определитель минора элемента
– определитель минора элемента
![]() .
.
Теорема о
разложении определителя.
Определитель
матрицы
![]()
![]() - го порядка равен сумме произведений
элементов какой‑либо её выбранной
строки или столбца на их алгебраические
дополнения, т.е.
- го порядка равен сумме произведений
элементов какой‑либо её выбранной
строки или столбца на их алгебраические
дополнения, т.е.![]() .
Здесь
.
Здесь
![]() – номер выбранной строки,
– номер выбранной строки,![]() .
.
Определение.
Определителем
матрицы
![]()
![]() -го
порядка называется число, сопоставляемое
этой матрице с помощью последовательного
применения теоремы о разложении и других
свойств определителей.
-го
порядка называется число, сопоставляемое
этой матрице с помощью последовательного
применения теоремы о разложении и других
свойств определителей.
Диагональная матрица, у которой на главной диагонали стоят только единичные элементы называется единичной матрицей:
E= .
.
Определитель единичной матрицы равен 1, т.е. E=1.
§3. Операции над матрицами
Над матрицами можно производить следующие операции: умножение на число, сложение, умножение матриц и нахождение обратной матрицы. Первые две операции называются линейными.
Определение.
Произведением
матрицы
![]() размера
размера
![]() на число
на число
![]() ,
называется матрица
,
называется матрица
![]() размера
размера![]() ,
каждый элемент
,
каждый элемент![]() которой равен
которой равен![]() .
.
Определение.
Суммой
матриц
![]() и
и![]() одинакового размера называется матрица
одинакового размера называется матрица![]() того же размера
каждый элемент
того же размера
каждый элемент
![]() которой равен
которой равен![]() .
.
Определение.
Произведением строки
A из
![]() элементов на
столбец
B из
элементов на
столбец
B из
![]() элементов называется число
элементов называется число

Определение.
Произведением
матрицы
A размера
![]() на матрицу
B размера
на матрицу
B размера
![]() называется матрица C размера
называется матрица C размера![]() ,
каждый элемент
,
каждый элемент![]() которой равен произведению
которой равен произведению![]() –ой
строки матрицы A на
–ой
строки матрицы A на![]() –ый
столбец матрицы
–ый
столбец матрицы![]() ,
т.
е.
,
т.
е.
![]() .
.
Для любой квадратной матрицы A верно равенство AE=EA=A, то есть единичная матрица играет роль единицы при умножении матриц.
Кроме того, для квадратных матриц верно равенство AB=AB.
Определение. Обратной матрицей для квадратной матрицы A называется такая матрица A-1, что выполняется равенство AA-1=A-1A=E.
Квадратная матрица
A,
определитель которой равен нулю,
называется
вырожденной,
матрица, определитель которой не равен
нулю, называется невырожденной.
Присоединённой
матрицей
для квадратной
матрицы A
называется матрица
![]() ,
элементами которой являются алгебраические
дополнения соответствующих элементов
матрицыA.
,
элементами которой являются алгебраические
дополнения соответствующих элементов
матрицыA.
Теорема об обратной матрице. Невырожденные матрицы и только они имеют обратные матрицы, которые находятся по формуле
![]() .
.
