4. Енергетична характеристика як нелінійний кореляційний зв'язок.

Розглянемо вивід енергетичної характеристики як нелінійного кореляційного зв'язку.

На практиці приходиться зустрічатися з нелінійними кореляційними зв'язками, тобто такими зв'язками, коли приватні середні (дослідні точки) лягають певною подобою біля деякої кривої лінії, а не прямої.

При нелінійній регресії, насамперед, виникає питання визначення сили або тісноти зв'язку між Y і Х, що може бути різноманітною. К. Пірсон, як зазначено вище, запропонував у якості міри нелінійного зв'язку кореляційне відношення (11). До загальних властивостей кореляційного відношення можна додати наступне:

1. Якщо між Y і Х немає кореляційного зв'язку, то кореляційне відношення η дорівнює нулю і якщо зв'язок функціональний, то кореляційне відношення дорівнює одиниці.

2. Якщо ж, η=0 то Y не пов’язано з Х однозначним кореляційним зв'язок.

Ці дві властивості з’ясовують зміст крайніх значень кореляційного відношення. Сенс його проміжних значень пояснюється з тотожності:

(12)

Вона вказує, що при наближенні η до одиниці середня дисперсія Y по стовпчиках зменшується, наближаючись до нуля, а це показує, що зв'язок між Y і Х стає більш тіснішим. Це показує, що η дійсно є мірою кореляційного зв'язку будь-якого за формою. В цьому полягає велика перевага кореляційного відношення перед коефіцієнтом кореляції, що служить лише мірою лінійного кореляційного зв'язку.

В ряді випадків теоретичні і дослідні дані дозволяють припустити форму кривої, по якій можна зробити вимірювання, по методу найменших квадратів, приватних середніх щодо даної кривої.

Розглянемо загальний випадок параболічної залежності між Y і Х.

Звичайно парабола має вид:

Y=а₀+а₁∙х²+…+а_р∙х^р, (13)

і шукається за методом найменших квадратів. Коефіцієнти рівняння (13) визначаються таким чином, щоб сума:

оберталася в мінімум для знайдених значень.

Тоді повинні мати місце:

…

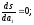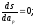
Ці рівняння легко приводяться до виду:

а₀∑п_х+а₁∑п_х∙х+…+ а_р∑п_х∙х^р=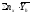

а₀∑п_х∙х+а₁∑п_х∙х²+…+ а_р∑п_х∙х^р+1=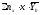

а₀∑п_х∙х^р+а₁∑п_х∙х^р+1+…+ а_р∑п_х∙х^2р=

Тут:

п_х=п_h – число відліків при даному Х=х_h;

- приватні середні (дослідні точки).

Вирішуючи цю систему знаходимо значення шуканих коефіцієнтів а₀, а₁, а₂…а_р, що звертають суму S в мінімум.

Поклавши в рівняння (13) Y=ω, а Х=1/А або одержимо загальний випадок гіперболічної залежностіω=f(А), тобто питомої витрати електроенергії від випуску продукції як нелінійного кореляційного зв’язку.

5. Оцінка статистичних характеристик кореляційної моделі. Оцінка її похибки.

5.1. Оцінка коефіцієнта кореляції.

При обсязі вибірки коефіцієнт кореляції має, приблизно, стандарт (середньоквадратичне відхилення):

(14)

Прийнявши за r₀ значення коефіцієнта кореляції генеральної сукупності, стосовно котрого дослідні дані можна вважати випадковою вибіркою, то з більшою можливістю можна думати, що численні значення між r₀ і r менше 3σ_r.

Часто при невеличкому числі спостережень або при малому значенні коефіцієнта кореляції припадає сумнів у реальності зв’язку між досліджуваними ознаками. У цьому випадку виникає питання, чи не випадково значення коефіцієнта кореляції відрізняється від нуля і чи не дорівнює він у дійсності нулю. Це питання вирішується рівнянням коефіцієнта кореляції з його стандартом, причому коли коефіцієнт кореляції дорівнює нулю, його стандарт дорівнює:

(15)

Саме, якщо:

(16)

можна вважати коефіцієнт кореляції значущим і зв'язок реальним.