ЛЕКЦИЯ_5. МАТЕМАТИЧЕСКОЕ ОПИСАНИЕ

Автоматических систем

СОДЕРЖАНИЕ.

5.1 Основные способы математического описания.Уравнения движения.

5.2 Примеры уравнений объектов управления

5.2.1 Гидравлический резервуар

5.2.2 Электрическая емкость

5.2.3 Химический реактор полного перемешивания

5.3 Определение линейной стационарной системы

5.4 Динамическое поведение линейных системы

5.5 Динамические процессы в системах

5.6 Переходная и весовая функции

5.7 Интеграл дюамеля

5.8 Преобразование Лапласа

5.8.1 Определение преобразования Лапласа

5.1 Основные способы математического описания.Уравнения движения.

мает постоянное значение y = y₀ и уравнение (1) преобразуется к виду:

(2)

Конечное уравнение (2) является уравнением статики. Статический режим можно характеризовать с помощью статических характеристик.Статической характеристикой объекта (системы) называется зависимость выходной величины от входной в статическом режиме.Статическую характеристику можно построить экспериментально, если подавать на вход объекта постоянные воздействия и замерять выходную переменную после окончания переходного процесса. Если объект имеет несколько входов, то он характеризуется семейством статических характеристик. В свою очередь, сама статическая характеристика характеризуется коэффициентом k, который определяется как k= dy/dx. Для объектов с нелинейной статической характеристикой коэффициент усиления является переменной величиной, для объектов же с линейными статическими характеристиками коэффициент усиления – величина постоянная (рис. 5.1).

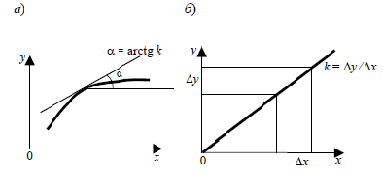
Рис. 5.1 Статическая характеристика объектов:

а – нелинейного; б – линейного

5.2 Примеры уравнений объектов управления

В теории автоматического управления широко используется метод математических аналогий, согласно которому различные по физической природе объекты описываются однотипными математическими зависимостями.

Рассмотрим некоторые примеры составления уравнений статики и динамики для различных по физической природе объектов( в том числе примеры судовых систем)

1. Электропривод якорно-швартового устройства

2.САР напряжения генератора (система токового компаундирования

3. Авторулевой, удерживающий судно на заданном курсе с требуемой точностью в условиях волнения моря и других возмущающих сигналах.

4 .Электропривод траловой лебедки, обеспечивающий требуемые усилия и скорость выборки трала в условиях переменной нагрузки на ваерах, волнения моря, действия течений.

5. Холодильная автоматика, обеспечивающая поддержание заданной температуры в камерах в условиях изменяющегося притока тепла.

5.2.1 Гидравлический резервуар

Примером простейшего объекта автоматического управления является гидравлический резервуар, в котором имеется приток и сток жидкости. Принципиальная и структурная схемы представлены на рис. 5.2.

Основной координатой, характеризующей состояние рассматриваемого объекта, является уровень жидкости Н, который выбирается в качестве выходной регулируемой величины. Входным и соответственно регулирующим воздействием является скорость притока воды в резервуар Q, внешним возмущением – расход воды из резервуара G. При постоянной степени открытия дросселя на притоке жидкости, уровень

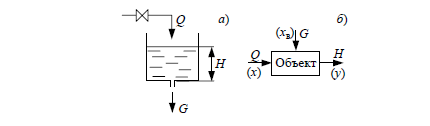
Рис. 5.2 Гидравлическая емкость:

а – принципиальная схема; б – структурная схема

определяется разностью (Q – G). По условиям работы объекта величина притока Q изменяется произвольно во времени. Уравнение динамики, описывающее зависимость уровня H в переходном режиме от Q, в соответствии с законом гидравлики записывается в виде

(3)

где S – площадь поперечного сечения резервуара.

Уравнение (3) представляет собой математическое описание объекта регулирования – гидравлической емкости и является обыкновенным дифференциальным уравнением 1-го порядка.