1.7 Исследование систем линейных алгебраических уравнений

В предыдущих параграфах мы выяснили, что система линейных уравнений снеизвестными может иметь единственное решение, может иметь бесчисленное множество решений (неопределенная), может не иметь ни одного решения (несовместная), и познакомились с некоторыми методами решения таких систем.

Например, система не имеет решений, т.е. несовместна;

система имеет единственное решение

системаимеет бесчисленное множество решений при

Напомним, что прежде чем решать систему уравнений, имеет смысл исследовать эту систему, т.е. выяснить ответы на следующие вопросы:

1) Совместна ли система?

2) Если система совместна, то, сколько решений она имеет – одно или несколько?

3) Как найти все решения системы?

Для систем уравнений малой размерности при ответы на эти вопросы можно получить, пользуясь формулами Крамера:

1) если основной определитель системы то система совместна и имеет единственное решение, которое можно найти по формулам Крамера;

2) если а хотя бы один из вспомогательных определителей то система несовместна, т.е. не имеет решений;

3) если же и все, а хотя бы один из коэффициентов системы уравненийто система неопределенная и имеет бесчисленное множество решений.

Сложнее решаются вопросы исследования и решения системы уравнений с большим количеством уравнений и неизвестных, особенно в случае.

Легко разрешить эти вопросы можно с помощью понятия ранга матрицы.

1. Ранг матрицы и его свойства

В существующей математической литературе можно выделить несколько подходов к определению понятия ранга матрицы:

- с помощью понятия линейной зависимости/независимости строк (столбцов) матрицы (ранг равен максимальному количеству линейно независимых строк (столбцов) матрицы);

- с помощью понятия минора матрицы как наивысший порядок минора, отличного от нуля (минором матрицы порядка называется определитель – го порядка, который составлен из элементов, стоящих на пересечении вычеркиваемыхстрок истолбцов матрицы);

- с помощью метода Гаусса (по завершении прямого хода ранг матрицы равен количеству ненулевых строк).

Ранг матрицы обозначают

Часто нахождение ранга облегчает применение его свойств:

1. Квадратная невырожденная матрица всегда имеет ранг, отличный от нуля.

2. При транспонировании ранг матрицы не изменяется.

3. При перестановке двух параллельных рядов матрицы (двух строк или двух столбцов) ранг матрицы не изменяется.

4. При удалении нулевого столбца или нулевой строки ранг матрицы не изменяется.

5. При удалении строки (или столбца), которая является линейной комбинацией других строк (или столбцов), ранг матрицы не изменяется.

6. При умножении всех элементов строки (столбца) на число 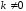ранг матрицы не изменяется.

7. Ранг матрицы не превосходит меньшего из ее размеров, т.е.

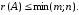
8. тогда и только тогда, когда все элементы матрицы равны нулю.

Пример 1.

Пример 2.

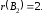
Пример 3.

Ранг матрицы определен на основании свойства определителя, содержащего строки с пропорциональными элементами. (Любой минор 2-го или 3-го порядка матрицы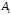равен нулю).

Ранги матриц и определены с помощью вычеркивания нулевых строк. (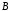матрицеминор на пересечении двух первых строк и двух первых столбцов отличен от нуля).

Матрица – невырожденная, поэтому ее ранг равен трем. (Проверьте самостоятельно условие).

Ранг матрицы определим с помощью элементарных преобразований:

1) элементы первой строки умножим на (-2) и прибавим к элементам 2-й строки;

2) элементы первой строки умножим на (-1) и прибавим к элементам третьей строки;

3) элементы первой строки умножим на (-5) и прибавим к элементам четвертой строки:

Третью строку полученной матрицы прибавим ко второй и к четвертой строкам

(Удалены строки 2 и 4 с нулевыми элементами). Число ненулевых строк равно 2 или минор 2-го порядка в левом углу матрицы

, что и требовалось доказать.

2. Теорема Кронеккера-Капелли (о разрешимости СЛАУ)

Вопрос о разрешимости системы линейных алгебраических уравнений в общем виде рассматривается в следующей теореме.

Теорема Кронеккера-Капелли.

Чтобы система линейных уравнений была совместной, необходимо и достаточно, чтобы ранг матрицы этой системы был равен рангу ее расширенной матрицы.

Не проводя строго доказательства теоремы, поясним его. В процессе преобразования системы уравнений (6.1) к виду (6.3) с помощью элементарных преобразований ранги матрицы системы 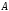и расширенной матрицы не изменяются. В п. 1.6 было установлено, что система уравнений (6.3) совместна тогда и только тогда, когда все свободные члены 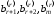равны нулю. В этом случае ранг матрицы и ранг расширенной матрицы системы (6.1) совпадают (оба равны).

Для совместных систем линейных уравнений справедлива следующая теорема.

Теорема о числе решений системы.

Пусть ранг матрицы, составленной из коэффициентов системы линейных уравнений, равен рангу расширенной матрицы. Тогда, если (– число неизвестных системы), то система имеет единственное решение; если, то система имеет бесчисленное множество решений.

В случае определенности СЛАУ для ее решения подходит любой из трех методов: Крамера, Гаусса, матричный.

Если же система не определена, тогда некоторым неизвестным, которые называются свободными, можно придавать произвольные значения, а неизвестных, называемых главными (базисными), определяются через свободные единственным образом. При этом базисными переменными выбираются те, для которых определитель матрицы, составленный из коэффициентов при них, отличен от нуля. Полученные выражения главных переменных через свободные объявляются решением системы.

Например, исследуем и решим систему:

Составим расширенную матрицу системы и будем приводить ее к ступенчатому виду методом Гаусса, в итоге определим ее ранг, а ранг основной матрицы системы определим, «закрыв» столбец правых частей.

Ответ: система не совместна.

Рассмотрим пример СЛАУ Составим основную матрицу системы и найдем ее ранг.

Составим расширенную матрицу системы и найдем ее ранг:

система совместная, система неопределенная. Решим систему методом Гаусса. Преобразования расширенной матрицы системы приводят к системе уравнений вида

, значит, в качестве главных переменных можно выбрать и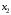, а в качестве свободных – неизвестныеи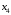. Запишем систему уравнений в виде:

Обратным ходом находим:

Из 1-го уравнения

Ответ: система неопределенная.

3. Исследование однородной СЛАУ

Напомним, что в однородной системе линейных алгебраических уравнений все правые части равны нулю:

Ее расширенная матрица системы отличается от основной наличием лишь нулевого столбца, что по свойству ранга, его не меняет. Следовательно, и по тереме Кронеккера-Капелли однородная СЛАУ совместна всегда.

Этот факт верен еще и потому, что по крайней мере один (нулевой) набор значений неизвестных обращает в тождество каждое уравнение системы.

Таким образом, для однородной системы остается выяснить, определена она или не определена.

В случае 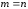справедлива следующаятеорема:

Линейная однородная система уравнений снеизвестными имеет единственное (нулевое) решение тогда и только тогда, когда основной определитель системы, и множество ненулевых решений тогда и только тогда, когда.

Например: .

Решаем методом Гаусса:

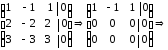Вместо 3-х уравнений получаем одно которое допускает множество решений.

Общее решение: – любые действительные числа.

Положив, получаем одно частное решение:Положив, получаем второе частное решениеи т.д.

Другой пример:

Система совместна, определена, решение:

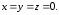
Вопросы для самоконтроля

1. Сформулируйте понятие определителя 2-го порядка, правила его вычисления, свойства.

2. Как определяется детерминант 3-го порядка. Понятие об определителях произвольного порядка. В чем состоит правило треугольника и правило Сарруса вычисления определителя 3-го порядка.

3. Дайте определение минора, алгебраического дополнения элемента. Приведите правило вычисления определителя разложением по элементам ряда.

4. Объясните понятие матрицы, укажите виды матриц. Разъясните линейные операции над матрицами, умножение матриц.

5. Дайте понятие матрицы, обратной данной, приведите алгоритм её нахождения.

6. Дайте понятие о системах линейных алгебраических уравнений снеизвестными, приведите общую схему исследования.

7. Ознакомьтесь с понятием ранга матрицы и методами его вычисления.

8. Сформулируйте условие совместности СЛАУ (теорема Кронеккера-Капелли).

9. Приведите решение системы линейных алгебраических уравнений с помощью формул Крамера, укажите условия применимости.

10. Рассмотрите решение системы линейных алгебраических уравнений средствами матричного исчисления.

11. Что представляют собой элементарные преобразования СЛАУ. Приведите алгоритм метода Гаусса решения СЛАУ.

12. Укажите иные применения метода Гаусса в линейной алгебре.

13. Дайте понятие основных и свободных неизвестных. Приведите алгоритм решения неопределенной СЛАУ.

14. Приведите схему исследования однородных систем линейных уравнений.

Примеры: