- •Высшая математика
- •Элементы линейной алгебры
- •Содержание
- •Введение
- •Тематический план
- •Элементы линейной алгебры
- •1.1 Понятие системы линейных алгебраических уравнений (слау)
- •1.4 Матрицы и действия над ними
- •1.4.1 Понятие матрицы
- •1.4.2 Алгебраические операции над матрицами
- •Найдем матрицу
- •1.6 Метод Гаусса (метод последовательного исключения неизвестных)
- •1.7 Исследование систем линейных алгебраических уравнений
- •[4], № 387-390, 414-417, 435-437, 441-443, 446-451;
- •[5], Задачи 15.4, 15.11, 15.14, 15.23;
- •[7], № 586-601, 605-610, 611-622, 624-629.
- •Список использованной и рекомендуемой литературы
- •98309, Керчь, ул. Орджоникидзе, 82
1.4.2 Алгебраические операции над матрицами
Сложение матриц.
Матрицы одинаковой размерности можно почленно складывать.
Суммой
двух матриц
 и
и одинаковой размерности
одинаковой размерности называется матрица
называется матрица той
же размерности, элементы которой,
той
же размерности, элементы которой,
 где
где
 .
.
Например,
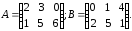
Тогда
 .
.
Свойства сложения матриц:
1.
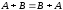 (коммутативность).
(коммутативность).
2.
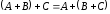 (ассоциативность).
(ассоциативность).
3.
Если
 ,
то
,
то
2)
Вычитание
матриц
определяется аналогично сложению. Если
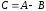 ,
то
,
то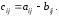
В приведенном выше примере
 .
.
3) Умножение матрицы на число.
Произведением
матрицы
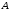 на число
на число называют
матрицу
называют
матрицу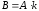 ,
элементы которой
,
элементы которой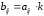 ,
где
,
где .
.
Например,
 ,
,

Найдем матрицу
 .
.
Свойства умножения матриц на число:
1.

2.

3.

4) Умножение матриц.
Умножение
двух
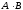 матриц определено, если число (количество)
столбцов первой матрицы
матриц определено, если число (количество)
столбцов первой матрицы равно числу строк второй матрицы
равно числу строк второй матрицы .
Такие матрицы называютсясоответственными.
.
Такие матрицы называютсясоответственными.
Пусть
размерность матрицы
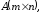 а матрицы
а матрицы .
.
Произведением
двух матриц
 и
и называется матрица
называется матрица ,
элементыкоторой
определяются по формуле:
,
элементыкоторой
определяются по формуле:
 ,
т.е. каждый элемент матрицы
,
т.е. каждый элемент матрицы есть сумма произведений элементов
есть сумма произведений элементов -й строки матрицы
-й строки матрицы на
на -й
столбец матрицы
-й
столбец матрицы .
.
При
этом размерность матрицы будет равна
будет равна .
.
Например,
пусть


Размерности
матриц
 Число
столбцов матрицы
Число
столбцов матрицы

 ,
число строк матрицы
,
число строк матрицы

 .
Найдем произведение
.
Найдем произведение

Свойства произведения матриц:
1.
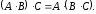
2.
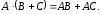
3.

4.

5.
Произведение двух матриц в общем случае
не коммутативно. Не всегда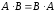 .
Эти произведения могут быть разными
матрицами (и с разными элементами, и
разной размерности), а могут после
перестановки и вовсе не существовать.
Например в рассмотренном примере
матрицу
.
Эти произведения могут быть разными
матрицами (и с разными элементами, и
разной размерности), а могут после
перестановки и вовсе не существовать.
Например в рассмотренном примере
матрицу нельзя умножить на матрицу
нельзя умножить на матрицу .
.
6.
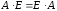
7.

Возведение матрицы в степень.
Эта
операция определяется только для
квадратных матриц и только для целых
степеней
 .
.
Целой
положительной степенью
 квадратной матрицы
квадратной матрицы называется
произведение
называется
произведение матриц, равных
матриц, равных .
.

Принято
считать .
.
Обращение матрицы.
Для
матриц операция деления не определена,
но можно определить аналог типа
 – нахождениеобратной
к данной.
– нахождениеобратной
к данной.
Матрица
 называется
обратной
к матрице
называется
обратной
к матрице ,
если
,
если
 .
.
Обратная
матрица обозначается ,
т.е.
,
т.е. .
.
Обратная
матрица существует только для квадратной
матрицы, если ее определитель .
.
Действительно,
т.к. ,
то
,
то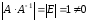 .
.
С
другой стороны,
Следовательно,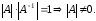
Каждая
квадратная матрица
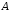 с определителем, отличным от нуля, имеет
обратную. Ее элементы находят по формуле
с определителем, отличным от нуля, имеет
обратную. Ее элементы находят по формуле .
.
Вычисление
обратной матрицы
 и есть операция обращения матрицы.
и есть операция обращения матрицы.
Алгоритм вычисления обратной матрицы:
1. Найти определитель исходной матрицы.
Если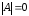 ,
то
,
то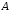 – вырожденная матрица, обратная матрица
– вырожденная матрица, обратная матрица не существует и вычисление нужно
прекратить.
не существует и вычисление нужно
прекратить.
Если ,
то обратная матрица существует. Перейти
к п.2.
,
то обратная матрица существует. Перейти
к п.2.
2.
Найти алгебраические дополнения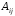 каждого
элемента матрицы
каждого
элемента матрицы
 и составить матрицу из алгебраических
дополнений в порядке следования элементов
матрицы.
и составить матрицу из алгебраических
дополнений в порядке следования элементов
матрицы.
3. Транспонировать матрицу из алгебраических дополнений.
4.
Полученную матрицу умножить на множитель
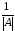 (или иначе: каждый элемент полученной
матрицы разделить на определитель
матрицы
(или иначе: каждый элемент полученной
матрицы разделить на определитель
матрицы ).
В результате получим обратную матрицу
).
В результате получим обратную матрицу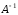 .
.
5.
Выполнить проверку правильности
вычислений, перемножив матрицы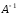 и
и в
прямом и обратном порядке. Получение в
результате единичной матрицы служит
критерием правильности вычислений,
т.е.
в
прямом и обратном порядке. Получение в
результате единичной матрицы служит
критерием правильности вычислений,
т.е.
 .
.
Пример.
Найти матрицу, обратную данной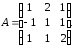
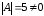 -
обратная матрица существует.
-
обратная матрица существует.


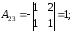
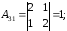


Составим
матрицу из :
:

3.
Транспонируем матрицу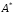 :
:

4.
 ,
т.е.
,
т.е.

5. Проверку предлагается выполнить самостоятельно.
Матричный способ решения СЛАУ
Введенные нами операции над матрицами позволяют:
предложить матричную форму записи СЛАУ.
Для
этого матрицу, составленную из
коэффициентов при неизвестных системы
 линейных
уравнений с
линейных
уравнений с
 неизвестными
неизвестными
 ,
назовем основной
матрицей системы.
,
назовем основной
матрицей системы.
Ее
размерность
 .
.
Основная матрица системы, дополненная столбцом свободных членов, называется расширенной матрицей системы. Она имеет вид:
 ,
ее размерность
,
ее размерность
 .
.
Обозначим
матрицу – столбец, элементы которой –
неизвестные системы, через
 (ее размерность
(ее размерность ),
а матрицу – столбец, элементы которой
– свободные члены системы,
),
а матрицу – столбец, элементы которой
– свободные члены системы, (ее размерность
(ее размерность ):
):


Тогда
систему уравнений можно записать в
матричной форме:
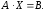
получить еще один способ решения СЛАУ для случая
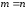 с невырожденной матрицей системы,
который называетсяматричным
способом.
В случае
с невырожденной матрицей системы,
который называетсяматричным
способом.
В случае
 существует обратная матрица
существует обратная матрица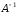 .
Запишем систему в матричной форме:
.
Запишем систему в матричной форме:

Умножим
слева обе части равенства на
 .
Получим:
.
Получим:
 .
.
На основании свойств произведения матриц и определения обратной матрицы преобразуем левую часть равенства:
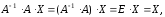
где
 –
матрица–столбец из неизвестных системы.
Тогда решение системы уравнений имеет
вид:
–
матрица–столбец из неизвестных системы.
Тогда решение системы уравнений имеет
вид:
Пример.
Решить систему уравнений матричным
способом: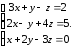
Запишем
для данной системы уравнений матрицы :
:



Для
нахождения обратной матрицы
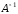 найдем
основной определитель системы
найдем
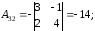
основной определитель системы и алгебраические дополнения каждого
элемента матрицы
и алгебраические дополнения каждого
элемента матрицы :
:









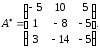
Составим матрицу из алгебраических дополнений
 Транспонируем
ее
Транспонируем
ее .
.
Найдем

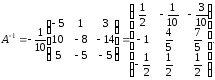

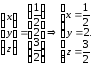
Ответ: