1.4 Матрицы и действия над ними

1.4.1 Понятие матрицы

Значительная часть математических моделей объектов из различных областей науки и практики описывается в достаточно простой и компактной форме с помощью матриц. В частности, в линейной алгебре матрицы используются для формализованной записи СЛАУ и поиска их решений в случае, когда теория определителей неприменима.

Впервые матрицы упоминались ещё в древнем Китае, называясь тогда «волшебным квадратом». Также «волшебные квадраты» были известны чуть позднее у арабских математиков, примерно тогда появился принцип сложения матриц. Основным применением матриц было решение линейных уравнений. Поглощенные развитием теории определителей в конце 17-го века, математики долгое время рассматривали результат расположения элементов в виде квадратной таблицы как число, отвлекаясь от формы записи элементов. Только в 1850 г. Джеймсом Сильвестром был введен сам термин «матрица» для обозначения прямоугольной таблицы чисел, которую он не мог уже назвать определителем. Основной работой, в которой матрицы были представлены как абстрактные объекты, стал «Мемуар о теории матриц» Артура Кэли 1858 г.

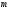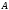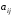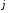Определение. Прямоугольная таблица объектов какой-либо природы (изначально чисел), состоящая из строк истолбцов, называетсяматрицей размера (читается «на»). Числа, образующие матрицу, называют элементами матрицы. Матрицы обозначают заглавными буквами латинского алфавита, их элементы – строчными буквами с двойным индексом. Так, например, матрица _, составленная из элементов ( – номер строки; - номер столбца), имеет вид:

_{Символически элементы матрицы записывают в} виде

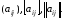
Элементы, имеющие одинаковые индексы, стоят на главной диагонали (т.е. главная диагональ начинается в левом верхнем углу матрицы). Диагональ, идущая из правого верхнего угла матрицы, называется побочной.

Если , матрицапрямоугольная.

Если 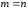, то матрица называется квадратной, а число задает ее порядок.

Определитель-го порядка можно считать характеристикой квадратной матрицы и обозначать,

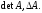
Если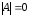, то квадратная матрица называетсявырожденной (особенной), если -невырожденной.

Рассмотрим основные виды матриц:

- матрица-скаляр ;

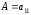- матрица-строка , ее размерность;

- матрица-столбец , ее размерность;

- нулевая матрица (нуль-матрица) – матрица любой размерности, все элементы которой равны нулю ;

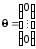- трапециевидная – прямоугольная матрица, у которой под или над главной диагональю стоят нули;

- треугольная – квадратная матрица, у которой под или над главной диагональю стоят нули;

- диагональная – квадратная матрица, у которой среди элементов, стоящих на главной диагонали, есть отличные от нуля, остальные же равны нулю;

- единичная ( или )- диагональная матрица, у которой все диагональные элементы равны единице.

Например, - единичная матрица 2-го порядка.

Для матриц определено отношение равенства. Две матрицы и называются равными, если они имеют одинаковую размерность и элементы с соответствующими индексами равны . Пишут: .

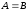Кроме того, определена операция транспонирования.

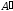Матрица, у которой строки меняются местами со столбцами с сохранением порядка, называется транспонированной по отношению к матрице размерности и обозначается или. Ее размерность.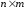

Заметим, что операция транспонирования оставляет диагональные элементы на местах, а остальные отображаются симметрично главной диагонали.

Например,

Свойства операции транспонирования: