
- •Высшая математика
- •Элементы линейной алгебры
- •Содержание
- •Введение
- •Тематический план
- •Элементы линейной алгебры
- •1.1 Понятие системы линейных алгебраических уравнений (слау)
- •1.4 Матрицы и действия над ними
- •1.4.1 Понятие матрицы
- •1.4.2 Алгебраические операции над матрицами
- •Найдем матрицу
- •1.6 Метод Гаусса (метод последовательного исключения неизвестных)
- •1.7 Исследование систем линейных алгебраических уравнений
- •[4], № 387-390, 414-417, 435-437, 441-443, 446-451;
- •[5], Задачи 15.4, 15.11, 15.14, 15.23;
- •[7], № 586-601, 605-610, 611-622, 624-629.
- •Список использованной и рекомендуемой литературы
- •98309, Керчь, ул. Орджоникидзе, 82
Тематический план
Тема «Элементы линейной алгебры»
Понятие системы линейных алгебраических уравнений (СЛАУ).
Решение СЛАУ размера 2x2.
Понятие определителя 2-го порядка.
Свойства определителя.
Формулы Крамера решения СЛАУ.
Решение СЛАУ размера 3x3.
Понятие определителя 3-го порядка.
Методы его вычисления (правило треугольника, правило Сарруса, правило Лапласа).
Понятие об определителе произвольного порядка.
Понятие матрицы.
Математические операции над матрицами.
Матричный способ решения СЛАУ.
Метод Гаусса (метод последовательного исключения неизвестных).
Понятие ранга матрицы.
Исследование систем линейных алгебраических уравнений.
Элементы линейной алгебры
1.1 Понятие системы линейных алгебраических уравнений (слау)
Изначально
линейная алгебра рассматривала вопросы
о решении линейных
уравнений,
т.е. таких, где левая часть составлялась
из переменных в первой степени и к ним
применялись линейные операции: умножение
на постоянное число (константу); сложение.
В качестве правых частей брались
константы. В результате получались
уравнения вида:
 (с одной неизвестной),
(с одной неизвестной),
 (с
двумя неизвестными). Эти уравнения имеют
довольно простую геометрическую
интерпретацию – оба задают прямые линии
на плоскости.
(с
двумя неизвестными). Эти уравнения имеют
довольно простую геометрическую
интерпретацию – оба задают прямые линии
на плоскости.
Если
неизвестных
(переменных)
в уравнении несколько, то для их
обозначения удобно использовать индексы
и обозначать:
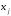 (читается «икс житое (йотое)), где
(читается «икс житое (йотое)), где определяется количеством переменных,
например, при
определяется количеством переменных,
например, при неизвестных
неизвестных .
.
Коэффициенты
при неизвестных
принято обозначать буквами с двойным
индексом:
 (читается «а и житое»), где
(читается «а и житое»), где
 -
номер уравнения,
-
номер уравнения,
 -
номер переменной, перед которой стоит
коэффициент. Константы, стоящие в правых
частях уравнений, называются свободными
членами системы
и обозначаются
-
номер переменной, перед которой стоит
коэффициент. Константы, стоящие в правых
частях уравнений, называются свободными
членами системы
и обозначаются
 .
.
Тогда,
система
 линейных
алгебраических уравнений с
линейных
алгебраических уравнений с
 неизвестными (СЛАУ размера
неизвестными (СЛАУ размера )
имеет следующий вид:
)
имеет следующий вид:
 .
(1.1)
.
(1.1)
Если среди свободных членов системы (1.1) есть отличные от нуля, то система уравнений называется неоднородной, в противном случае однородной:
 .
(1.2)
.
(1.2)
Совокупность

 чисел
чисел называетсярешением
системы (1.1), если после замены неизвестных
называетсярешением
системы (1.1), если после замены неизвестных
 соответственно числами
соответственно числами каждое уравнение системы (1.1) превращается
в тождество (верное равенство).
каждое уравнение системы (1.1) превращается
в тождество (верное равенство).
Система уравнений, не имеющая ни одного решения, называется несовместной.
Система уравнений, имеющая хотя бы одно решение, называется совместной.
Система уравнений, имеющая более одного решения, называется неопределенной.
Система уравнений, имеющая единственное решение, называется определенной.
«Решить систему» означает «найти решение или доказать, что его нет».
При решении любой СЛАУ нужно ответить на 3 вопроса (исследовать СЛАУ):
совместна система или нет;
если совместна, сколько решений она имеет (одно или множество);
как найти все решения системы (указать методы решения СЛАУ).
Изучение
систем линейных уравнений было начато
Лейбницем около 1678 г.; он использовал
индексы в случае системы 3-х уравнений
с 2-мя неизвестными. Лейбниц исключал
обе неизвестные и в результате они
определялись
с
помощью выражения специального вида,
обращение в ноль которого было условием
разрешимости системы. Такое выражение
Лейбниц предложил называть определителем.
Позднее, в 1748 г. Маклорен получил явные
формулы для решения систем в случаях
Рассмотрим систему двух линейных уравнений с двумя неизвестными:
Решением
этой системы уравнений является пара
чисел
Для
нахождения решения применим метод
алгебраического сложения с последующим
исключением неизвестных. Для получения
Вычтем почленно из 1-го уравнения второе:
т.е.
Полагая
выражение
Аналогично,
исключая из системы уравнений
Непосредственной
проверкой легко убедиться, что
полученные значения
Определение.
Выражение
Если
элементы
Определитель
2-го порядка имеет 2 строки и 2 столбца,
которые называются рядами,
следовательно, порядок
определителя
равен количеству его строк или столбцов.
Говорят, элементы с одинаковыми
индексами
Таким образом, определитель 2-го порядка равен разности произведений элементов, стоящих на главной и побочной диагоналях. Это практическое правило вычисления определителя 2-го порядка. Примеры вычисления определителей 2-го порядка:
1.2.2 Формулы Крамера решения СЛАУ
Приняв
введенное нами понятие определителя
2-го порядка, замечаем, что числители
в формулах для нахождения
Легко
заметить, что вспомогательный
определитель
Тогда
формулы для нахождения решения исходной
системы линейных уравнений принимают
следующий вид:
Впервые в таком виде они были записаны Крамером в 1754 г., поэтому носят название формул Крамера для системы двух линейных уравнений с двумя неизвестными.
Замечание:
часто в случае СЛАУ небольших размеров
При решении подобных систем могут быть следующие случаи. 1)
Например,
2)
Например,
3)
Например,
Система несовместна, т.е. не имеет решений.
1.2.3 Свойства определителя
Приведем основные свойства определителя 2-го порядка. 1) Определитель не изменится, если его строки поменять местами с соответствующими столбцами. Эта операция называется транспонированием определителя и фактически означает симметрию относительно главной диагонали.
2) При перестановке двух соседних параллельных рядов определитель изменит знак на противоположный, сохраняя абсолютную величину.
3) Определитель с двумя одинаковыми строками (или столбцами) равен нулю.
4) Общий множитель всех элементов строки (или столбца) можно выносить за знак определителя.
5) Если какие-либо два соседних ряда определителя пропорциональны, то он равен нулю.
6) Если все элементы какой-либо строки (или столбца) равны нулю, то и определитель равен нулю.
7) Если каждый элемент какого-то ряда представляет собой сумму двух (конечного числа) слагаемых, то определитель может быть представлен в виде суммы двух (конечного числа) определителей.
8) Если к какой-либо строке (или столбцу) определителя прибавить соответствующие элементы другой строки (или столбца), умноженные на одно и то же число, то определитель не изменит своей величины.
1.3.1 Понятие определителя 3-го порядка
Пусть
мы имеем систему 3-х линейных уравнений
с 3-мя неизвестными
Аналогично СЛАУ с двумя неизвестными, ее решение может быть найдено в ходе последовательного исключения неизвестных (в силу громоздкости вычислений мы их не приводим).
Для
полученных выражений может быть
введено понятие определителя
3-го порядка, для
обозначения которого также используется
символ
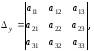
Тогда, основной и вспомогательные определители системы будут иметь вид:
Считая
Заметим: 1)
2) Все свойства определителей 2-го порядка относятся и к определителям 3-го порядка. Например,
3)
Аналогичные формулы имеют место для
систем уравнений с большим числом
неизвестных, следовательно, можно
ввести понятие определителя
произвольного (
1.3.2 Понятие определителя произвольного порядка
Аналогично
определителям 2-го и 3-го порядка можно
составить определитель
Анализируя формулы для вычисления, можно заметить, что определитель 2-го порядка состоит из 2-х слагаемых, каждое из которых содержит по 2 сомножителя, для определителя 3-го порядка эти цифры составляют 6 и 3 соответственно.
Рассуждая
по индукции, получаем, что число
сомножителей, входящих в каждое
произведение, равно порядку определителя,
а количество самих слагаемых равно
Для определителя произвольного порядка остаются верными свойства 1 - 8, выведенные нами для определителя 2-го порядка. 4) Получим из определения детерминанта 3-го порядка правила его вычисления.
1.3.3 Методы вычисления определителя 3-го порядка
1.3.3.1 Правило треугольника
При
решении СЛАУ
Это выражение мы назвали определителем 3-го порядка и обозначили
Заметим, что оно состоит из 6-ти слагаемых, каждое из которых содержит 3 сомножителя, взятых с определенным знаком, причем эти сомножители берутся из разных строк и столбцов. Первые три слагаемые (со знаком «+») составлены как произведение элементов главной диагонали и 2 произведения элементов, стоящих в вершинах треугольников, построенных так, что одна из сторон каждого из них параллельна главной диагонали. Вторые 3 слагаемые (со знаком «-») построены аналогично для вспомогательной диагонали определителя. Эта формула называется Правилом треугольника. Например, вычислим, пользуясь правилом треугольника, определитель:
1.3.3.2 Правило Сарруса Фактически оно представляет собой модификацию правила треугольника и состоит в том, что исходный определитель «расширяется» путем приписывания к нему справа 1-го и 2-го столбцов (либо снизу 1-й и 2-й строк). Далее, 3 члена, являющиеся произведениями 3-х элементов в направлении главной диагонали, начиная от элементов верхней строки определителя, выписываются со знаком «+», а 3 члена, являющиеся произведениями 3-х элементов в направлении побочной диагонали, начиная от элементов нижней строки определителя, выписываются со знаком «-».
Например,
1.3.3.3 Правило Лапласа (Правило разложения определителя по элементам ряда)
Заметим,
что в выражении определителя 4-го
порядка выписывается 4!=24 слагаемых,
состоящих из 4-х сомножителей каждое,
что, естественно, затрудняет процесс
вычисления. Следовательно, возникает
необходимость в получении некой
универсальной формулы вычисления
определителя
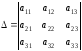
Минором
элемента
Минор
элемента
Алгебраическим
дополнением элемента
Например,
для
Обратимся
вновь к формуле, выражающей определитель
3-го порядка: Произведем
группировку по элементам первой
строки, вынося затем за скобки
множители
Выражения,
стоящие в скобках представляют собой
миноры элементов-сомножителей: Чтобы
добиться равенства знаков, заметим:
В
итоге получим:
«Определитель равен сумме попарных произведений элементов первой строки на их алгебраические дополнения». Такое представление определителя называется его разложением по элементам первой строки. Аналогично можно было группировать слагаемые по элементам любой другой строки или столбца. Т.е., для определителя 3-го порядка существует 6 способов разложений (у него 6 рядов) по элементам ряда.
Например,
вычислим определитель: Раскрываем
его по элементам первой строки
Тут
Тогда
Для определителя произвольного порядка данное правило было обобщено Лапласом и называется теперь правилом Лапласа или правилом разложения определителя по элементам ряда. Его формулировка: «Определитель равен сумме попарных произведений элементов какого-либо ряда на их алгебраические дополнения». По данному правилу следует сделать несколько замечаний:
Так
как в предыдущем примере
Например,
в
Вычислим
Так как первый столбец уже содержит один нуль и в нем есть минус единица, получим на месте тройки тоже нуль. Для этого каждый элемент третьей строки умножим на три и прибавим к соответствующим элементам первой строки. При этом меняется первая строка («к» которой прибавляем), а третья остается без изменений. Получаем:
Теперь,
когда нами получены правила вычисления
определителей, рассмотрим примеры
решения СЛАУ
Например,
решим систему Теперь
определяем
Вычисляем
Находим
После
этого вычисляем
Проверка
|
| |
|
|
| |
Обобщим
формулы Крамера для системы
 линейных уравнений с
линейных уравнений с неизвестными.
неизвестными.
Пусть дана система

Ее основной определитель


Теорема Крамера:
Если
основной определитель системы
 линейных уравнений с
линейных уравнений с неизвестными
отличен от нуля, то эта система имеет
единственное решение, которое можно
найти по формулам:
неизвестными
отличен от нуля, то эта система имеет
единственное решение, которое можно
найти по формулам:
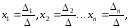
где
 - определитель, полученный из основного
определителя
- определитель, полученный из основного
определителя заменой
заменой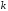 -го
столбца свободными членами системы.
-го
столбца свободными членами системы.

 и
и .
Последуем рассуждениям великих ученых.
.
Последуем рассуждениям великих ученых.
 ,
обращающая оба уравнения системы в
тождество.
,
обращающая оба уравнения системы в
тождество. (исключения
(исключения )
из данной системы уравнений умножим
первое уравнение системы на
)
из данной системы уравнений умножим
первое уравнение системы на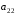 ,
а второе на
,
а второе на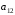 ,
получим:
,
получим: .
. ,
, .
. ,
получаем:
,
получаем:
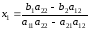 .
. (умножая 1-е уравнение системы на
(умножая 1-е уравнение системы на ,
а 2-е на
,
а 2-е на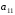 и вычитая из второго первое), получим:
и вычитая из второго первое), получим:
 .
. и
и
 действительно
удовлетворяют исходной системе,
следовательно, являются решением.
действительно
удовлетворяют исходной системе,
следовательно, являются решением. ,
являющееся знаменателем дробей,
определяющих значения неизвестных
,
являющееся знаменателем дробей,
определяющих значения неизвестных
 и
и ,
называетсяопределителем
(детерминантом) 2-го порядка,
обозначается символом
,
называетсяопределителем
(детерминантом) 2-го порядка,
обозначается символом
 или
или (det)
и символически записывается в виде
квадратной таблицы из 4-х чисел,
называемых элементами
определителя:
(det)
и символически записывается в виде
квадратной таблицы из 4-х чисел,
называемых элементами
определителя:
 .
. являются
коэффициентами при неизвестных в
рассматриваемой системе,
являются
коэффициентами при неизвестных в
рассматриваемой системе,
 называетсяосновным
определителем системы.
называетсяосновным
определителем системы. лежат
на главной
диагонали
определителя, а с разными
лежат
на главной
диагонали
определителя, а с разными
 – напобочной
(вспомогательной).
– напобочной
(вспомогательной).


 и
и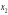 также могут быть представлены в виде
определителей 2-го порядка, которые
мы назовемвспомогательными
и обозначим
также могут быть представлены в виде
определителей 2-го порядка, которые
мы назовемвспомогательными
и обозначим и
и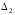 :
: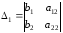 ,
, .
. получается
из основного определителя путем замены
столбца коэффициентов при неизвестной
получается
из основного определителя путем замены
столбца коэффициентов при неизвестной
 столбцом
правых частей. Аналогично составляется
столбцом
правых частей. Аналогично составляется


 неизвестные
обозначают
неизвестные
обозначают
 .
Тогда система совместна
и имеет единственное
решение.
.
Тогда система совместна
и имеет единственное
решение.

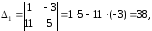


 Проверка:
Проверка:

 Системасовместна
и имеет бесчисленное
множество
решений. Фактически система сводится
к одному уравнению (второе – следствие
первого), из которого неизвестные
однозначно не определяются.
Системасовместна
и имеет бесчисленное
множество
решений. Фактически система сводится
к одному уравнению (второе – следствие
первого), из которого неизвестные
однозначно не определяются.  Здесь
Здесь


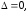 но
но или
или .
Тогда системанесовместна.
.
Тогда системанесовместна.











 :
: .
.
 а
элементы записываются в 3 строки и 3
столбца:
а
элементы записываются в 3 строки и 3
столбца:



 ,
находим
,
находим
 по
формулам Крамера
по
формулам Крамера .
. остается
условием совместности и определенности
СЛАУ, а
остается
условием совместности и определенности
СЛАУ, а показателем
неопределенности либо несовместности
системы в зависимости от значений
показателем
неопределенности либо несовместности
системы в зависимости от значений


 -го)
порядка.
-го)
порядка. -го
порядка (
-го
порядка ( =
1, 2, 3, 4, 5…) и формально записать его в
виде:
=
1, 2, 3, 4, 5…) и формально записать его в
виде:
 !,
при этом в каждом конкретном произведении
сомножители взяты по одному из каждой
строки и столбца, причем каждое
произведение снабжено знаком «+» или
«-» по некоторому правилу.
!,
при этом в каждом конкретном произведении
сомножители взяты по одному из каждой
строки и столбца, причем каждое
произведение снабжено знаком «+» или
«-» по некоторому правилу. в результате последовательного
исключения неизвестных в знаменателях
формул для
в результате последовательного
исключения неизвестных в знаменателях
формул для получается выражение вида:
получается выражение вида:



 -го
порядка. Рассмотрим ее вывод на примере
определителя 3-го порядка. Но для начала
нам небходимо ввести некоторые
дополнительные понятия.
-го
порядка. Рассмотрим ее вывод на примере
определителя 3-го порядка. Но для начала
нам небходимо ввести некоторые
дополнительные понятия. определителя
определителя
 -го
порядка называется определитель,
который получается из данного
вычеркиванием
-го
порядка называется определитель,
который получается из данного
вычеркиванием -й
строки и
-й
строки и
 –го
столбца, на пересечении которых стоит
данный элемент.
–го
столбца, на пересечении которых стоит
данный элемент. обозначается
обозначается
 .
. определителя
называется минор, взятый со своим или
противоположным знаком согласно
правилу: если сумма номеров строки и
столбца, на пересечении которых стоит
элемент, есть число четное, то минор
берется со своим знаком, если же
нечетное, то с противоположным.
Обозначается алгебраическое дополнение
определителя
называется минор, взятый со своим или
противоположным знаком согласно
правилу: если сумма номеров строки и
столбца, на пересечении которых стоит
элемент, есть число четное, то минор
берется со своим знаком, если же
нечетное, то с противоположным.
Обозначается алгебраическое дополнение
 :
:

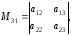


 :
:



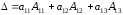 или словами:
или словами: ,
, ,
,
 ,
, ,
,
 .
. .
.

 -го
порядка выражается через
-го
порядка выражается через определителей (
определителей ( -1)-го
порядка. В итоге вычисление определителя
-1)-го
порядка. В итоге вычисление определителя -го порядка может быть сведено к
вычислению
-го порядка может быть сведено к
вычислению
 определителей
2-го порядка.
определителей
2-го порядка.

 разложение выгодно вести либо по
третьему столбцу, либо по третьей
строке.
разложение выгодно вести либо по
третьему столбцу, либо по третьей
строке.
 Далее раскладываем определитель по
элементам первого столбца:
Далее раскладываем определитель по
элементам первого столбца:

 методом Крамера.
методом Крамера. ,
для которой
,
для которой

 ,
путем замены первого столбца столбцом
свободных членов
,
путем замены первого столбца столбцом
свободных членов



