Министерство аграрной политики и продовольствия Украины

Государственное агентство рыбного хозяйства Украины

Керченский государственный морской технологический университет

Кафедра высшей математики и физики

Высшая математика

Конспект лекций

Раздел

Элементы линейной алгебры

для студентов дневной и заочной форм обучения

направления 6.050503 «Машиностроение»

Керчь, 2013 г.

УДК 51

Автор (составитель): Егорова С.Н., старший преподаватель кафедры высшей математики и физики КГМТУ

Рецензент: Кузьменко С.Н., кандидат физико-математических наук, доцент кафедры ВМ и Ф, КГМТУ

Конспект лекций рассмотрен и одобрен на заседании кафедры ВМ и Ф КГМТУ,

протокол № от ____________ 2013 г.

Конспект лекций рассмотрен и одобрен на заседании методической комиссии

технологического факультета КГМТУ,

протокол № ____ от______________ 2013 г.

Керченский государственный морской технологический университет, 2013 г.

Содержание

ВВЕДЕНИЕ………………………………………………………………………….	4
ТЕМАТИЧЕСКИЙ ПЛАН………………………………………………………....	5
1.ЭЛЕМЕНТЫ ЛИНЕЙНОЙ АЛГЕБРЫ………………………………………….	6
1.1 Понятие системы линейных алгебраических уравнений (СЛАУ)…………..	6
1.2 Решение СЛАУ размера 2x2…………………………………………………...	7
1.2.1 Понятие определителя 2-го порядка………………………………………...	7
1.2.2 Формулы Крамера решения СЛАУ………………………………………….	9
1.2.3.Свойства определителя……………………………………………………….	10
1.3 Решение СЛАУ размера 3x3…………………………………………………...	11
1.3.1 Понятие определителя 3-го порядка………………………………………...	11
1.3.2 Понятие определителя произвольного порядка…………………………….	12
1.3.3 Методы вычисления определителя 3-го порядка…………………………...	12
1.3.3.1Правило треугольника………………………………………………………	12
1.3.3.2 Правило Сарруса……………………………………………………………	13
1.3.3.3 Правило Лапласа……………………………………………………………	13
1.4 Матрицы и действия над ними………………………………………………...	19
1.4.1 Понятие матрицы……………………………………………………………..	19
1.4.2 Алгебраические операции над матрицами………………………………….	21
1.5 Матричный способ решения СЛАУ…………………………………………...	25
1.6 Метод Гаусса (метод последовательного исключения неизвестных)………	28
1.7 Исследование систем линейных алгебраических уравнений………………..	33
1.7.1 Понятие ранга матрицы………………………………………………………	34
1.7.2 Теорема Кронеккера-Капелли (о разрешимости СЛАУ)…………………..	36
1.7.3 Исследование однородной СЛАУ…………………………………………...	39
Вопросы для самоконтроля………………………………………………………...	40
Список использованной и рекомендуемой литературы………………………….	41

Введение

Курс высшей математики для технических специальностей традиционно открывается разделом «Элементы линейной алгебры», включающим в себя знакомство с определителями и матрицами и основанные на этих понятиях методы исследования и решения систем линейных алгебраических уравнений.

Линейная алгебра – одна из основных дисциплин, лежащих в основе современной математической науки. Она тесно связана с арифметикой и является обобщением школьного курса алгебры, центральным вопросом которого является решение уравнений.

Решение практических задач алгебраическими методами известно еще со времен древности. Зачатки алгебраических операций просматриваются в вавилонских табличках, египетских папирусах, в «Арифметике» Диофанта.

Появление алгебры как отдельной дисциплины принято связывать с трактатом  средневекового арабского математика Аль-Хорезми«Краткая книга об исчислении аль-джабр и аль-мукабала». Труд Аль-Хорезми учит, как решать уравнения первой и второй степени с числовыми коэффициентами с помощью введенных операций: «аль-джабр» - избавление от членов со знаком «-» в одной части уравнения путем прибавления к обеим частям одинаковых членов и «аль-мукабала» - взаимное исчезновение равных членов в обеих частях уравнения. Трансформировавшись в европейских переводах слово «аль-джабр» превратилось в современную«алгебру».

В 15-17 веках в работах европейских математиков появились применяемые в настоящее время обозначения алгебраических операций («+», «-»), скобки, знаки радикалов, обозначение степеней числа. Франсуа Виетв конце 16 века ввел буквенные обозначения для переменных.

В 17-18 веках под алгеброй понимается наука о вычислениях с использованием переменных, записанных с помощью букв, в частности ставится задача о решении алгебраического уравнения 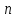- й степени. При решении систем уравнений с одинаковым количеством уравнений и неизвестных в 18 веке возникла теория определителей. Чуть позднее, в начале 19 века была разработана теория матриц, с помощью которой были предложены новые способы исследования систем линейных уравнений.

С середины 19 века в центре алгебраических исследований оказывается изучение произвольных алгебраических операций. Предметом изучения современной алгебры являются множества и пространства различной природы с заданными на них алгебраическими операциями.

Свое обобщение и дальнейшее развитие идеи линейной алгебры находят отражение в последующих разделах вузовской высшей математики, таких как «Элементы векторной алгебры», «Элементы аналитической геометрии».