5. Скорость истечения

Чтобы найти скорость истечения газа через сопло, нужно проинтегрировать уравнение:

; ,

где w ₁ и w ₂ – значения скорости в конце и начале процесса.

Для случаев, когда , w ₂  w ₁, то членом ₁ можно пренебречь, получаем:

, (9.17)

но т.к. l₀ связано с параметрами , можно записать:

,

или

(9.18)

Из последних формул видно, что скорость истечения определяется параметрами газа на входе в сопло и его давлением P₂ на выходе, или разностью энтальпий h₀ на входе и выходе из сопла.

При истечении газа в вакуум (P₂ = 0) скорость истечения будет максимальная.

. (9.19)

6. Секундный расход идеального газа через сопло

Массовый расход газа через сопло определяется по уравнению неразрывности

,

где F₂ – площадь выходного сечения; v₂ – удельный объем. v₂ можно определить из соотношения параметров в адиабатном процессе:

.

Подставляя значения удельного объема v₂ и скорость истечения  в уравнение неразрывности, получаем:

,

или

.

Таким образом, массовый секундный расход газа зависит от площади выходного сечения сопла F₂, параметров газа на входе и степени его расширения.

7. Истечение газа из сосуда неограниченной емкости

Рассмотрим истечение газа из бесконечно большого резервуара (рис. 9.4), в котором параметры газа ; параметры на срезе сопла ; параметры окружающей среды . Начальную скорость в резервуаре принимаем равной нулю (= 0).

Рис. 9.4. Истечение газа из резервуара через суживающееся сопло

Если истечение является обратимым адиабатным, то

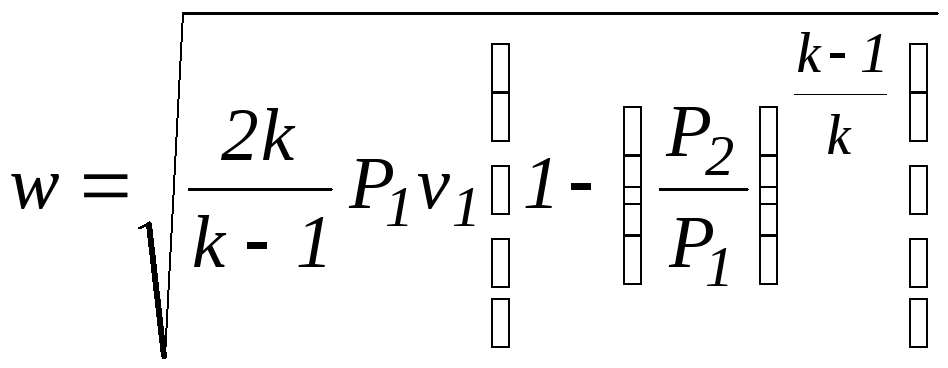
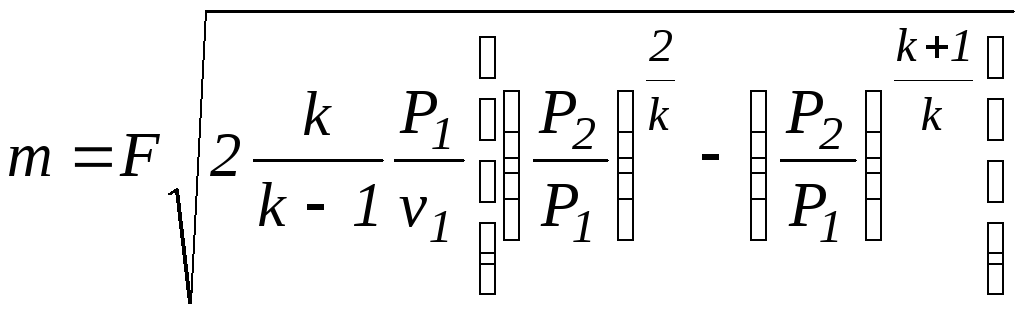
Таким образом, для данного газа и заданных параметров газа и скоростьw и расход газа m зависят только от отношения давления , т.е. от давления во внешнем пространстве, куда истекает газ. Анализ показывает, что при, когда = 1, скорость истечения газа равна нулю, с уменьшением  скорость все время возрастает и при 0, когда = 0 оно достигает максимального значения. Расход газа m становится равным нулю при, когда = 1, и при 0, когда = 0.

Между этими граничными значениями  расход m больше нуля, а при некотором определенном отношении давлений расход газа m и скорость истечения  становятся максимальными. В точке максимума производная расхода m по  превращается в ноль. Давление , при которомm = m_max и w = w _max, называется критическим . Для определения критического отношения давленийвозьмем первую производную от последней зависимости, которая стоит в квадратных скобках под корнем и приравняем ее к нулю.

,

отсюда

(9.20)

Критическое отношение давлений зависит только от показателя адиабаты k, т.е. от физических свойств газа. Для одноатомного газа k = 1,66, _кр = 0,49; для двухатомного: k = 1,41, _кр = 0,528; для трехатомного: k = 1,33, _кр = 0,546. С учетом изложенного можно записать:

, (9.21)

т.е. критическое давление равно начальному давлению, умноженному на коэффициент _кр.

Рис. 9.5. Зависимость расхода газа (а) от скорости истечения (б) и удельного объема (в)

при истечении от отношения давлений

Из рисунка 9.5 видно, что при уменьшении перепада давлений от  = ₁ до  = _кр расход газа m возрастает от m = 0 при  = 1 до m = m_max = m_кр при  = _кр, т.е. на срезе сопла наступает такой режим течения, когда расход газа m, скорость  и удельный объем v достигают своего предельного значения. При дальнейшем понижении давления до   _кр, изменение расхода газа m соответствуют участки кривой bc и bo. Участок bo получен по теоретической зависимости. Действительное же изменение расхода происходит по линии bс.