5. Адиабатный процесс

Адиабатный процесс- это процесс без теплообмена с внешней средой. При адиабатном процессе энергообмен рабочего тела с окружающей средой происходит только в форме работы, энергообмена в форме теплоты нет. Эти условия выражаются соотношением: . Тогда уравнение первого закона термодинамики для адиабатного процесса имеет вид:

. (5.4)

Из этого уравнения видно, что работа адиабатного процесса расширения совершается вследствие уменьшения внутренней энергии газа и, следовательно, температура газа уменьшается. Работа адиабатного сжатия полностью идет на увеличение внутренней энергии газа, то есть на повышение его температуры. Таким образом, изменение внутренней энергии и работа в адиабатном процессе эквивалентны по величине и противоположны по знаку.

Выведем уравнение адиабаты для идеального газа. Воспользуемся уравнением первого закона термодинамики:

т.к. , то

(5.5)

Разделив переменные, получим:

(5.6)

Интегрируя (5.6) при k = const, получим , откуда

(5.7)

Уравнение (5.7) является уравнением адиабаты.

На рис. 5.10 приведен адиабатный процесс расширения газа в -диаграмме.

Из уравнения (5.7) следует:

, (5.8)

то есть при адиабатном расширении давление падает, а при сжатии возрастает.

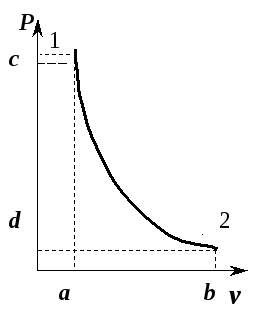
Рис. 5.10. Адиабата идеального газа

Учитывая, что в адиабатном процессе изменяются все три параметра состояния, необходимо выявить зависимости между v и T, p и T.

Зависимость между температурой T и объемом v можно получить из уравнения (5.8) и уравнений состояния, записанных для точек процесса 1 и 2: Р₁v₁ = RT₁ и Р₂v₂=RT₂, откуда

(5.9)

Из уравнений (5.8) и (5.9) следует:

(5.10)

Далее из уравнений (5.8) и (5.10) следует:

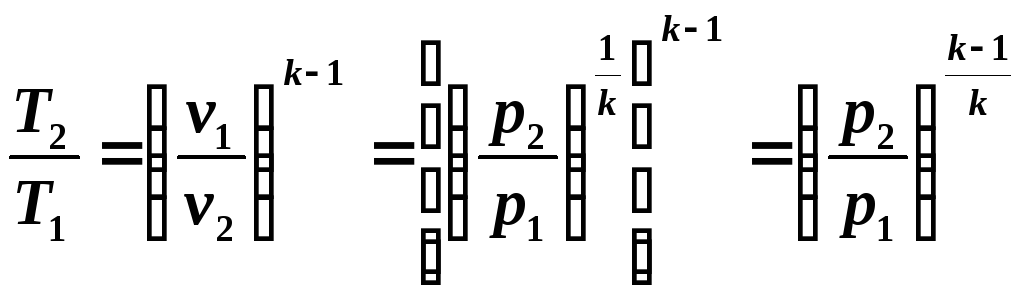
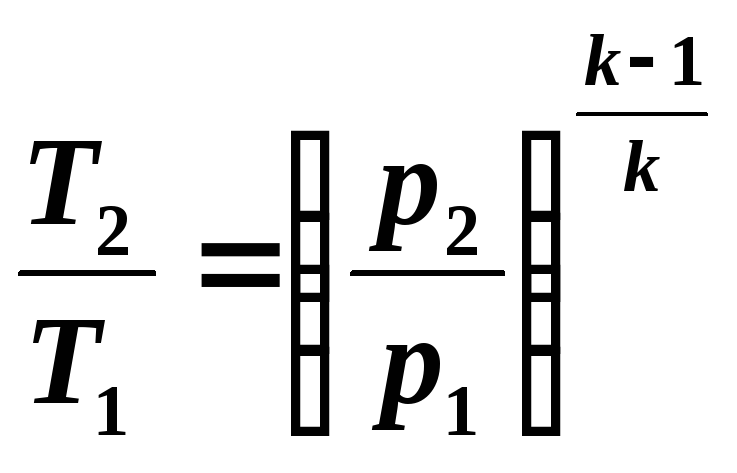(5.11)

При k = const для вычисления работы адиабатного процесса можно записать несколько формул. Из уравнения приc_v = const имеем:

(5.12)

Учитывая соотношения (5.10) и (5.11), уравнение (5.12) запишем в виде:

(5.13)

Располагаемая работа в адиабатном процессе определим из соотношения

, то есть

(5.14)

Для обратимого адиабатного процесса , поэтому

, то есть обратимый адиабатный процесс будет изоэнтропным и в -диаграмме изображается прямой линией, параллельной оси(рис. 5.11). Процесс адиабатного расширения изображается вертикальной прямой 2-1, идущей вниз, а процесс адиабатного сжатия 1-2 – вертикальной прямой, идущей вверх.

Рис. 5.11. Адиабатный процесс в -диаграмме

Теплоемкость в адиабатном процессе равна нулю: .

a

a

Рис. 5.12. Схема распределения энергии в адиабатном процессе:

а- при расширении газа; б – при сжатии газа

6. Политропный процесс

Политропный процесс – любой произвольный процесс изменения состояния рабочего тела, протекающий при постоянной теплоемкости с_x, то есть c = c_x = const. Линия процесса называется политропой.

Из определения политропного процесса следует, что основные термодинамические процессы (изохорный, изобарный, изотермический, адиабатный, если они протекают при постоянной удельной теплоемкости, являются частными случаями политропного процесса.

Другими словами, политропный процесс характеризуется одной и той же долей количества подводимой теплоты, расходуемой на изменение внутренней энергии системы.

Уравнение политропного процесса можно получить из уравнений первого закона термодинамики для идеального газа:

далее имеем:

Разделим первое уравнение на второе

и обозначим

,

тогда

Интегрируя полученное соотношение в пределах от начала до конца процесса, находим:

,

или после потенцирования

получаем уравнение политропного процесса

Поскольку уравнение политропы отличается от уравнения адиабаты только значением показателя n, то все соотношения между основными параметрами могут быть представлены формулами, аналогичными формулам для адиабатного процесса:

Удельная теплоемкость политропного процесса может быть определена из выражения для показателя политропы

, откуда ,

где k – показатель адиабаты.

Последнее уравнение позволяет определить удельную теплоемкость политропного процесса для любого значения n. Если в это уравнение подставить значения для частных случаев, то можно получить:

Изохорный процесс:	n = ;		c = cv;	v = const.
Изобарный процесс:	n = 0;	c = kcv = cp;		p = const.
Изотермический процесс:	n = 1;	c = ;		T = const.
Адиабатный процесс:	n = k;	c = 0;		pvk = const.

Характер зависимости от показателя политропыn графически показан на рис. 5.13.

Рис.5.13. Зависимость теплоемкости от показателя политропы.

Уравнение удельной работы изменения объема, совершаемой телом при политропном процессе, имеет аналогичный вид с уравнением удельной работы в адиабатном процессе

или

.

Располагаемая работа равна:

Изменение удельной внутренней энергии газа и теплота в политропном процессе определяются из уравнений:

.

Изменение удельной энтальпии определяется по формуле, справедливой для всех процессов идеального газа, включая политропный процесс:

.

Изменение удельной энтропии газа в политропном процессе равно:

или для конечного изменения состояния

.

Значение показателя политропы в любом политропном процессе может быть определено по координатам любых двух точек графика:

; ;.

Если в vP- и sT – координатах выбрать некоторую произвольную точку и провести из нее все рассмотренные термодинамические процессы, то все поле построенной таким образом диаграммы делится на восемь областей, характеризующихся определенными признаками (рис. 5.14).

Рис. 5.14. Взаимное расположение политроп в зависимости от величины показателя n