4.2 Анализ электрических цепей при соединении трехфазного источника и приемника по схеме «звезда» с нулевым проводом

У источника энергии, выполненного по схеме «звезда» концы фазных обмоток X, Y, Z генератора соединяются в общий узел в N (рисунок 4.2).

Аналогичный узел n образует соединение концов x, y, z трех фаз приемника, а точки N и n соединяет нейтральный провод, в результате чего потенциалы этих точек равны. Остальные три провода, соединяющие выводы генератора А, В, С с выводами приемника а, в, с называются линейными.

Таким образом, вместо шести проводов (в случае раздельного питания фаз приемника однофазными источниками) трехфазная система, выполненная по схеме «звезда» с нулевым проводом содержит четыре провода.

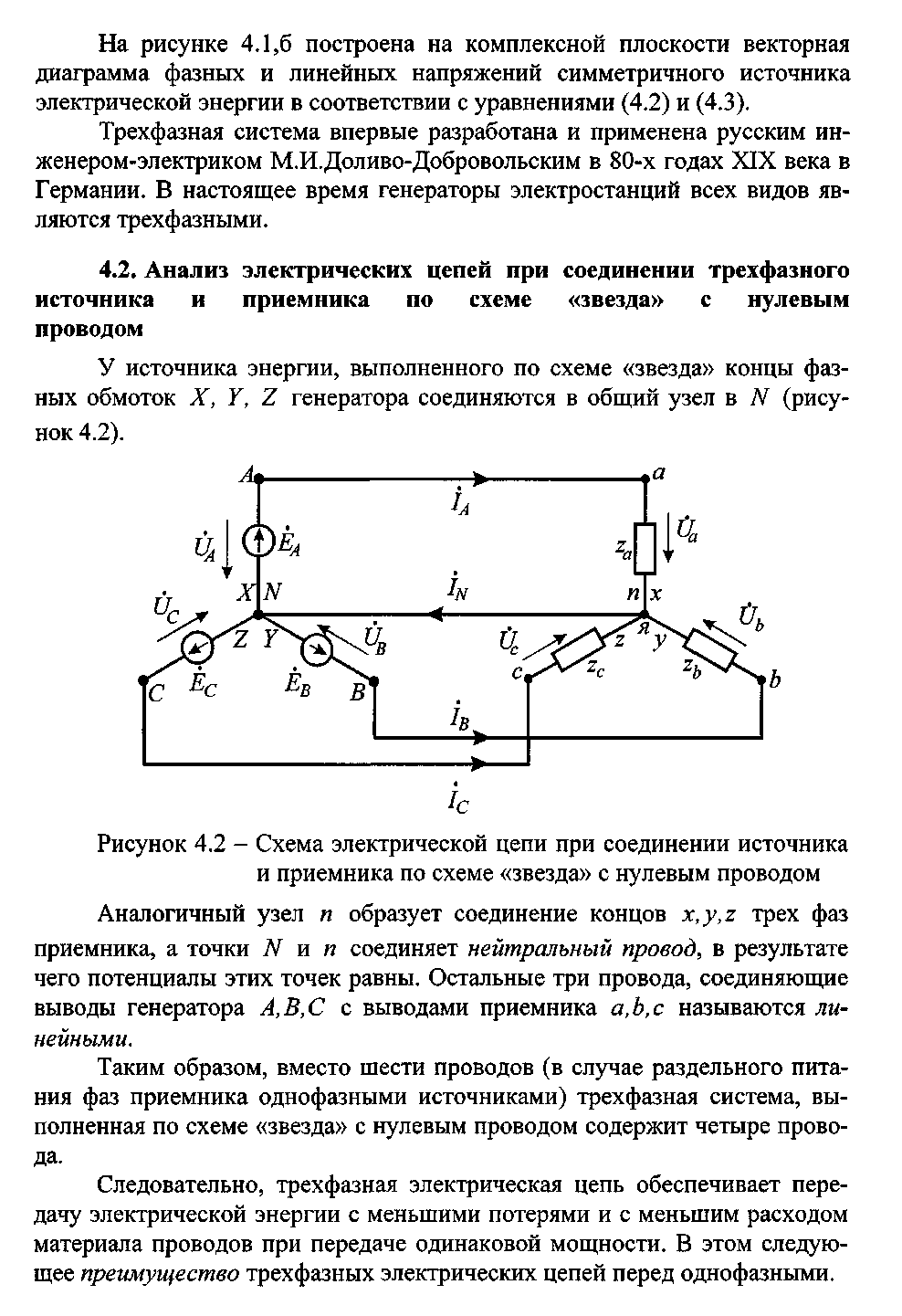
Рисунок 4.2 – Схема электрической цепи при соединении источника и приемника

по схеме «звезда» с нулевым проводом

Следовательно, трехфазная электрическая цепь обеспечивает передачу электрической энергии с меньшими потерями и с меньшим расходом материала проводов при передаче одинаковой мощности. В этом следующее преимущество трехфазных электрических цепей перед однофазными.

Линейные токи в линиях (проводах) A−a, B− b, C−c, определяются по закону Ома в комплексной форме:

(4.4)

Ток в нейтральном проводе связан с линейными токами законом Кирхгофа в комплексной форме: NI&

=+. (4.5)

Очевидно, что в схеме (рисунок 4.2) линейные токи являются одновременно и фазными, т.е. они протекают одновременно в фазах источника и приемника и в соединяющих их проводах (линиях).

Приемник с одинаковыми сопротивлениями всех трех фаз (Z_a=Z_b=Z_c=Z_ф·e^jφ) называется симметричным.

Из уравнений (4.4) следует, что при симметричном приемнике действующие значения линейных токов I_л и токов I_ф всех фаз приемника равны:

I_л = I_ф =I_A=I_B=I_C. (4.6)

Равны также сдвиги фаз φ этих токов относительно соответствующих фазных напряжений.

Таким образом, токи ,представляют симметричную систему токов, в связи с чем их векторная сумма равна нулю и ток в нейтральном проводе согласно (4.5) также равен нулю.

Векторная диаграмма напряжений и токов при емкостном характере симметричного приемника (ток опережает напряжение по фазе на угол φ) изображена на рисунке 4.3,а.

Векторная диаграмма напряжений на рисунке 4.3,а повторяет векторную диаграмму напряжений источника электрической энергии (рисунок 4.1), т.к. система фазных и линейных напряжений в рассматриваемой электрической цепи задается источником и не зависит от нагрузки. В этом достоинство электрической цепи с нулевым проводом.

Составим уравнение по второму закону Кирхгофа для контура ANBA (рисунок 4.2):

(4.7)

где – комплекс линейного напряжения.

Рисунок 4.3 – Векторная диаграмма напряжений и токов трехфазной электрической цепи

при соединении симметричного приемника и источника по схеме «звезда»

при емкостном характере приемника (а), при несимметричном приемнике (б)

На векторной диаграмме вектор направлен в т. A так, чтобы выполнялось условие (4.7).

Физически это направление вектора указывает, что условно потенциал т. A выше потенциала т. В.

Из векторной диаграммы следует, что при симметричном приемнике, соединенном в «звезду», и при наличии нулевого (нейтрального) провода, симметричной системе напряжений (4.3) соответствует симметричная система токов:

(4.8)

Однако, если приемник несимметричный, токи в схеме (рисунок 4.2) не будут представлять симметричную систему и в нулевом проводе в соответствии с (4.5) появится ток .

На рисунке 4.3,б приведена векторная диаграмма токов для случая несимметричного приемника емкостного характера.