3.2 Элементы электрических цепей синусоидального тока

Основные элементы электрических цепей синусоидального тока:

- источники электрической энергии (источники ЭДС и источники тока);

- резистивные элементы (резисторы, реостаты, нагревательные элементы и т.д.);

- емкостные элементы (конденсаторы);

- индуктивные элементы (катушки индуктивности).

3.2.1 Резистивный элемент (рэ)

На рисунке 3.4, а изображен РЭ, по которому течет ток

i= I_т sinωt. (3.18)

По закону Ома напряжение РЭ

u=i·R=R·I_msinωt= U_m sinωt, (3.19)

где U_m=R·I_m.

Из формул (3.18) и (3.19) следует вывод: ток и напряжение в резистивном элементе совпадают по фазе (изменяются синфазно). Это положение наглядно иллюстрируется на рисунке 3.4,б, в.

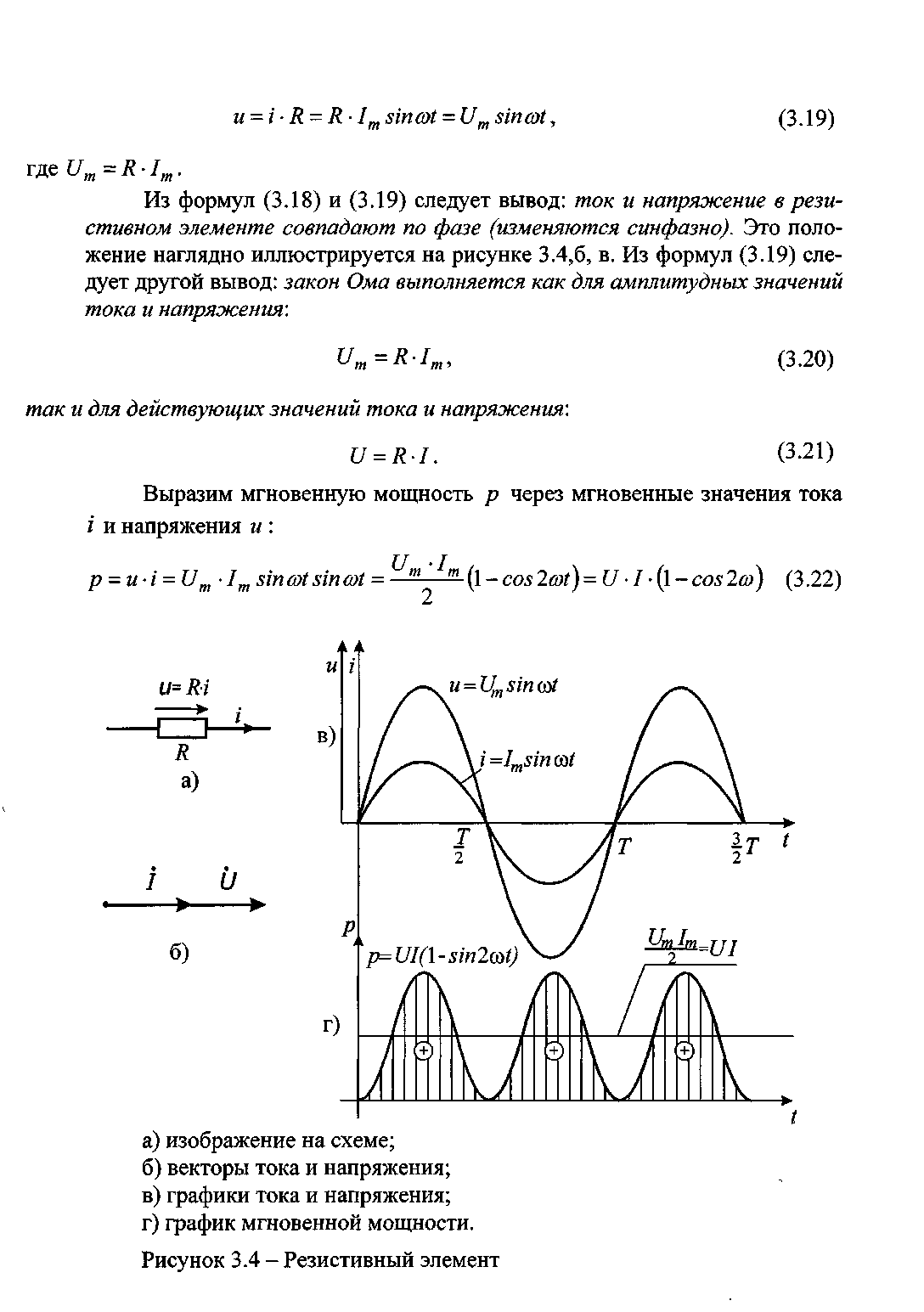
Рисунок 3.4 – Резистивный элемент: а) изображение на схеме; б) векторы тока и напряжения; в) графики тока и напряжения; г) график мгновенной мощности

Из формул (3.19) следует другой вывод: закон Ома выполняется как для амплитудных значений тока и напряжения:

U_m=R·I_m, (3.20)

так и для действующих значений тока и напряжения:

U=R·I. (3.21)

Выразим мгновенную мощность p через мгновенные значения тока i и напряжения u:

p = u·i = U_m I_msinωtsinωt =(3.22)

График изменения мощности p во времени представлен на рисунке 3.4, г. Анализ графика и формулы (3.22) позволяют сделать выводы:

- мгновенная мощность p имеет постоянную составляющую и переменную составляющую, изменяющуюся с частотой 2ω;

- мощность в любой момент времени положительна (р>0). Это значит, что в резистивном элементе происходит необратимое преобразование электрической энергии в другие виды энергии («потребление» энергии);

- постоянная составляющая в формуле (3.22) есть среднее значение мгновенной мощности за промежуток времени равный периоду Т. Следовательно, энергия W, преобразуемая в резистивном элементе в течение периода, подсчитывается по формуле:

. (3.23)

Энергия, преобразуемая в резистивном элементе за любой промежуток времени от 0 до t определяется по формуле

. (3.24)

3.2.2 Индуктивный элемент

Классическим примером индуктивного элемента (ИЭ) является катушка индуктивности – провод, намотанный на изоляционный каркас (рисунок 3.5,а).

На рисунке 3.5,б изображен индуктивный элемент, по которому течет ток

i_L = I_msinωt. (3.25)

Согласно закону электромагнитной индукции напряжение на индуктивном элементе

т.е. (3.26)

где Ф – магнитный поток, сконцентрированный внутри индуктивного эле-мента (катушки индуктивности);

L – индуктивность элемента (коэффициент пропорциональности между магнитным потоком и током в индуктивном элементе), для линейного индуктивного элемента индуктивность L=const.

Подставляя в (3.26) выражение (3.25), получим:

u_L = ω·L·I_mcosωt = U_m sin (ωt+90°), (3.27)

где U_m = ω L·I_m = X_L·I_m.

Величина X_L = ω L называется индуктивным сопротивлением, измеряется в омах и зависит от частоты ω.

Сопоставляя выражения (3.25) и (3.27) сделаем важный вывод: ток в индуктивном элементе отстает по фазе от напряжения на (90°).

Это положение иллюстрируется на рисунке 3.5,в, г. Из формулы (3.27) следует также:

- индуктивный элемент оказывает синусоидальному (переменному) току сопротивление, модуль которого X_L = ω L, прямо пропорционален частоте.

- «Закон Ома» выполняется как для амплитудных значений тока и напряжения:

U_m = X_L·I_m, (3.28)

так и для действующих значений:

U_m = X_L·I_m = X_L·U=X_L·I (3.29)

Выразим мгновенную мощность p через i и u:

p = u·i = U_mcosωt I_msinωt =. (3.30)

График изменения мощности p со временем построен на основании формул (3.30) на рисунке 3.5, д. Анализ графика и (3.30) позволяют сделать выводы:

- мгновенная мощность на индуктивном элементе имеет только переменную составляющую , изменяющуюся с двойной частотой (2ω).

- мощность периодически меняется по знаку: то положительна, то отрицательна. Это значит, что в течение одних четвертьпериодов, когда p > 0, энергия запасается в индуктивном элементе (в виде энергии магнитного поля), а в течение других четвертьпериодов, когда p < 0, энергия возвращается в электрическую цепь.

Рисунок 3.5 – Индуктивный элемент: а) схема конструкции катушки индуктивности;

б) изображение ИЭна схеме; в) векторы тока и напряжения; г) графики тока и напряжения;

д) график мгновенной мощности

Запасаемая в индуктивном элементе энергия за время dt равна:

dW=pdt. (3.31)

Максимальная энергия, запасенная в индуктивном элементе, определится по формуле:

. (3.32)

Подставляя в (3.32) U=I·ω·L, получим:

. (3.33)