
- •Preface
- •Textbook Layout and Design
- •Preliminaries
- •See, Do, Teach
- •Other Conditions for Learning
- •Your Brain and Learning
- •The Method of Three Passes
- •Mathematics
- •Summary
- •Homework for Week 0
- •Summary
- •1.1: Introduction: A Bit of History and Philosophy
- •1.2: Dynamics
- •1.3: Coordinates
- •1.5: Forces
- •1.5.1: The Forces of Nature
- •1.5.2: Force Rules
- •Example 1.6.1: Spring and Mass in Static Force Equilibrium
- •1.7: Simple Motion in One Dimension
- •Example 1.7.1: A Mass Falling from Height H
- •Example 1.7.2: A Constant Force in One Dimension
- •1.7.1: Solving Problems with More Than One Object
- •Example 1.7.4: Braking for Bikes, or Just Breaking Bikes?
- •1.8: Motion in Two Dimensions
- •Example 1.8.1: Trajectory of a Cannonball
- •1.8.2: The Inclined Plane
- •Example 1.8.2: The Inclined Plane
- •1.9: Circular Motion
- •1.9.1: Tangential Velocity
- •1.9.2: Centripetal Acceleration
- •Example 1.9.1: Ball on a String
- •Example 1.9.2: Tether Ball/Conic Pendulum
- •1.9.3: Tangential Acceleration
- •Homework for Week 1
- •Summary
- •2.1: Friction
- •Example 2.1.1: Inclined Plane of Length L with Friction
- •Example 2.1.3: Find The Minimum No-Skid Braking Distance for a Car
- •Example 2.1.4: Car Rounding a Banked Curve with Friction
- •2.2: Drag Forces
- •2.2.1: Stokes, or Laminar Drag
- •2.2.2: Rayleigh, or Turbulent Drag
- •2.2.3: Terminal velocity
- •Example 2.2.1: Falling From a Plane and Surviving
- •2.2.4: Advanced: Solution to Equations of Motion for Turbulent Drag
- •Example 2.2.3: Dropping the Ram
- •2.3.1: Time
- •2.3.2: Space
- •2.4.1: Identifying Inertial Frames
- •Example 2.4.1: Weight in an Elevator
- •Example 2.4.2: Pendulum in a Boxcar
- •2.4.2: Advanced: General Relativity and Accelerating Frames
- •2.5: Just For Fun: Hurricanes
- •Homework for Week 2
- •Week 3: Work and Energy
- •Summary
- •3.1: Work and Kinetic Energy
- •3.1.1: Units of Work and Energy
- •3.1.2: Kinetic Energy
- •3.2: The Work-Kinetic Energy Theorem
- •3.2.1: Derivation I: Rectangle Approximation Summation
- •3.2.2: Derivation II: Calculus-y (Chain Rule) Derivation
- •Example 3.2.1: Pulling a Block
- •Example 3.2.2: Range of a Spring Gun
- •3.3: Conservative Forces: Potential Energy
- •3.3.1: Force from Potential Energy
- •3.3.2: Potential Energy Function for Near-Earth Gravity
- •3.3.3: Springs
- •3.4: Conservation of Mechanical Energy
- •3.4.1: Force, Potential Energy, and Total Mechanical Energy
- •Example 3.4.1: Falling Ball Reprise
- •Example 3.4.2: Block Sliding Down Frictionless Incline Reprise
- •Example 3.4.3: A Simple Pendulum
- •Example 3.4.4: Looping the Loop
- •3.5: Generalized Work-Mechanical Energy Theorem
- •Example 3.5.1: Block Sliding Down a Rough Incline
- •Example 3.5.2: A Spring and Rough Incline
- •3.5.1: Heat and Conservation of Energy
- •3.6: Power
- •Example 3.6.1: Rocket Power
- •3.7: Equilibrium
- •3.7.1: Energy Diagrams: Turning Points and Forbidden Regions
- •Homework for Week 3
- •Summary
- •4.1: Systems of Particles
- •Example 4.1.1: Center of Mass of a Few Discrete Particles
- •4.1.2: Coarse Graining: Continuous Mass Distributions
- •Example 4.1.2: Center of Mass of a Continuous Rod
- •Example 4.1.3: Center of mass of a circular wedge
- •4.2: Momentum
- •4.2.1: The Law of Conservation of Momentum
- •4.3: Impulse
- •Example 4.3.1: Average Force Driving a Golf Ball
- •Example 4.3.2: Force, Impulse and Momentum for Windshield and Bug
- •4.3.1: The Impulse Approximation
- •4.3.2: Impulse, Fluids, and Pressure
- •4.4: Center of Mass Reference Frame
- •4.5: Collisions
- •4.5.1: Momentum Conservation in the Impulse Approximation
- •4.5.2: Elastic Collisions
- •4.5.3: Fully Inelastic Collisions
- •4.5.4: Partially Inelastic Collisions
- •4.6: 1-D Elastic Collisions
- •4.6.1: The Relative Velocity Approach
- •4.6.2: 1D Elastic Collision in the Center of Mass Frame
- •4.7: Elastic Collisions in 2-3 Dimensions
- •4.8: Inelastic Collisions
- •Example 4.8.1: One-dimensional Fully Inelastic Collision (only)
- •Example 4.8.2: Ballistic Pendulum
- •Example 4.8.3: Partially Inelastic Collision
- •4.9: Kinetic Energy in the CM Frame
- •Homework for Week 4
- •Summary
- •5.1: Rotational Coordinates in One Dimension
- •5.2.1: The r-dependence of Torque
- •5.2.2: Summing the Moment of Inertia
- •5.3: The Moment of Inertia
- •Example 5.3.1: The Moment of Inertia of a Rod Pivoted at One End
- •5.3.1: Moment of Inertia of a General Rigid Body
- •Example 5.3.2: Moment of Inertia of a Ring
- •Example 5.3.3: Moment of Inertia of a Disk
- •5.3.2: Table of Useful Moments of Inertia
- •5.4: Torque as a Cross Product
- •Example 5.4.1: Rolling the Spool
- •5.5: Torque and the Center of Gravity
- •Example 5.5.1: The Angular Acceleration of a Hanging Rod
- •Example 5.6.1: A Disk Rolling Down an Incline
- •5.7: Rotational Work and Energy
- •5.7.1: Work Done on a Rigid Object
- •5.7.2: The Rolling Constraint and Work
- •Example 5.7.2: Unrolling Spool
- •Example 5.7.3: A Rolling Ball Loops-the-Loop
- •5.8: The Parallel Axis Theorem
- •Example 5.8.1: Moon Around Earth, Earth Around Sun
- •Example 5.8.2: Moment of Inertia of a Hoop Pivoted on One Side
- •5.9: Perpendicular Axis Theorem
- •Example 5.9.1: Moment of Inertia of Hoop for Planar Axis
- •Homework for Week 5
- •Summary
- •6.1: Vector Torque
- •6.2: Total Torque
- •6.2.1: The Law of Conservation of Angular Momentum
- •Example 6.3.1: Angular Momentum of a Point Mass Moving in a Circle
- •Example 6.3.2: Angular Momentum of a Rod Swinging in a Circle
- •Example 6.3.3: Angular Momentum of a Rotating Disk
- •Example 6.3.4: Angular Momentum of Rod Sweeping out Cone
- •6.4: Angular Momentum Conservation
- •Example 6.4.1: The Spinning Professor
- •6.4.1: Radial Forces and Angular Momentum Conservation
- •Example 6.4.2: Mass Orbits On a String
- •6.5: Collisions
- •Example 6.5.1: Fully Inelastic Collision of Ball of Putty with a Free Rod
- •Example 6.5.2: Fully Inelastic Collision of Ball of Putty with Pivoted Rod
- •6.5.1: More General Collisions
- •Example 6.6.1: Rotating Your Tires
- •6.7: Precession of a Top
- •Homework for Week 6
- •Week 7: Statics
- •Statics Summary
- •7.1: Conditions for Static Equilibrium
- •7.2: Static Equilibrium Problems
- •Example 7.2.1: Balancing a See-Saw
- •Example 7.2.2: Two Saw Horses
- •Example 7.2.3: Hanging a Tavern Sign
- •7.2.1: Equilibrium with a Vector Torque
- •Example 7.2.4: Building a Deck
- •7.3: Tipping
- •Example 7.3.1: Tipping Versus Slipping
- •Example 7.3.2: Tipping While Pushing
- •7.4: Force Couples
- •Example 7.4.1: Rolling the Cylinder Over a Step
- •Homework for Week 7
- •Week 8: Fluids
- •Fluids Summary
- •8.1: General Fluid Properties
- •8.1.1: Pressure
- •8.1.2: Density
- •8.1.3: Compressibility
- •8.1.5: Properties Summary
- •Static Fluids
- •8.1.8: Variation of Pressure in Incompressible Fluids
- •Example 8.1.1: Barometers
- •Example 8.1.2: Variation of Oceanic Pressure with Depth
- •8.1.9: Variation of Pressure in Compressible Fluids
- •Example 8.1.3: Variation of Atmospheric Pressure with Height
- •Example 8.2.1: A Hydraulic Lift
- •8.3: Fluid Displacement and Buoyancy
- •Example 8.3.1: Testing the Crown I
- •Example 8.3.2: Testing the Crown II
- •8.4: Fluid Flow
- •8.4.1: Conservation of Flow
- •Example 8.4.1: Emptying the Iced Tea
- •8.4.3: Fluid Viscosity and Resistance
- •8.4.4: A Brief Note on Turbulence
- •8.5: The Human Circulatory System
- •Example 8.5.1: Atherosclerotic Plaque Partially Occludes a Blood Vessel
- •Example 8.5.2: Aneurisms
- •Homework for Week 8
- •Week 9: Oscillations
- •Oscillation Summary
- •9.1: The Simple Harmonic Oscillator
- •9.1.1: The Archetypical Simple Harmonic Oscillator: A Mass on a Spring
- •9.1.2: The Simple Harmonic Oscillator Solution
- •9.1.3: Plotting the Solution: Relations Involving
- •9.1.4: The Energy of a Mass on a Spring
- •9.2: The Pendulum
- •9.2.1: The Physical Pendulum
- •9.3: Damped Oscillation
- •9.3.1: Properties of the Damped Oscillator
- •Example 9.3.1: Car Shock Absorbers
- •9.4: Damped, Driven Oscillation: Resonance
- •9.4.1: Harmonic Driving Forces
- •9.4.2: Solution to Damped, Driven, Simple Harmonic Oscillator
- •9.5: Elastic Properties of Materials
- •9.5.1: Simple Models for Molecular Bonds
- •9.5.2: The Force Constant
- •9.5.3: A Microscopic Picture of a Solid
- •9.5.4: Shear Forces and the Shear Modulus
- •9.5.5: Deformation and Fracture
- •9.6: Human Bone
- •Example 9.6.1: Scaling of Bones with Animal Size
- •Homework for Week 9
- •Week 10: The Wave Equation
- •Wave Summary
- •10.1: Waves
- •10.2: Waves on a String
- •10.3: Solutions to the Wave Equation
- •10.3.1: An Important Property of Waves: Superposition
- •10.3.2: Arbitrary Waveforms Propagating to the Left or Right
- •10.3.3: Harmonic Waveforms Propagating to the Left or Right
- •10.3.4: Stationary Waves
- •10.5: Energy
- •Homework for Week 10
- •Week 11: Sound
- •Sound Summary
- •11.1: Sound Waves in a Fluid
- •11.2: Sound Wave Solutions
- •11.3: Sound Wave Intensity
- •11.3.1: Sound Displacement and Intensity In Terms of Pressure
- •11.3.2: Sound Pressure and Decibels
- •11.4: Doppler Shift
- •11.4.1: Moving Source
- •11.4.2: Moving Receiver
- •11.4.3: Moving Source and Moving Receiver
- •11.5: Standing Waves in Pipes
- •11.5.1: Pipe Closed at Both Ends
- •11.5.2: Pipe Closed at One End
- •11.5.3: Pipe Open at Both Ends
- •11.6: Beats
- •11.7: Interference and Sound Waves
- •Homework for Week 11
- •Week 12: Gravity
- •Gravity Summary
- •12.1: Cosmological Models
- •12.2.1: Ellipses and Conic Sections
- •12.4: The Gravitational Field
- •12.4.1: Spheres, Shells, General Mass Distributions
- •12.5: Gravitational Potential Energy
- •12.6: Energy Diagrams and Orbits
- •12.7: Escape Velocity, Escape Energy
- •Example 12.7.1: How to Cause an Extinction Event
- •Homework for Week 12
Week 6: Vector Torque and Angular Momentum |
305 |
Homework for Week 6
Problem 1.
Physics Concepts: Make this week’s physics concepts summary as you work all of the problems in this week’s assignment. Be sure to cross-reference each concept in the summary to the problem(s) they were key to, and include concepts from previous weeks as necessary. Do the work carefully enough that you can (after it has been handed in and graded) punch it and add it to a three ring binder for review and study come finals!
Problem 2.
ω f
M
R |
v |
m
This problem will help you learn required concepts such as:
•Angular Momentum Conservation
•Inelastic Collisions
so please review them before you begin.
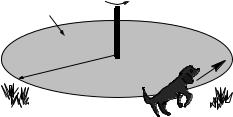
Satchmo, a dog with mass m runs and jumps onto the edge of a merry-go-round (that is initially at rest) and then sits down there to take a ride as it spins. The merry-go-round can be thought of as a disk of radius R and mass M , and has approximately frictionless bearings in its axle. At the time of this angular “collision” Satchmo is travelling at speed v perpendicular to the radius of the merry-go-round and you can neglect Satchmo’s moment of inertia about an axis through his OWN center of mass compared to that of Satchmo travelling around the merry-go-round axis (because R of the merry-go-round is much larger than Satchmo’s size, so we can treat him like “a particle”).
a)What is the angular velocity ωf of the merry-go-round (and Satchmo) right after the collision?
b)How much of Satchmo’s initial kinetic energy was lost, compared to the final kinetic energy of Satchmo plus the merry-go-round, in the collision? (Believe me, no matter what he’s lost it isn’t enough – he’s a border collie and he has plenty more!)
306 |
Week 6: Vector Torque and Angular Momentum |
Problem 3.
ωp
M.R |
ω |
θ |
D |
This problem will help you learn required concepts such as:
•Vector Torque
•Vector Angular Momentum
•Geometry of Precession
so please review them before you begin.
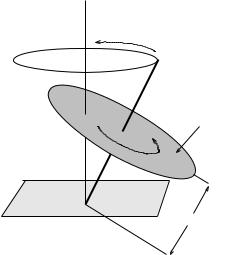
A top is made of a disk of radius R and mass M with a very thin, light nail (r R and m M ) for a spindle so that the disk is a distance D from the tip. The top is spun with a large angular velocity ω. When the top is spinning at a small angle θ with the vertical (as shown) what is the angular frequency ωp of the top’s precession? Note that this is a required problem that will be on at least one test in one form or another, so be sure that you have mastered it when you are done with the homework!
Week 6: Vector Torque and Angular Momentum |
307 |
Problem 4.
d
L
m
v
M
This problem will help you learn required concepts such as:
•Angular Momentum Conservation
•Momentum Conservation
•Inelastic Collisions
•Impulse
so please review them before you begin. You may also find it useful to read: Wikipedia: http://www.wikipedia
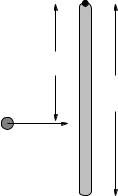
A rod of mass M and length L rests on a frictionless table and is pivoted on a frictionless nail at one end as shown. A blob of putty of mass m approaches with velocity v from the left and strikes the rod a distance d from the end as shown, sticking to the rod.
•Find the angular velocity ω of the system about the nail after the collision.
•Is the linear momentum of the rod/blob system conserved in this collision for a general value of d? If not, why not?
•Is there a value of d for which it is conserved? If there were such a value, it would be called the center of percussion for the rod for this sort of collision.
All answers should be in terms of M , m, L, v and d as needed. Note well that you should clearly indicate what physical principles you are using to solve this problem at the beginning of the work.

308 |
Week 6: Vector Torque and Angular Momentum |
Problem 5.
mr
v 
 F
F
This problem will help you learn required concepts such as:
•Torque Due to Radial Forces
•Angular Momentum Conservation
•Centripetal Acceleration
•Work and Kinetic Energy
so please review them before you begin.
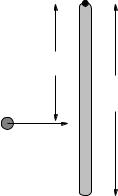
A particle of mass m is tied to a string that passes through a hole in a frictionless table and held. The mass is given a push so that it moves in a circle of radius r at speed v.
a)What is the torque exerted on the particle by the string?
b)What is the magnitude of the angular momentum L of the particle in the direction of the axis of rotation (as a function of m, r and v)?
c)Show that the magnitude of the force (the tension in the string) that must be exerted to keep the particle moving in a circle is:
L2
F= mr3
d)Show that the kinetic energy of the particle in terms of its angular momentum is:
K =
L2
2mr2
Now, suppose that the radius of the orbit and initial speed are ri and vi, respectively. From under the table, the string is slowly pulled down (so that the puck is always moving in an approximately circular trajectory and the tension in the string remains radial) to where the particle is moving in a circle of radius r2.
e)Find its velocity v2 using angular momentum conservation. This should be very easy.
f)Compute the work done by the force from part c) above and identify the answer as the workkinetic energy theorem.
Week 6: Vector Torque and Angular Momentum |
309 |
Problem 6.
z
vin
m
r
θ
pivot |
y |
x
This problem will help you learn required concepts such as:
• Vector Torque
~
• Non-equivalence of L and Iω~.
so please review them before you begin.
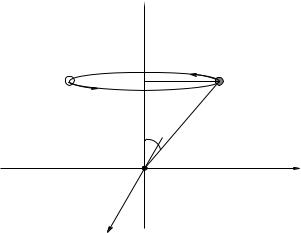
In the figure above, a mass m is being spun in a circular path at a constant speed v around the z-axis on the end of a massless rigid rod of length r pivoted at the orgin (that itself is being pushed by forces not shown). All answers should be given in terms of m, r, θ and v. Ignore gravity and friction.
a)Find the angular momentum vector of this system relative to the pivot at the instant shown and draw it in on a copy of the figure.
b)Find the angular velocity vector of the mass m at the instant shown and draw it in on the
~ |
2 |
sin |
2 |
(θ) is the moment of inertia around the z axis? |
figure above. Is L = Iz ω~, where Iz = mr |
|
|
What component of the angular momentum is equal to Iz ω?
c)What is the magnitude and direction of the torque exerted by the rod on the mass (relative to the pivot shown) in order to keep it moving in this circle at constant speed? (Hint: Consider the precession of the angular momentum around the z-axis where the precession frequency is ω, and follow the method presented in the textbook above.)
d)What is the direction of the force exerted by the rod in order to create this torque? (Hint: Shift gears and think about the actual trajectory of the particle. What must the direction of the force be?)
e)Set τ = rF or τ = r F and determine the magnitude of this torque. Note that it is equal in magnitude to your answer to c) above and has just the right direction!
310 |
Week 6: Vector Torque and Angular Momentum |
Optional Problems
The following problems are not required or to be handed in, but are provided to give you some extra things to work on or test yourself with.
Optional Problem 7.
d
L
m
v
M
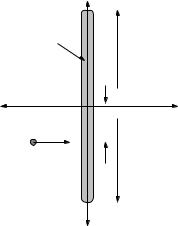
A rod of mass M and length L is hanging vertically from a frictionless pivot (where gravity is “down”). A blob of putty of mass m approaches with velocity v from the left and strikes the rod a distance d from its center of mass as shown, sticking to the rod.
a)Find the angular velocity ωf of the system about the pivot (at the top of the rod) after the collision.
b)Find the distance xcm from the pivot of the center of mass of the rod-putty system immediately after the collision.
c)Find the velocity of the center of mass vcm of the system (immediately) after the collision.
d)Find the kinetic energy of the rod and putty immediately after the collision. Was kinetic energy conserved in this collision? If not, how much energy was lost to heat?
e)After the collision, the rod swings up to a maximum angle θmax and then comes momentarily to rest. Find θmax.
f)In general (for most values of d is linear momentum conserved in this collision? At the risk of giving away the answer, why not? What exerts an external force on the system during the collision when momentum is not conserved?
All answers should be in terms of M , m, L, v, g and d as needed.
Week 7: Statics
Optional Problem 8.
311
M
L
d
v
m
This problem will help you learn required concepts such as:
•Angular Momentum Conservation
•Momentum Conservation
•Inelastic Collisions
•Impulse
so please review them before you begin.
A rod of mass M and length L rests on a frictionless table. A blob of putty of mass m approaches with velocity v from the left and strikes the rod a distance d from the end as shown, sticking to the rod.
•Find the angular velocity ω of the system about the center of mass of the system after the collision. Note that the rod and putty will not be rotating about the center of mass of the rod!
•Is the linear momentum of the rod/blob system conserved in this collision for a general value of d? If not, why not?
•Is kinetic energy conserved in this collision? If not, how much is lost? Where does the energy go?
All answers should be in terms of M , m, L, v and d as needed. Note well that you should clearly indicate what physical principles you are using to solve this problem at the beginning of the work.
312 |
Week 7: Statics |
