[ООП] / Лекции / Lecture_8

Лекция 8

Умножение матриц

Пусть даны матрица А размерностью m×q и матрица B размерностью q×n. Напомним, если число столбцов матрицы А равно числу строк матрицы В, то эти матрицы называются согласованными. Пусть для примера m=3, q=2, n=2, тогда произведение матрицы А на В запишется в виде

С учетом этих обозначений произведение матриц можно представить в виде:

q

где (ai b j ) = ∑aik bkj - скалярное произведение векторов.

k =1

Идеальный случай для реализации данного алгоритма - если матрица А размещается в памяти по строкам, а матрица В - по столбцам, и в векторной машине аппаратно реализована операция скалярного умножения векторов.

При реализации на обычной последовательной машине код на языке С может быть та-

ким:

Такая реализация произведения матриц называется методом внутренних произведений. Последовательность вычисления произведений компонентов векторов для нашего примера условно можно изобразить так:

Существует аналогичный этому метод: двойственный метод внутренних произведений.

Для него в алгоритме (1а) переставим местами циклы по i и j, т.е.

2

А последовательность вычисления произведений компонентов векторов будет такой:

Рассмотрим другой алгоритм, который называется методом средних произведений. Введем обозначения:

a1 =[a11, a21, a31]T , a2 =[a12 , a22 , a32 ]T , b1 =[b11,b21]T , b21 =[b12 ,b22 ]T .

Для последовательной машины алгоритм средних произведений выглядит так:

for(j=0;j<n;j++)

for(k=0;k<q;k++)

for(i=0;i<m;i++) с[i][j]=c[i][j]+a[i][k]*b[k][j];

Последовательность вычисления произведений компонентов векторов будет следующей:

Этот алгоритм удобен при хранении матрицы А по столбцам.

Существует и его двойственный алгоритм средних произведений. Обозначим строки матриц А и В следующим образом:

a1 =[a11, a21] , a2 =[a21, a22 ] , a3 =[a31, a32 ] ; b1 =[b11,b12 ] , b2 =[b21,b22 ] .

Тогда:

Высокопроизводительные вычислительные системы и параллельное программирование. Кудерметов Р.К.

3

Для последовательной машины этот алгоритм запишется в виде:

for(i=0;i<m;i++)

for(k=0;k<n;k++)

for(j=0;j<q;j++)

c[i][j]=c[i][j]+a[i][k]b[k][j];

Последовательность вычисления произведений:

Этот алгоритм эффективен, когда матрица В хранится по строкам.

Далее рассмотрим ещё одну модификацию алгоритма умножения матриц, который на-

зывается алгоритмом внешних произведений:

for(k=0;k<q;k++)

for(j=0;j<n;j++)

for(i=0;i<m;i++)

c[i][j]=c[i][j]+a[i][k]*b[k][j];

Последовательность вычислений:

Очевидно, этот способ выгоден при хранении матрицы А по столбцам, а порядок хранения В не существенен.

И, наконец, двойственный алгоритм внешних произведений:

for(k=0;k<q;k++)

for(i=0;i<m;i++)

for(j=0;j<n;j++)

c[i][j]=c[i][j]+a[i][k]*b[k][j];

Высокопроизводительные вычислительные системы и параллельное программирование. Кудерметов Р.К.

4

Этот алгоритм эффективен, если матрица В хранится по строкам.

Таким образом, мы рассмотрели шесть возможных алгоритмов умножения матриц. Эффективность каждого из них будет определяться типом векторных или параллельных компьютеров, реализацией компиляторов, размером матриц.

Рассмотрим более подробно возможные организации умножения матриц на параллельных вычислительных системах. Не теряя общности предположим что матрицы, которые необходимо умножить – квадратные. Гипотетический случай, когда число процессоров равно числу элементов матрицы легко себе представить. Введем следующие обозначения для строк матрицы A и столбцов матрицы B:

a0 =[a0,0,a0,1,...], a1 =[a1,0,a1,1,...], ...; b0 =[b0,0,b0,1,...]T , b1 =[b0,1,b1,1,...]T ,...,

Тогда можно построить распределение вычислений между процессорами, при котором каждый процессор умножает скалярно строку матрицы A на столбец матрицы B (рис.8.1). В каждом процессоре, таким образом, вычисляется один элемент результирующей матрицы C.

Предположим, что число процессоров равно, числу строк матрицы A, тогда, расположив в каждом процессоре по строке этой матрицы и полностью матрицу B, получим вариант когда в каждом процессоре вычисляется одна строка результирующей матрицы C (рис.8.2).

Аналогично можно построить схему, при которой число процессоров равно числу столбцов матрицы B (рис.8.3). В этом случае в каждом процессоре должна быть расположена вся матрица A и вычисляется один столбец матрицы C.

Если число процессоров меньше, чем число строк матрицы, то общее число строк разделить на равные части по числу процессоров, тогда в каждом процессоре будет вычисляться несколько строк матрицы C. (рис.8.4). Аналогично можно представить схему, при которой столбцы матрицы B равномерно распределяются между процессорами, число которых меньше числа столбцов.

Высокопроизводительные вычислительные системы и параллельное программирование. Кудерметов Р.К.

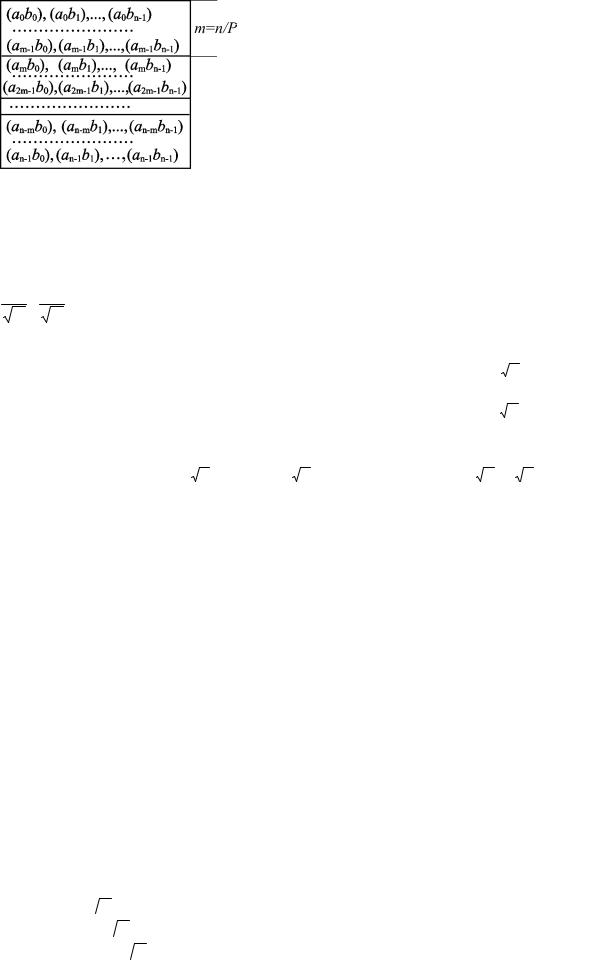
5

Рассмотрим теперь принципиально другой подход к умножению матриц – блочноориентированный. Пусть множество процессоров образуют квадратную двумерную сетку и

или для примера, взяв матрицу размерностью 9 ×9 и число процессоров, равное 9, можем, таким образом разбить матрицы на блоки:

Тогда исходные матрицы A и B запишутся в блочном виде:

Очевидно, что произведение матриц A и B при их блочном представлении можно получить, умножая блоки согласно правилам умножения обычных матриц. Условно, пользуясь С- подобной нотацией, можно записать алгоритм блочного умножения:

for(i=0;i< P ;i++) for(j=0;j< P ;j++)

for(k=0;k< P ;k++)

Высокопроизводительные вычислительные системы и параллельное программирование. Кудерметов Р.К.

6

C[i][j]+=A[i][k]×B[k][j];

где знак умножения × представляет собой подпрограмму умножения обычных матриц, знак суммирования – подпрограмму суммирования матриц, а C[i][j] – блоки матрицы С.

Схему вычисления произведения матриц представим в виде трех подсхем (рис.8.5).

Рис. 8.5

Если три схемы (рис.8.5а, б, с) наложить на матрицу процессоров, которые выполняют умножения подматриц параллельно, то очевидно, что каждый процессор должен содержать соответствующую подматрицу Ai, j и строку подматриц Bi .

Известен алгоритм Канона (Cannon) [ ], для которого затраты памяти равны памяти, необходимой только для хранение трех подматриц (рис.8.6).

Рис. 8.6

Высокопроизводительные вычислительные системы и параллельное программирование. Кудерметов Р.К.