Методичка з ВМ. Статистика
.pdfМІНІСТЕРСТВО ОСВІТИ І НАУКИ УКРАЇНИ
ЗАПОРІЗЬКИЙ НАЦІОНАЛЬНИЙ ТЕХНІЧНИЙ УНІВЕРСИТЕТ
Методичні вказівки та індивідуальні завдання для самостійної роботи
здисципліни
“Математична статистика ”
для студентів економічних спеціальностей (денної форми навчання)
2009
PDF создан испытательной версией pdfFactory Pro www.pdffactory.com
2
Методичні вказівки та індивідуальні завдання для самостійної роботи з дисципліни “Математична статистика” для студентів економічних спеціальностей денної форми навчання / Укл. Коротунова О. В., Щолокова М.О. – Запоріжжя: ЗНТУ, 2009. – 42 с.
Укладачі: |
Коротунова О. В., доцент, к.т.н |
|
Щолокова М.О., доцент, к.т.н |
Експерт: |
Гузь П. В., професор, д.е.н |
Рецензент: |
Мастиновський Ю.В, доцент, к.т.н. |
Відповідальний за випуск: Коротунова О. В., доцент, к.т.н
Затверджено на засіданні кафедри прикладної математики
Протокол № 6 від 27.12.08
Схвалено радою радіоприладобудівного інституту ЗНТУ
Протокол № 5 від 15.01.09
PDF создан испытательной версией pdfFactory Pro www.pdffactory.com
3
ЗМІСТ
1 ТЕОРЕТИЧНІ ВІДОМОСТІ ТА ПРИКЛАДИ РОЗВ’ЯЗАННЯ
ЗАДАЧ |
4 |
|
1.1 |
Первинна обробка вибіркових даних |
4 |
1.2 Точкові та інтервальні оцінки параметрів розподілу |
8 |
|
1.3 |
Перевірка статистичних гіпотез |
10 |
1.3.1 Перевірка гіпотези про математичне сподівання нормально |
||
розподіленої сукупності |
11 |
|
1.3.2 Перевірка гіпотези про рівність дисперсій двох нормально |
|
|
розподілених сукупностей |
12 |
|
1.3.3 Критерій χ 2 Персона |
14 |
|
1.4 |
Елементи теорії кореляції |
15 |
1.5 |
Дисперсійний аналіз |
20 |
2 ІНДИВІДУАЛЬНІ ЗАВДАННЯ |
23 |
|
ЛІТЕРАТУРА |
42 |
|
PDF создан испытательной версией pdfFactory Pro www.pdffactory.com
4
1 ТЕОРЕТИЧНІ ВІДОМОСТІ ТА ПРИКЛАДИ РОЗВ’ЯЗАННЯ ЗАДАЧ
1.1 Первинна обробка вибіркових даних
Генеральною сукупністю в математичній статистиці називається множина однотипних об’єктів, кількісна чи якісна ознака яких підлягає вивченню. Підмножина об’єктів із генеральної сукупності, називається вибірковою сукупністю або вибіркою. Кількість об’єктів n у вибірці називається її об’ємом. Вважаємо, що ознака, яка
вивчається, є випадковою величиною Х із функцією розподілу F(x). Нехай x1 зустрічається у вибірці n1 разів, x2 – n2 , …, xk – nk разів. Числа x1 , x2 , …, xk називаються варіантами, n1 , n2 , …, nk – частотами. Розмістивши числа x1 , x2 , …, xk в порядку зростання і
записавши відповідні частоти, з якими зустрічаються ці значення,
дістанемо варіаційний, або статистичний, ряд:
|
xi |
|
x1 |
|
|
|
x2 |
|
… |
|
xk |
|
|
Частоти |
|
n1 |
|
|
|
n2 |
|
… |
|
nk |
|
|
На підставі такого ряду можна побудувати емпіричну функцію |
|||||||||||
розподілу |
Fn (x)= å |
n(xi ) |
. |
Якщо |
n → ∞ , то емпірична |
функція |
||||||
|
||||||||||||
|
|
|
xi < X |
n |
|
|
|
|
|
|
||
розподілу збігається до теоретичної функції розподілу.
Статистичний ряд графічно подається полігоном частот. Щоб побудувати його, на осі абсцис відкладають значення реалізацій, а на осі ординат – відповідні їм частоти (відносні частоти). Отримані точки сполучають відрізками прямих.
У разі, коли Х – неперервна величина і об’єм вибірки великий, результати вибірки подають інтервальним рядом. Для цього область реалізацій розбивають на k інтервалів і для кожного інтервалу
визначають частоти. Довжину інтервалів hi = xi найчастіше беруть
однаковою ( h ). Отриманий ряд геометрично подається гістограмою. Для побудови її на осі абсцис відкладають інтервали, а на них як на
основах будують прямокутники, висота яких дорівнює ni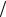 
h (щільність частоти). Гістограма дає певне уявлення про графік
PDF создан испытательной версией pdfFactory Pro www.pdffactory.com
5
щільності розподілу.
Для вибіркової сукупності обчислюють числові характеристики – вибіркові випадкові функції: вибіркову середню x вибіркову
дисперсію |
Dâ |
тощо. Реалізації цих вибіркових функцій знаходять за |
||||||||||||
формулами, вигляд яких залежить від того, в якій формі подано |
||||||||||||||
вибіркові |
дані. |
|
Якщо |
вибіркові |
дані |
не |
згруповано, |
то |
||||||
|
1 |
n |
|
|
1 |
n |
|
|
|
|
|
|
|
|
x = |
åxi , |
Dâ = |
å(xi − x)2 . |
Якщо |
вибіркові |
дані зведено у |
||||||||
|
n i=1 |
|
|
n i=1 |
|
|
|
1 |
k |
|
|
|||
|
|
|
|
|
|
|
|
k |
|
|
|
|||
статистичний |
ряд, то |
x = |
1 å xi ni , |
Dâ = |
å(xi - x)2 ni . |
Для |
||||||||
|
||||||||||||||
практичних |
обчислень |
|
n i=1 |
|
n i=1 |
більш зручно |
||||||||
вибіркової |
дисперсії |
|||||||||||||
використовувати формулу Dâ = x 2 − (x)2 .
Якщо дані подаються інтервальним рядом, то перехід до статистичного ряду виконують, обчислюючи для кожного інтервалу його середину.
Приклад 1.1.1 У цеху встановлено 5 верстатів. Протягом 25 днів реєструвалась кількість верстатів, які не працювали. Здобуто такі значення: 0, 1, 2, 1, 1, 2, 3, 2, 1, 4, 2, 0, 0, 2, 2, 3, 3, 1, 0, 1, 2, 1, 3, 5,
0. Обчислити x , Dâ .
Розв’язання. На підставі вибіркових даних складемо статистичний ряд:
|
xi |
|
|
0 |
|
1 |
2 |
|
3 |
|
4 |
|
5 |
|
|
|
ni |
|
|
5 |
|
7 |
7 |
|
4 |
|
1 |
|
1 |
|
|
|
Знайдемо |
числові |
характеристики вибіркової сукупності. |
|
|
||||||||||
|
k |
|
1 |
|
|
|
|
|
|
|
|
|
|
||
x = 1 å xi ni |
= |
(7 +14 +12 + 4 + 5)= 1,68. |
Вибіркову дисперсію |
||||||||||||
25 |
|||||||||||||||
|
n i=1 |
|
|
|
|
|
|
|
|
|
− (x)2 = : |
||||
визначимо |
|
|
за |
формулою |
|
|
Dâ = x 2 |
||||||||
x 2 = (7 + 28 + 36 +16 + 25)/ 25 = 4,48. Отже, Dâ |
= 4,48 − (1,68)2 |
= 1,6576. |
|||||||||||||
Приклад 1.1.2 За заданим дискретним статистичним розподілом вибірки побудувати емпіричну функцію розподілу та полігон частот:
xi |
–6 |
–4 |
–2 |
2 |
4 |
6 |
Частоти ni |
5 |
10 |
15 |
20 |
40 |
10 |
Розв’язання. Згідно з означенням та властивостями F * (x) має такий
PDF создан испытательной версией pdfFactory Pro www.pdffactory.com
|
|
6 |
|
вигляд (рис. 1.1): |
|
|
|
ì0 |
|
x £ -6, |
|
ï |
0,05 |
- 6 < x £ -4, |
|
ï |
|||
ï |
0,15 |
- 4 < x £ -2, |
|
ï |
|||
F (x) = í |
0,3 |
- 2 |
< x £ 2, |
ï0,5 |
2 |
< x £ 4, |
|
ï |
|
4 |
< x £ 6, |
ï 0,9 |
|||
ï |
1, |
|
x > 6. |
î |
|
||
|
|
|
|
F*(x) |
|
|
|
|
|
|
1 |
|
|
|
|
–6 |
–4 |
–2 |
0 |
2 |
4 |
6 |
хі |
Рисунок 1.1 – Емпірична функція розподілу |
|
||||||
Полігон частот зображено на рис. 1.2. |
|
|
|
|
|||
|
|
|
ni |
|
|
|
|
|
|
|
40 |
|
|
|
|
|
|
|
10 |
|
|
|
|
–6 |
–4 |
–2 |
0 |
2 |
4 |
6 |
xi |
|
|||||||
Рисунок 1.2 – Полігон частот |
|
|
|||||
Приклад 1.1.3 За заданим інтервальним статистичним розподілом вибірки побудувати функцію F * (x) та гістограму частот:
Інтервал |
0-4 |
4-8 |
8-12 |
12-16 |
16-20 |
20-24 |
ni |
5 |
7 |
7 |
4 |
1 |
1 |
PDF создан испытательной версией pdfFactory Pro www.pdffactory.com
|
|
|
|
7 |
|
|
|
Розв’язання. Гістограма зображена на рис. 1.3, а F * (x) – на рис. 1.4. |
|||||||
|
hi |
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
7 |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
0 |
4 |
8 |
12 |
|
16 |
20 |
xi |
|
24 |
||||||
|
Рисунок 1.3 – Гістограма частот |
||||||
|
F (x) |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
0,65 |
|
|
|
|
|
|
|
0,4 |
|
|
|
|
|
|
|
0,1 |
|
|
|
|
|
|
|
0 |
4 |
8 |
12 |
16 |
20 |
24 |
xi |
|
|||||||
Рисунок 1.4 – Емпірична функція розподілу
Приклад 1.1.4 Із генеральної сукупності зроблено вибірку обсягом n=32. Здобуто такі реалізації випадкової величини: 2,2; 7,1; 6,3; 3,9; 5,9; 5,6; 5,6; 4,7; 7,9; 3,2; 6,1; 5,5; 6,4; 6,0; 6,9; 4,7; 6,4; 6,9; 6,7; 7,9; 4,2; 6,7; 6,0; 9,2; 5,5; 6,5; 3,5; 4,9; 7,2; 4,9; 8,9; 5,7. Скласти інтервальний
ряд і знайти x, Dâ .
Розв’язання. Для побудови інтервального ряду розбиваємо область реалізацій на 7 інтервалів з однаковими довжинами інтервалів:
|
max(x )− min(x ) |
|
|
9,2 − |
2,2 |
|
|||
x = |
i |
i |
i |
i |
; |
x = |
=1. Частоти кожного інтервалу |
||
|
|
7 |
|
7 |
|
||||
|
|
|
|
|
|
|
|
||
знайдемо, визначивши для кожного значення інтервал. Якщо значення xi потрапляє на межу, то збільшуємо на 1 частоту нижнього інтервалу.
PDF создан испытательной версией pdfFactory Pro www.pdffactory.com
8
Інтервал 2,2-3,2 3,2-4,2 4,2-5,2 5,2-6,2 6,2-7,2 7,2-8,2 8,2-9,2 |
|||||||
Частота |
2 |
3 |
4 |
9 |
10 |
2 |
2 |
Для обчислення числових характеристик розподілу перейдемо до статистичного ряду. Для цього складемо таблицю, в якій запишемо
середини інтервалів u j = |
x j−1 + x j |
і їхні частоти mj . |
|
|
|
||||||||||||||
2 |
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
u j |
|
2,7 |
|
|
3,7 |
|
4,7 |
|
5,7 |
6,7 |
7,7 |
8,7 |
|
|||||
|
mj |
|
2 |
|
|
|
3 |
|
4 |
|
9 |
10 |
2 |
2 |
|
||||
|
1 |
k |
|
1 |
|
(2,7 ×2 + 3,7 ×3 + 4,7 ×4 + 5,7 ×9 + 6,7 ×10 + 7,7 ×2 + 8,7 ×2) = 5,825 |
|||||||||||||
x = |
å x j m j |
= |
|
||||||||||||||||
n |
|
||||||||||||||||||
|
j=1 |
32 |
|
|
|
|
|
|
|
|
|
|
|
||||||
D = |
1 |
(2,72 ×2+3,72 |
×3+4,72 ×4+5,72 ×9+6,72 ×10+7,72 ×2+8,72 ×2)-(5,825)2 » 2,172 |
||||||||||||||||
|
|||||||||||||||||||
â |
32 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
1.2 Точкові та інтервальні оцінки параметрів розподілу
Оцінка параметра розподілу сукупності θ у загальному випадку є
випадковою величиною, яка визначається за даними вибірки і використовується замість невідомого значення параметра, який потрібно оцінити. Оцінка називається обґрунтованою, якщо вона збігається за ймовірністю до відповідного параметра при n → ∞. Оцінка називається незміщеною, якщо її математичне сподівання збігається зі значенням параметра. У разі вибору з усіх відомих незміщених обґрунтованих оцінок певної оцінки потрібно зазначити критерій, за яким зроблено вибір. Найчастіше застосовується критерій, який полягає у виборі оцінки, що має найменшу можливу дисперсію. Така оцінка називається ефективною.
Нехай маємо точкову оцінку θ параметра θ . Знайдемо для
параметра інтервальну оцінку, скориставшись умовою P(θ) −θ < )= γ. |
|
В такому разі |
називається точністю оцінки, а γ – її надійністю. |
Тоді інтервальна оцінка (довірчий інтервал) для параметра θ набуває вигляду (θ − ;θ + ). Параметр θ – це випадкова величина, надійність
γ можна розглядати як імовірність того, що довірчий інтервал покриває дійсне значення параметра. Величини i γ тісно зв’язані з
об’ємом вибірки n. Якщо задати дві з цих величин, то можна знайти третю. Для цього потрібно знати закон розподілу для
θ = ϕ(X1,X2,...,Xn ).
Нехай ця величина розподілена за нормальним законом. Побудуємо інтервальну оцінку математичного сподівання a = xген за
PDF создан испытательной версией pdfFactory Pro www.pdffactory.com
|
|
|
|
|
9 |
|
|
|
|
|
|
|
||||
значенням вибіркового середнього |
|
в |
для двох випадків: |
|
|
|
||||||||||
x |
|
|
|
|||||||||||||
1. Якщо відомо середнє квадратичне відхилення σ , то довірчий |
||||||||||||||||
інтервал |
для |
|
математичного |
сподівання |
має |
вигляд: |
||||||||||
xB − |
t × |
σ |
|
< a < xB |
+ |
t × |
σ |
|
, де n – об’єм вибірки, |
t – таке значення |
||||||
|
|
|
|
|
|
|||||||||||
n |
|
|||||||||||||||
|
|
|
|
|
n |
|
γ , тобто |
|
|
|
||||||
аргументу функції Лапласа Ф(t) , для якого Ô(t) = |
= t ×σ . |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
n |
|
2. Параметр σ нормального закону розподілу ознаки X генеральної сукупності невідомий. У цьому випадку інтервальна
оцінка параметра a = xген із заданою надійністю γ визначається за
формулою: xв − < a < xв + , де D = tγ × S , S – точкова оцінка
n
параметра σ , виправлене вибіркове середнє квадратичне відхилення tγ = t(γ ,n) – критична точка розподілу Стьюдента, значення якої
можна знайти з таблиць по відомим n і γ .
Для оцінки генерального середнього квадратичного відхилення σ при заданій надійності γ можна побудувати довірчий інтервал s × (1- q) < σ < s × (1+ q), де q = q(n,γ ) – значення, що визначається
таблицями.
Приклад 1.2.1 Знайти довірчий інтервал для математичного сподівання нормально розподіленої випадкової величини, якщо об’єм вибірки n = 49, x В = 2,8 , σ =1,4 , а довірча ймовірність γ = 0,9.
Розв’язання. |
Визначимо |
t , при якому Ф(t) = 0,9 : 2 = 0,45: |
||||||||
t = 1,645 . Тоді 2,8 − |
1,645×1,4 |
< a < 2,8 + |
1,645 |
× |
1,4 |
, або 2,471 < a < 3,129 . |
||||
|
|
|
|
|
|
|
||||
49 |
|
14 |
||||||||
|
|
|
|
|
|
|||||
Приклад 1.2.2 Дана вибірка значень нормально розподіленої випадкової величини: 2, 3, 3, 4, 2, 5, 5, 5, 6, 3, 6, 3, 4, 4, 4, 6, 5, 7, 3, 5.
Знайти с довірчою ймовірністю γ = 0,95 границі довірчих інтервалів
для математичного сподівання та дисперсії.
Розв’язання. Об’єм вибірки n = 20 . Знайдемо x В = 4,25 , S = 1,37 . За таблицями визначимо t(0,95; 20) = 2,093 ; q(0,95; 20) = 0,37 . Тоді
PDF создан испытательной версией pdfFactory Pro www.pdffactory.com
10
4,25 - |
2,093×1,37 |
< a < 4,25 + |
2,093 |
×1,37 , 3,64 < a < 4,86 – довірчий інтервал |
||||
|
|
20 |
|
|
|
20 |
|
|
для |
математичного |
сподівання; |
1,37(1−0,37) <σ <1,37(1+0,37) ; |
|||||
0,86 < σ <1,88; 0,74 < D = σ 2 < 3,52 – довірчий інтервал для дисперсії.
1.3 Перевірка статистичних гіпотез
Статистичною називається гіпотеза, яка стосується виду або параметрів розподілу випадкової величини і яку можна перевірити на підставі результатів спостереження у випадковій вибірці. Перевіряючи статистичні гіпотези за результатами випадкової вибірки, завжди ризикують прийняти хибне рішення. Але в такому випадку можна обчислити ймовірність прийняття хибного рішення і, якщо вона мала, ризик помилки буде невеликим. Помилки, яких можна припуститися, бувають двох родів. Помилка першого роду полягає в тому, що перевірювана гіпотеза H0 відхиляється, тоді як вона правильна.
Помилка другого роду полягає у тому, що гіпотеза H0 приймається, тоді як вона хибна, а правильною є деяка гіпотеза H1. Ця гіпотеза, яка протиставляється гіпотезі H0 , називається альтернативною.
Статистичні гіпотези поділяються на прості і складні. Проста гіпотеза однозначно визначає закон розподілу випадкової величини. Для побудови статистичного критерію, який дає змогу перевірити деяку гіпотезу H0 , необхідно вибрати статистичну характеристику
гіпотези – деяку вибіркову функцію, визначити допустиму ймовірність помилки першого роду α (рівень значущості), сформулювати альтернативну гіпотезу H1, знайти критичну область для статистичної характеристики, щоб мінімізувати ймовірність помилки другого роду. В критичній області гіпотеза H0 відхиляється на користь гіпотези H1. Критична область визначається так, щоб імовірність потрапляння в неї статистичної характеристики за умови, що правильна гіпотеза H0 , дорівнювала α – заданому рівню
значущості. Крім того, необхідно, щоб ймовірність помилки другого роду була мінімальною.
Статистичні гіпотези поділяються на параметричні і
PDF создан испытательной версией pdfFactory Pro www.pdffactory.com