
1305
.pdf
11
А.3 Початкові дані до розрахунку зубчастих зачеплень
А.3.1 Зовнішнє зачеплення
α = 25 |
0 ;h = 1.0;h = 1.0; ρ = 0.35208;С = С = 0.20328; |
|||||||||||
|
|
|
a |
|
f |
a |
|
|
а |
f |
|
|
Таблиця А. 3 -Значення коефіцієнтів зміщень X1, X2 |
|
|||||||||||
Z1 |
Z2 |
|
20 |
25 |
|
31 |
34 |
42 |
50 |
65 |
100 |
150 |
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
20 |
= -0,5 0,5 |
|
= 0 0,5 |
|
|
|
|
|
=0 1,0 |
|
=0 1,5 |
=0 1,5 |
|
1 |
|
2 |
|
|
|
|
|
2 |
|
2 |
2 |
|
X |
|
X |
|
|
|
|
|
X |
|
X |
X |
|
|
|
|
|
|
|
|
|
|
|
|
|
25 |
= 0 0,5 |
|
|
=0 0,5 |
|
|
|
|
=0 1,2 |
|
=0 1,4 |
=0 1,8 |
1 |
|
|
|
|
|
|
|
|||||
|
X |
|
|
X |
|
|
|
|
X |
|
X |
X |
|
|
|
|
2 |
|
|
|
|
2 |
|
2 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
31 |
= -0,5 1,0 |
|
|
|
|
= 0 0,5 |
|
|
=0 1,0 |
|
=0 1,0 |
=0 1,3 |
|
1 |
|
|
|
|
2 |
|
|
2 |
|
2 |
2 |
|
X |
|
|
|
|
X |
|
|
X |
|
X |
X |
|
|
|
|
|
|
|
|
|
|
|
|
|
34 |
= -0,5 1,0 |
|
|
|
|
|
= 0 0,6 |
|
|
=0 1,0 |
=0 1,3 |
=0 1,3 |
|
1 |
|
|
|
|
|
2 |
|
|
2 |
2 |
2 |
|
X |
|
|
|
|
|
X |
|
|
X |
X |
X |
|
|
|
|
|
|
|
|
|
|
|
|
|
42 |
= -0,5 1,0 |
|
|
|
|
|
|
= 0 1,0 |
|
=0 1,2 |
=0 1,2 |
=0 1,3 |
|
1 |
|
|
|
|
|
|
2 |
|
2 |
2 |
2 |
|
X |
|
|
|
|
|
|
X |
|
X |
X |
X |
|
|
|
|
|
|
|
|
|
|
|
|
|

|
|
|
|
|
|
|
|
|
12 |
|
|
|
|
|
|
|
α = 28 |
0 ;h = 0,9;h |
= 0,9; ρ = 0,34754;C = C |
= 0,18438 |
|||||||||||
|
|
|
|
a |
|
f |
|
|
a |
|
a |
|
f |
|
|
Таблиця А. 4 -Значення коефіцієнтів зміщень X1, X2 |
|
|
|||||||||||||
|
Z1 |
Z2 |
|
20 |
25 |
|
31 |
34 |
42 |
50 |
65 |
|
100 |
150 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
20 |
-0,3 0 |
|
|
0,3 0,2 |
|
|
|
|
|
0,3 0,5 |
|
|
0,3 0,8 |
0,3 1,0 |
|
|
= |
|
|
- |
|
|
|
|
|
- |
|
|
- |
- |
|
|
1 |
|
|
= |
|
|
|
|
|
= |
|
|
= |
= |
|
|
X |
|
|
2 |
|
|
|
|
|
2 |
|
|
2 |
2 |
|
|
|
|
X |
|
|
|
|
|
X |
|
|
X |
X |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
25 |
= -0,5 0 |
|
|
|
-0,2 0,2 |
|
|
|
|
-0,2 0,5 |
|
|
-0,2 1,0 |
-0,2 1,2 |
|
|
1 |
|
|
|
= |
|
|
|
|
= |
|
|
= |
= |
|
|
X |
|
|
|
2 |
|
|
|
|
2 |
|
|
2 |
2 |
|
|
|
|
|
X |
|
|
|
|
X |
|
|
X |
X |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
31 |
0,5 0,2 |
|
|
|
|
|
0,2 0,3 |
|
|
0,2 0,5 |
|
|
0,2 1,2 |
0,2 1,3 |
|
|
= - |
|
|
|
|
|
= - |
|
|
= - |
|
|
= - |
= - |
|
|
1 |
|
|
|
|
|
2 |
|
|
2 |
|
|
2 |
2 |
|
|
X |
|
|
|
|
|
X |
|
|
X |
|
|
X |
X |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
34 |
= -0,5 0,3 |
|
|
|
|
|
|
-0,2 0,3 |
|
-0,2 0,6 |
|
|
-0,2 0,7 |
-0,2 1,5 |
|
|
1 |
|
|
|
|
|
|
= |
|
= |
|
|
= |
= |
|
|
X |
|
|
|
|
|
|
2 |
|
2 |
|
|
2 |
2 |
|
|
|
|
|
|
|
|
|
X |
|
X |
|
|
X |
X |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
42 |
= -0,5 0,5 |
|
|
|
|
|
|
|
-0,2 0,3 |
-0,2 0,5 |
|
|
-0,3 0 |
-0,2 1,2 |
|
|
1 |
|
|
|
|
|
|
|
= |
= |
|
|
= |
= |
|
|
X |
|
|
|
|
|
|
|
2 |
2 |
|
|
2 |
2 |
|
|
|
|
|
|
|
|
|
X |
X |
|
|
X |
X |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|

13
А.3.2 Внутрішнє зачеплення
α = 250 ;h = 1,0;h = 1,0; ρ = 0,35208;C = C |
= 0,20328 |
|||||||||
|
|
a |
f |
|
a |
|
a |
f |
|
|
Таблиця А.5 – Значення коефіцієнтів зміщення X2, X3 |
||||||||||
|
Z2 |
Z3 |
40 |
80 |
90 |
100 |
125 |
|
150 |
|
|
|
|
|
|
|
|
|
|
|
|
|
16 |
-0,4 0,5 |
|
|
|
|
0,8 2,0 |
|
0,8 1,0 |
|
|
|
= |
|
|
|
|
= |
|
= |
|
|
|
2 |
|
|
|
|
3 |
|
3 |
|
|
|
X |
|
|
|
|
X |
|
X |
|
|
|
|
|
|
|
|
|
|
|
|
|
20 |
-0,3 0,5 |
0,8 1,3 |
|
0,8 2,0 |
0,8 2,0 |
|
|
|
|
|
|
= |
= |
|
= |
= |
|
|
|
|
|
|
2 |
3 |
|
3 |
3 |
|
|
|
|
|
|
X |
X |
|
X |
X |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
32 |
-0,5 0,3 |
0,3 0,8 |
0,3 2,0 |
0,5 2,0 |
0,5 2,0 |
0,5 2,0 |
|
0,8 2,0 |
|
|
|
= |
= |
= |
= |
= |
= |
|
= |
|
|
|
2 |
3 |
3 |
3 |
3 |
3 |
|
3 |
|
|
|
X |
X |
X |
X |
X |
X |
|
X |
|
|
|
|
|
|
|
|
|
|
|
|
α = 280 ;ha = 0,9;hf = 0,9; ρa = 0,34754;Ca = C f
= 0,18438
Таблиця А.6 – Значення коефіцієнтів зміщення X2, X3
Z3 |
40, |
80 |
90, |
100, |
125, |
150 |
Z2 |
||||||
|
|
|
|
|
|
|
20 |
|
|
|
|
|
|
X2 = -1,0 0,5 |
X3 = 0,8 1,5 |
|
X3 = 0,8 2,0 |
|
||
|
|
|
|
|
|
|
32 |
|
|
|
|
|
|
X2 = -0,7 0,2 |
|
X3 = 0,6 2,0 |
|
|
||
|
|
|
|
|
|
|

14
Додаток Б
Визначення передаточного відношення та частот обертання зубчастих коліс редуктора
Б.1 Визначення передаточних відношень головного редуктора методом Віліса.
Розглядаємо тип редуктора 1А, варіант 1 (рис.Б.1). Визначення загального передаточного відношення редуктора здійснюється з використанням метода зворотного руху для диференціальної частини (колеса z1 z4)
U13(Н) = |
|
ω1 |
= |
ω1 −ωН = |
U1Н −1 |
|
|
|
|
|
|
U3Н −1 |
|
||||
|
ω3 |
|
ω3 −ωН |
(1) |
||||
та передаточного відношення для рядової частини (колеса Z4 Z6)
U |
46 |
= |
ω4 |
|
|
|
ω6 |
(2) |
|
|
|
|
3 |
6 |
z2 |
|
h |
z5 |
|
|
|
|
|
|
ϖ1 z1 z ϖh
Рисунок Б.1 - Головний редуктор 1А (АИ-20)
З урахуванням умови ω3=ω4 ,ωh=ω6 і рівнянь (1), (2) маємо
U1Н =1+U13( Н) (U 46 |
−1) =1− |
z3 |
|
(− |
z6 |
−1) = |
|||
z1 |
z4 |
||||||||
|
|
|
|
|
|
|
|||
=1− |
z1 + 2z2 |
(− |
z4 + 2z5 |
|
−1) = |
|
|||
z1 |
z4 |
|
|
||||||
|
|
|
|
|
|
||||
15
|
|
|
|
|
=1− |
20 + 2 25 |
|
(− |
20 + 2 25 |
−1) =16.75. |
||||||||||||||||||
|
|
|
|
|
|
|
20 |
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
20 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
Для варіантів 4, 5, 6 при визначенні передаточного відношення |
||||||||||||||||||||||||||
використовується |
|
умова |
|
|
|
|
ω3 = −ωh . |
В |
цьому випадку |
|||||||||||||||||||
U |
3H |
= |
ω3 |
|
= −1 і передаточне відношення редуктора матиме вигляд |
|||||||||||||||||||||||
ω |
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
H |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
20 + 2 25 |
|
|
|
||
U1Н =1+U13( Н) (U3H −1) =1+ 2 |
z3 |
=1+ 2 |
= 8. |
|
||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z1 |
20 |
|
|
|
|
||||||
|
|
Б.2 Визначення передаточного відношення головного редуктора |
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
енергетичним методом |
|
|
|
|
||||||||||||||||
|
|
U1Н |
=U16(Н) |
+U1(6)Н = |
z3 |
|
z6 |
|
|
+1+ |
z3 |
= =1+ |
z3 |
(1+ |
z6 |
) = |
||||||||||||
|
|
z1 |
z4 |
|
|
|
|
z1 |
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z1 |
|
|
|
z4 |
|||||||||
|
|
|
|
|
=1+ |
20 + 2 25 |
(1+ |
20 + 2 25 |
) =16.75 |
(3) |
||||||||||||||||||
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
20 |
|
|
|
|
|
|
20 |
|
|
|
|
|
|
|
|
|
|
||||
Б.3 Визначення частот обертання зубчастих коліс головного редуктора.
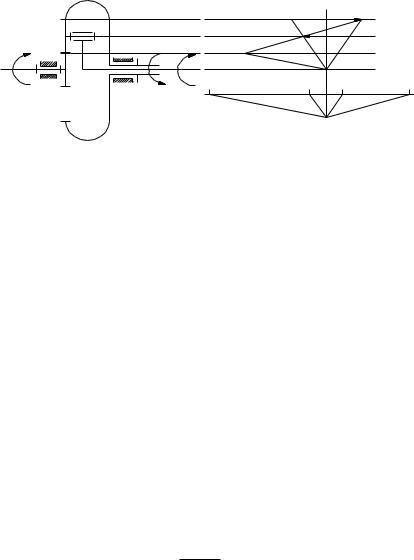
Визначення частот обертання коліс здійснюється з використанням картин швидкостей (рис.Б.2).
Будуємо кінематичну схему редуктора у масштабі µl (а), картину швидкостей у масштабі µv (б) та діаграму частот обертання
(в).
Далі, маємо
U1H = |
(0 −1) |
U12 = |
(0 −1) |
U13 = |
(0 −1) |
U15 = |
(0 −1) |
||||
|
; |
|
; |
|
; |
|
; |
||||
(0 − H ) |
(0 − 2) |
(0 −3) |
(0 −5) |
||||||||

16
Z 3 |
Z 6 |
|
|
|
|
|
|
|
|
h |
5 |
|
|
Z 2 |
Z 5 |
w h |
2 |
|
3,4 |
|
w 1 |
|
1 |
|
|
||
h |
|
|
|
|
||
Z1 |
Z 4 |
|
|
б |
|
|
1 |
5 |
h 0 3,4 |
2 |
|||
|
|
|||||
а |
|
|
|
в |
|
Рисунок Б.2 - Схема головного редуктора та картина швидкостей двигуна
Із рисунка Б2 маємо
U1H |
= |
587.43 |
|
= 16.319 ; |
|
U12 |
= |
|
587.43 |
|
= −1.161; |
||||||||||||||||||||||||||||
|
|
|
|
|
|
−505.98 |
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
36 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
U |
13 |
= |
|
587.43 |
|
|
= −4.08; |
|
U |
15 |
= |
|
587.43 |
|
= 5.015. |
||||||||||||||||||||||||
|
−145.12 |
|
117.14 |
|
|||||||||||||||||||||||||||||||||||
Далі |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
ω1 |
|
|
|
|
|
|
n1 |
|
|
|
|
|
ω1 |
|
|
|
|
|
|
|
n1 |
|
|
|
|
||||||||
U |
1H |
= |
= ± |
|
;U |
12 |
= |
|
= ± |
; |
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
ωH |
|
|
|
|
nH |
|
|
|
ω2 |
|
|
|
|
|
|
n2 |
|
(4) |
||||||||||||||||
|
U |
|
= |
|
ω1 |
= ± |
n1 |
;U |
|
|
= |
ω1 |
= ± |
n1 |
. |
|
|||||||||||||||||||||||
|
13 |
|
15 |
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
ω3 |
|
|
|
|
n3 |
|
ω5 |
|
|
|
|
|
n5 |
|
|
|||||||||||||||||
Використовуючи залежність ωi = |
π ni |
також відношення (4) |
|||||||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
30 |
|
|
|
|
|
|
|||
і ω =1200c−1 |
маємо: n |
|
|
=11459хв−1 ;n |
2 |
|
= 9871хв−1; |
||||||||||||||||||||||||||||||||
1 |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
п3 |
|
= 2809хв−1 ; п5 |
|
= 2285хв−1 ; пН = 702хв−1. |
|||||||||||||||||||||||||||||||||
17
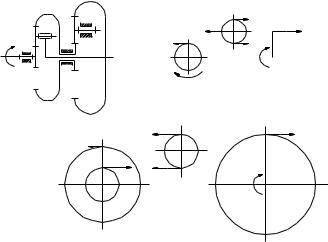
Для варіанта 4 картина швидкостей матиме такий вигляд
z 3
z 2 |
h |
|
|
ϖ1 z 1 |
|
|
|
ϖ3 ϖh 1 |
H 0 3 |
2 |
Рисунок Б.3 - Схема головного редуктора та картина швидкостей двигуна Д-27
Додаток В
Оптимізація параметрів редуктора
Оптимальні параметри редуктора (схема 1А, варіант 1) визначаються (в межах задач ТММ) із насупних умов:
1. На гвинті повинна бути забезпечена дозвукова швидкість, При прийнятих діаметра гвинта dГВ=4.5 м. число обертів гвинта і кутова
швидкість не повинні перевищувати nГВ <1051хв-1, ωГВ <110 c-1.
Тоді модуль передаточного відношення не повинен бути менше заданої величини
|
U ред |
|
= |
ωT |
= |
1200 |
= 10.91, |
||
|
|
||||||||
|
|
||||||||
|
|
|
|
ωгв |
|
110 |
|
||
де ωТ - кутова швидкість турбіни вибирається в залежності від від
варіанта завдання.
2. В редукторі не повинно бути циркулюючої потужності При виконанні цієї умови знаки крутних моментів на виходах основного і замикаючого контурів повинні бути одинакові
k = МОСН > 0 .
МЗАМ
18
3. В редукторі повинен виконуватись заданий розподіл потужності по контурам. При виконанні цієї умови, модуль відно-шення крутних моментів на виходах основного і замикаючого контурів повинен дорівнювати заданній величині
k = |
M осн |
|
|
= kзад |
|
|
|
|
|
|
M зам |
|
|
|
|
|
|||||
|
|
|
. |
|
|
|
|
|
||
|
|
|
|
|
|
|
||||
Вибір числа зубців коліс редуктора виконується на основі |
||||||||||
енергетичного методу розрахунку |
|
|
|
|
|
|
|
|
|
|
U ред = U1(h6) + U16(h) ; |
|
|
|
M |
h |
= |
U (6) |
|
||
|
|
|
|
|
1h |
, |
||||
|
|
|
M 6 |
U16(h) |
||||||
|
|
|
|
|
|
|
||||
де U1(h6) - передаточне відношення основного контура при
нерухомому замикаючому контурі (ω6 = 0 ); U16h - передаточне
відношення замикаючого контура при нерухомому основному контурі
(ωh = 0 ).
Для редукора (схема 1А, варіант 1) маємо
|
|
|
|
|
|
|
|
U1(6)H |
|
1 |
+ |
z3 |
|
|
|
|
U РЕД |
= 1 |
+ |
z3 |
(1 |
+ |
z6 |
); |
= |
z1 |
. |
||||||
|
|
|||||||||||||||
z1 |
z4 |
U16H |
|
|
|
|||||||||||
|
|
|
|
|
|
|
z3 z1 |
|
||||||||
z6 z4
Виконання умови (2) забезпечується зміною числа зовнішніх зачеплень у замикаючому контурі. Для даноі схеми ця умова виконується.
Виконання умов (1) і (3) забезпечується підбором числа зубців коліс. Однозначність рішення визначається найменшими розмірами редуктора. При цьому допускається коректування заданого значення
k.Для даної схеми, при ωT = 1200c−1 ,U РЕД = 10.91, kЗАД = 0.5
маємо систему рівнянь, з якої визначаються числа зубців коліс |
. |
||||||||||||
|
|
|
|
|
|
U1(6)H |
|
1+ |
z3 |
|
|
|
|
U РЕД |
= 1+ |
z3 |
(1+ |
z6 |
) = 10.91; |
= |
z1 |
|
= 0.5. |
|
|||
|
|
|
|
||||||||||
z1 |
z4 |
U16H |
|
z3 z1 |
|
|
|||||||
z6 z4
19
При одинакових мінімальних значеннях чисел зубців коліс z3 і z6 , що забезпечує мінімальні габарити редуктора, рішення рівнянь дає значення зубців коліс z1=z4=20; z2=z5=17; (z3=z6=54).
Додаток Г
Силовий розрахунок редуктора
Розглядаємо тип редуктора 1А, варіант 1 (рис.Г.1). Силовий
аналіз механізма розглядається |
при сталому режимі |
роботи |
||||
(ω = const ). У |
початкових |
даних |
використовуються: |
момент |
на |
|
входному валі |
редуктора – |
М1, |
радіуси ділильних |
кіл |
коліс |
- |
ri = 0.5 m zi . Приймаємо, що модулі усіх зубчастих коліс одинакові.
Числа зубців коліс пов’язані співвідношенням z3 = z1 +2z2 , z6 = z4 + 2z5. При розрахунках сили тертя в зубчатому зачепленні та підшипниках не враховуються. Розглядаються тільки тангенційні сили, що забезпечують передачу крутного моменту. Сили, що діють на колеса, визначаються із умови рівноваги ланок (рис.Г.1).
|
|
z3 |
z6 |
Fh2 2 |
F32 |
|
|
|
|
F2h |
|
|
z2 |
|
z5 |
F21 |
F |
|
h |
h |
|||
|
|
|
1 |
F12 |
|
|
|
|
|
||
M1 |
z1 |
|
z 4 |
M1 |
Mh |
|
|
|
|
|
F65 |
5 |
F56 |
|
F23 |
6 |
||
|
|||
F54 |
|
|
|
F45 |
|
|
|
3 |
|
M6 |
|
4 |
|
|
Рисунок Г.1 - Схема силового розрахунку редуктора

20
Із умови рівноваги сил, що діють на колесо 1, визначаємо
F = |
M1 |
. |
Із |
умови рівноваги |
сил, |
що |
діють |
на |
сателіт |
2, маємо |
||||||||||
12 |
r1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
F32 = F12 ; F23 |
= F21; Fh2 = −2 F12 ; F2h |
= 2 F12 . |
Із |
умови |
рівноваги |
|||||||||||||||
блока коліс 3,4 визначаємо |
F |
|
= −F |
|
r1 + 2 r2 |
; F |
= −F . Тоді, |
|||||||||||||
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
54 |
|
|
23 |
r4 |
|
|
45 |
54 |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
момент сил на водилі M h |
дорівнює |
|
M h = F2h (r1 + r2 ) , |
а сила на |
||||||||||||||||
колесі 4 |
F |
|
= − |
M1 (r1 + 2 r2 ) |
|
. Далі, |
і умови рівноваги колеса 5 |
|||||||||||||
|
|
|||||||||||||||||||
|
|
|
45 |
|
|
r1 r4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
визначаємо F65 = F45 ; F56 = −F65 . Тоді, |
момент сил на колесі 6 |
|||||||||||||||||||
дорівнює M |
6 |
= F |
(r + 2 r ) = |
M1 |
|
(r1 + 2 r2 ) (r4 |
+ 2 r5 ) |
. |
||||||||||||
|
|
|
||||||||||||||||||
|
|
|
|
56 |
4 |
5 |
|
|
r1 |
|
|
|
r4 |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
У цьому випадку моменти сил на водилі h і колесі 6 мають одинакові напрямки і співпадають з напрямком моменту M1 . Сумарний момент на вихідному валі редуктора дорівнює
M h6 |
= M h + M 6 |
= M1 |
( |
2 (r1 + r2 ) |
+ |
(r1 + 2 r2 ) (r4 + 2 r5 ) |
) = |
|
|
||||||
|
|
|
|
r1 |
r1 r4 |
||
= M1 (1−U13h (1−U 46 )) .
Знайдена величина сумарного моменту сил на вихідному валі редуктора дорівнює моменту сил на вхідному валі помноженому на передаточне відношення редуктора (додаток Б), що говорить про відсутність циркулюючих потужностей в редукторі.
Якщо підставити числові значення характеристик редуктора 1А, варіант 1, то отримаємо
F12 = 0.05M1 ; F2h = 20.05M1 ; M h = 20.05M1 (0.05 + 0.0625) = 4.5 M1;
