Nauchnaya_rabota_(1)

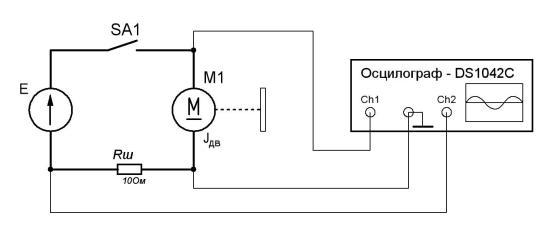
21

Формула для определения момента инерции двигателя с диском на ва-

лу имеет вид:

С целью определения коэффициента вязкого трения - Te и механическую по-

стоянную двигателя - C M для системы уравнений (4.10) был проведен эксперимент, схема которого изображена на рис. 4.7.

Рисунок 4.7 – Схема эксперимента для определения параметров двигателя

В ходе эксперимента на 9-й секунде ключ SA1 замыкался, на 21-й – размыкался. Графики напряжения двигателя Uдв и напряжения шунта Uш,

соответствуещие процессам разгона и выбега приведены на рис. 4.8.

22

Рисунок 4.8 – Графики напряжений двигателя и шунта

При Lя=0 схема замещения имеет вид, приведенный на рис. 4.9

Рисунок 4.9 – Схема замещения

Схема замещения показаная на рис. 4.9 описывается системой уравнений (4.10)

23

где I - ток в цепи якоря;

E- ЭДС источника питания;

- ЭДС двигателя;

RШ , RЯ , RSA1 - сопротивления шунта, якорной цепи и выключателя;

M ДВ , M С - момент двигателя и момент сопротивления;

- угловая скорость вращения двигателя; J дв - момент инерции двигателя с диском.

Данная система уравнений (4.10) внесена в среду Microsoft Excel, неиз-

вестные параметры системы уравнений Te , C M определены путем подбора

значений с помощью внешнего периферийного пульта, до визуального сход-

где mд – масса дебаланса, кг;

J дв - момент инерции двигателя, кг.м2;

l – расстояние от центра до дебаланса.

25

5 ИМИТАЦИОННАЯ МОДЕЛЬ ДВУХ ДЕБАЛАНСНЫХ ВИБРОПРИ-

ВОДОВ, РАСПОЛОЖЕННЫХ НА ОДНОЙ ПОДВИЖНОЙ ПЛАТ-

ФОРМЕ С УЧЕТОМ МОМЕНТА, ОБУСЛОВЛЕННОГО ДВИЖЕНИЕМ ОСИ ВРАЩЕНИЯ НЕУРАВНОВЕШЕННОГО ТЕЛА

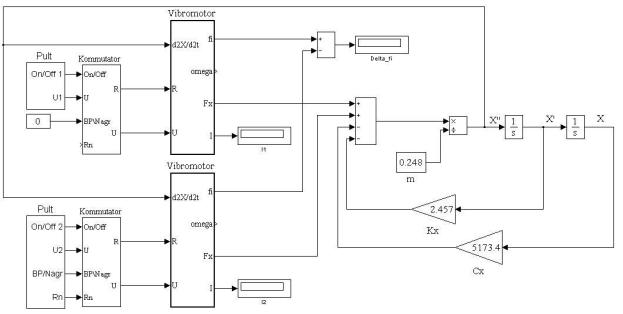
Имитационная модель, основанная на математическом описании (3.3) и

экспериментально определенных параметрах (таблица 4.3) приведена на рис 5.1.

Рисунок 5.1 – Имитационная модель совместной работы двух дебалансных виброприводов

Основными функциональными частями являются: механическая часть,

виброприводы (Vibromotor) и устройство управления (Pult, Kommutator). Мо-

дель дебалансного вибропривода, основанного на (3.1) приведена на рис 5.2.

26

Рисунок 5.2 – Имитационная модель дебалансного вибродвигателя

Модель функционального блока Kommutator, преобразующего управ-

ляющие воздействия оператора в изменение параметров и координат элек-

трической части вибродвигателя приведена на рис 5.3.

Рисунок 5.3 – Модель задатчика входных параметров

Управляющие воздействия оператора вводятся в модель с помощью внешнего периферийного устройства, подключенного к USB-порту (функ-

циональный блок Pult, рис. 5.1). Следует отметить, что предложенная имита-

ционная модель полностью адаптирована для подключения к ней системы управления (имеется в виду вход U функционального блока Vibromotor,

рис 5.1).

27

6 РЕЗУЛЬТАТЫ ФИЗИЧЕСКОГО ЭКСПЕРИМЕНТА И МАТЕМАТИ-

ЧЕСКОГО МОДЕЛИРОВАНИЯ

С целью подтверждения адекватности имитационной модели проведе-

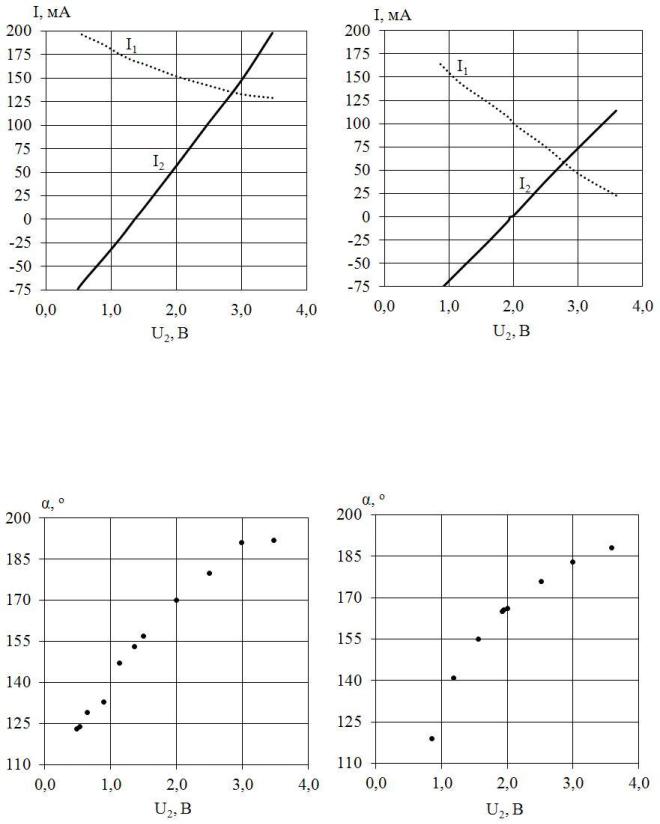
ны идентичные по сути математический и физический эксперименты. Для находящихся в режиме синхронизма двух дебалансных виброприводов при варьировании напряжения питания U2 фиксировались токи I1, I2 и разность углов поворота дебалансов α. Результаты экспериментов приведены в таблице 6.1 и на графиках (рис 6.1, рис 6.2).

Таблица 6.1 – Результаты экспериментов

Срыв синхронизации

Анализ зависимостей токов от напряжения U2 показал, что математиче-

ская модель отражает качественную картину взаимосвязей, обусловленных процессами передачи энергии между дебалансными вибродвигателями и платформой. Количественное несовпадение указанных зависимостей наибо-

лее вероятно связанно с допущениями о постоянстве коэффициента упруго-

сти и прямолинейном движении платформы вдоль одной оси, а также неуч-

тенными электрическими и механическими потерями.

28

а) б)

Рисунок 6.2 – Зависимость разности углов поворота от напряжения:

а) физический эксперимент; б) математический эксперимент.

29

ВЫВОДЫ

Предложенные для четырехдвигательного дебалансного вибропривода законы изменения углов поворота дебалансов обеспечивают регулирование как амплитуды так и направления возмущающей силы.

Разработанный лабораторный стенд позволяет наблюдать основные осо-

бенности работы дебалансных вибровозбудителей, а именно - синхро-

низацию дебалансов, вибрационное поддержание вращения и эффект Зом-

мерфельда, и может быть использован для первоначальной проверки алго-

ритмов управления.

Адекватное отражение имитационной моделью качественных зависимо-

стей основных электрических и механических координат исследуемой сис-

темы дает основания для использования полученной модели при разработке системы управления многодвигательным дебалансным виброприводом,

обеспечивающей независимое регулирование частоты, направления и ампли-

туды вибрации.

Полученный изменением напряжения питания второго двигателя диапа-

зон регулирования разности поворотов дебалансов (от 180° до 120°) состав-

ляет только треть от желаемого, следовательно, необходимы дальнейшие ис-

следования в направлении установления условий синхронного вращения де-

балансов за пределами указанного диапазона.

30

ПЕРЕЧЕНЬ ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ

1.Вибрации в технике: Справочник: В 6 т. – Москва: Машиностроение, 1970.

2.Вибрационные машины в строительстве и производстве строительных материалов: Справочник / Под ред. В.А. Баумана, И.И. Быховского и Б.Г. Гольдштейна. – Москва: Машиностроение, 1970.

3.Видинеев Ю.Д. Автоматическое непрерывное дозирование сыпучих материалов / Ю.Д. Видинеев. – Москва: 1974. – 120 с.

4.Карпин Е.Б. Средства автоматизации для измерения и дозирования массы / Е.Б. Карпин – М.: Машиностроение, 1971. – 469 с.

5.Спиваковский А.О. Вибрационные конвейеры, питатели и вспомогательные устройства / А.О. Спиваковский, И.Ф. Гончаревич. – М.: Машиностроение, 1972. – 328 с.

6. Потураев В.Н. Вибрационные транспортирующие машины /

В.Н. Потураев, В.П. Франчук, А.Г. Червоненко. – М.: Машиностроение, 1964.

–272 с.

7.Блехман И.И. Синхронизация в природе и технике.– Москва: Наука,

1981. – С. 49-50, 54-56.

8.Ярошевич М.П., Тимощук В.М., Силивонюк А.В. Самосинхронізація дебалансних збудників з кратними частотами обертання у вібраційних машинах з плоским рухом робочого органа // Автоматизація виробничих процесів у машинобудувані та приладобудуванні. – 2011. – № 45. – С.256262.

9.Блехман И.И. Что может вибрация?: О «вибрационной механике» и вибрационной технике.– Москва: Наука, 1988. – С. 163-171.

10.Мышкис А.Д. Лекции по высшей математике / А.Д. Мышкис – Москва: Наука, 1967. – 640 с.