
sm_rgr_2d
.pdf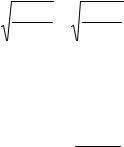
41
7.2.1.3Обираємо коефіцієнт зменшення допустимого напруження з
таблиць залежності ϕ=f(λ): ϕ1′ = 0.19 .
7.2.1.4Виконуємо перевірку на стійкість
σ = |
P |
|
= |
200 103 |
= 421 МПа > 160 МПа. |
|
ϕ1′ |
F |
0.19 2.5 10−3 |
||||
|
|
|
Оскільки напруження значно перевищує допустиме, то необхідно зробити ще одне наближення.
7.2.2Друге наближення
7.2.2.1 Розрахуємо коефіцієнт зменшення напруження
як середньо арифметичне
ϕ2 |
= |
ϕ1 +ϕ1′ |
= |
0.5 +0.19 |
= 0.345 . |
|
|
2 |
|
2 |
|
7.2.2.2 Визначення розмірів поперечного перерізу
Відповідно перерахуємо площу, діаметр труби, мінімальний радіус інерції
F = |
P |
200 103 |
|
= 3.62 10−3 м2=36.2 см2; |
|||
|
= |
|
|||||
ϕ2 [σ] |
0.345 160 106 |
||||||
|
d = |
F |
= |
36.2 |
= 8.49 см; |
||
|
|
|
0.16π |
|
0.16π |
|
|
imin=0.292d=2.48 см.
7.2.2.3Визначаємо гнучкість стержня
λ= μ l = 2 210 170 .
imin 2.48
42
7.2.2.4Обираємо новий коефіцієнт зменшення допустимого напруження
зтаблиць залежності ϕ=f(λ): ϕ2′ = 0.26 .
7.2.2.5Виконуємо наступну перевірку на стійкість
|
P |
|
200 103 |
|
σc = |
|
= |
|
= 212 МПа > 160 МПа. |
ϕ2′ F |
0.26 3.62 10−3 |
|||
Напруження перевищує допустиме на 32.5%, тому знову переходимо до наступного наближення.
7.2.3Наступне наближення
7.2.3.1 Розрахуємо коефіцієнт зменшення напруження, розмір поперечного перерізу та гнучкість стержня
|
|
|
|
|
ϕ3 = |
|
ϕ2 +ϕ2′ = |
0.345 +0.26 = 0.303 ; |
|
|
|||||||
|
|
|
|
|
|
|
|
2 |
|
|
2 |
|
|
||||
|
|
|
|
P |
|
|
|
|
200 103 |
|
|
||||||
F = |
|
|
|
= |
|
|
|
= 4.13 10−3 м2=4.13 см2; |
|
||||||||
ϕ3 [ω] |
0.303 160 106 |
|
|||||||||||||||
d = |
|
|
F |
|
= |
|
|
41.3 |
|
= 9.06 см. imin=0.292·9.06=2.64 см. |
|||||||
|
160π |
|
|
|
0.16π |
|
|
|
|
|
|
||||||
|
|
|
|
λ = |
μ l = |
2 210 |
159 . |
|
|
||||||||
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
i |
|
|
|
2.64 |
|
|
|
|
|
|
|
|
|
|
|
|
|
min |
|
|
|
|
|
|
|
|||
7.2.3.2 |
|
Обираємо |
|
коефіцієнт |
зменшення допустимого |
λ |
ϕ |
||||||||||
|
|
150 |
0.32 |
||||||||||||||
напруження з таблиць залежності ϕ=f(λ) |
|
|
|||||||||||||||
160 |
0.29 |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Більш точно табличний коефіцієнт ϕ визначаємо за допомогою ін-
терполяції |
|
|
|
ϕ3 |
= 0.32 − |
0.32 −0.29 |
9 = 0.293 . |
|
|
10 |
|

43
7.2.3.3 Виконуємо наступну перевірку на стійкість
σ = |
P |
|
= |
200 103 |
=165 МПа. |
|
ϕ3′ |
F |
0.293 4.13 10−3 |
||||
|
|
|
7.2.3.4Підраховуємо відносну похибку
δ= 160 −165 100% = 3% . 160
Похибка розрахунків задовільна і не перевищує ± 5%.
7.2.4 Розрахунок критичної сили та коефіцієнта запасу стійкості
Оскільки λ>λгр=100, то критичну силу розраховуємо за формулою Ейлера
|
π2 E I |
min |
|
π2 E F i2 |
π2E |
|
|
P = |
|
= |
min |
= |
λ2 |
F , |
|
|
|
|
|||||
кр |
(μ l)2 |
(μl)2 |
|
||||
де Imin =imin2 F ;
λ= μ l .
imin
Тоді |
P = |
3.142 2 108 |
4.13 10−3 = 322.14 . |
|
|||
|
кр |
1592 |
|
|
|
|
|
Коефіцієнт запасу стійкості |
|
||
nст = PPкр = 322200.14 =1.61 .
[1, С. 502−5064; 2, С. 46−471; 3, С. 492−496].
44
Типові задачі до розрахунково-графічної роботи №4
8 РОЗРАХУНКИ НА МІЦНІСТЬ З УРАХУВАННЯМ СИЛ ІНЕРЦІЇ
8.1Умова задачі
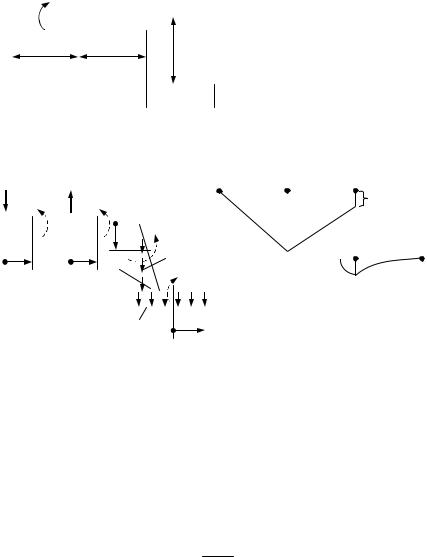
Валик і жорстко з’єднаний з ним ломаний стержень, такого ж поперечного перерізу, обертається з постійною швидкістю навколо осі АВ.
Необхідно:
а) побудувати епюру Mx від дії сил інерції, що виникають на вертикальній (СD) і горизонтальній (DЕ) ділянках ломаного стержня;
б) знайти допустиме число обертів валика (АВ) за хвилину, при допустимому навантаженні [σ]=100 МПа і γ=78 кН/м3.
|
Розрахункові |
схеми і вихідні |
дані |
наведені |
на рисунку 8.1 і |
|||
в таблиці 8.1. |
|
|
|
|
|
|
||
|
Таблиця 8.1 − Вихідні дані |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
№ |
l, см |
|
Діаметр валика |
№ |
l, см |
|
Діаметр валика |
|
рядка |
|
d, мм |
рядка |
|
d, мм |
|||
|
|
|
|
|||||
1 |
|
15 |
|
21 |
6 |
40 |
|
16 |
|
|
|
|
|
|
|
|
|
2 |
|
20 |
|
22 |
7 |
45 |
|
17 |
|
|
|
|
|
|
|
|
|
3 |
|
25 |
|
23 |
8 |
50 |
|
18 |
|
|
|
|
|
|
|
|
|
4 |
|
30 |
|
24 |
9 |
55 |
|
19 |
|
|
|
|
|
|
|
|
|
5 |
|
35 |
|
25 |
0 |
60 |
|
20 |
|
|
|
|
|
|
|
|
|
Примітки. 1. Для спрощення обчислень рекомендується виконувати їх спочатку у загальному вигляді, позначаючи інтенсивність сил інерції через q.
2. Рівнодійні сил інерції на горизонтальних і вертикальних ділянках, опорні реакції, ординати епюри Mх потрібно виразити через ql і ql2.

|
|
|
|
|
|
45 |
|
|
|
|
|
|
|
А |
|
C |
|
B |
|
А |
|
|
C |
|
B |
|
|
|
|
|
|
|
|
|
|
|
||
I |
|
l |
D |
|
|
VI |
|
|
l |
D |
|
|
|
|
|
|
|
|
E |
|
|
|
E |
||
|
|
l |
|
l |
E |
|
|
l |
|
l |
||
|
|
|
|
|
|
|
|
|||||
|
А |
|
B |
C |
|
А |
|
B |
|
C |
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
l |
|
||
II |
|
|
l |
|
|
VII |
|
|
E |
D |
E |
|
|
|
|
D |
|
|
|
||||||
|
|
|
E |
|
|
|
|
|
|
|||
|
|
2l |
l |
|
|
l |
|
l |
l |
|
||
|
|
|
|
|
|
|
||||||
|
|
l |
|
l |
|
|
|
|
l |
|
l |
|
|
А |
|
C |
|
B |
|
А |
|
|
C |
|
B |
III |
l |
|
|
VIII |
|
|
|
|||||
|
D |
|
|
|
|
|
l |
|
|
|||
|
|
E l/2 l/2 |
E |
|
|
|
|
E l/2 D |
|
|||
|
l |
|
2l |
|
l |
|
|
|
l |
|
l |
|
|
C |
|
|
|
C |
|
А |
|
|
|
|
C |
IV |
А |
l |
B |
IX |
|
|
B |
|
l |
|||
|
|
|
|
|||||||||
|
D |
D |
|
|
|
|
|
|||||
|
l/2 |
E |
|
E |
l/2 |
|
|
|
|
E l/2 D |
||
|
|
2l |
|
l |
C |
|
|
|
l |
|
l |
|
|
|
|
|
|
|
А |
|
|
C |
|
B |
|
V |
|
|
|
|
|
X |
|
|
|
|||
А |
|
B |
l |
|
|
l |
|
|
||||
|
E |
|
|
D |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
E l/2 |
|
E |
||
|
|
|
|
D l/2 |
|
|
|
|
||||
Рисунок 8.1 −Розрахункові схеми
46
8.2Приклад розрахунку
А |
|
|
ω |
B |
C |
|
|
Вихідні дані: |
|||
|
|
|
|
|
|
|
|
|
|
[σ]=100 МПа; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
l |
|
|
l |
|
l |
|
|
γ=78 кН/м3; |
|
|
|
|
|
|
|
|
|
|
|
l=40 см; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
D |
|
|
E |
d=20·мм. |
|
|
|
|
|
|
|
|
l |
|||
|
|
|
|
|
|
|
|
|
|
|
|
 A
A
8.2.1 |
Встановлюємо |
закон зміни інтенсивності сил інерції і |
||||||||||||||||||||
|
|
|
|
визначаємо реакції опор |
|
|
|
|
|
|
|
|||||||||||
|
|
RA |
|
|
|
|
RB Mx |
|
|
|
A |
|
B |
|
C |
|
|
|||||
A |
|
Mx |
|
C |
|
|
|
|
|
|
|
½ |
|
|
||||||||
|
|
Mx |
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
z |
|
|
|
|
|
|
|
|
|||||
|
|
|
B |
|
|
|
|
|
|
|
|
|
D |
E |
||||||||
|
|
z |
|
z |
|
q(z) |
|
2 |
½ |
|
||||||||||||
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
q |
|
|
Mx |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
½ |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
D |
|
|
E |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
q |
z |
Епюра Mx, (ql2) |
|
|
|||||||
Ділянка CD: |
|
|
|
0≤z≤l. |
|
|
|
|
|
|
|
|||||||||||
|
|
q(z)= |
γ F |
ω2 z |
|
|
лінійний закон. |
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
g |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
При z=0; |
|
|
q(0)=0; |
z=l; |
q(l)= |
γ F |
ω2 l . |
|
|
|||||||||||
|
|
g |
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ділянки DЕ: Всі точки стержня знаходяться на однаковій відстані l від осі обертання, тому
qDE = q = γ gF ω2 l .
47
|
|
|
∑M A = 0; RB l − |
1 ql 2l − ql |
5 l = 0; RB= 7 ql; |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
2 |
|
|
2 |
|
|
|
|
|
∑M B |
= 0; R A l − |
1 ql l − ql |
3 l =0; RA = 2ql. |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
2 |
|
|
|
|
Перевірка: ∑Pвер = 0; |
|
RB−RA − ql |
− |
1 ql = 0; |
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
7 ql −2ql − |
3 ql = 0. |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
2 |
|
|
|
|
8.2.2 Визначаємо згинальні моменти на кожній ділянці |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
Ділянка ЕD: |
|
0≤z≤l. |
|
|
|
|||||||
M x |
+ qz |
z |
; |
|
M x |
= − |
qz |
2 |
|
квадратична парабола. |
|
||||||||||||
2 |
|
|
2 |
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
При z=0 |
|
Mx=0; |
при z=l |
|
|
M x = − |
ql2 |
епюру будуємо на |
|||||||||||||||
|
|
|
2 |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
стиснутих волокнах. |
|||
|
|
|
|
|
|
|
|
|
|
|
Ділянка CD: |
|
0≤z≤l. |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
M |
x |
− R l |
+ R |
A |
2l = 0; |
|
M |
x |
= 7 ql2 |
−4ql2 = −1 ql2 |
const. |
||||||||||||
|
|
B |
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
2 |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
Ділянка AВ: |
|
0≤z≤l. |
|
|
|
|||||||
M x = −RA z . |
|
|
При z=0 |
|
Mx=0; |
при z=l |
M x = −2ql2 . |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
Ділянка BC: |
|
0≤z≤l. |
|
|
|
|||||||
M |
x |
= R z − R |
A |
(l + z). |
При z=0 |
M |
x |
= −2ql2 ; |
при z=l |
||||||||||||||
|
|
B |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
M x = − |
1 ql2 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|

48
За одержаними даними будуємо епюру Mx, звідки знаходимо максимальний момент
|
|
M xmax |
= |
|
2ql2 |
. |
|
|
|
|
|
|
|
|
||||||
8.2.3 Із умови міцності визначаємо допустиме число обертів валика |
||||||||||||||||||||
|
|
σmax = |
M xmax |
|
≤ [σ]. |
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
Wx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Враховуючи, що |
|
q = |
γF |
ω |
2 |
l |
3 |
Wx = |
πd 3 |
; |
F = |
πd |
2 |
|||||||
|
g |
|
|
|
|
32 |
4 |
, |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
запишемо |
|
|
M x |
|
|
= |
|
2γπd 2 |
|
ω2l3 . |
|
|
|
|
||||||
|
|
max |
|
|
|
4g |
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Тоді отримуємо |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
σmax = 2γ |
πd 2 |
ω2l |
3 |
|
32 |
|
|
= 16γω2l3 |
≤[σ], |
|
|
|
||||||||
4 |
πd 3 |
|
|
|
|
|||||||||||||||
|
g |
|
|
|
|
|
|
|
gd |
|
|
|
|
|
||||||
звідки [ω]= |
g d [σ] |
= |
9.81 0.02 100 |
|
|
=15.67 с-1. |
|
|
|
|||||||||||
|
16 γ l3 |
16 78 10−3 0.43 |
|
|
|
|
|
|
|
|
||||||||||
Допустиме число обертів валика |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
[n]= [ω] 30 = |
15.67 30 |
|
=149.67 об./хв. |
|
|
|
|
||||||||||||
|
π |
|
|
π |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
[1, С. 605−610; 2, С. 52−53; 3, С. 534−537].

49
9 ВИЗНАЧЕННЯ НАПРУЖЕНЬ В ДВОТАВРОВИХ БАЛКАХ ПРИ УДАРНОМУ НАВАНТАЖЕННІ
9.1 Умова задачі
На двотаврову балку, яка закріплена на двох жорстких опорах, з висоти h падає вантаж Р.
Необхідно:
а) визначити найбільше напруження в небезпечному перерізі балки;
б) розв’язати аналогічну задачу за умови, що праву опору замінюємо пружиною, піддатливість якої дорівнює α;
в) порівняти отримані результати.
Розрахункові схеми |
і вихідні |
дані |
наведені |
на рисунку 9.1 і |
||||||||
в таблиці 9.1. |
|
|
|
|
|
|
|
|
|
|
||
Таблиця 9.1 − Вихідні дані |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
№ |
№ |
|
l, |
|
Р, |
|
h, |
|
α·103, |
||
|
рядка |
двотавра |
|
м |
|
Н |
|
см |
|
м/кН |
|
|
|
1 |
|
20 |
|
2.1 |
|
1100 |
|
11 |
|
21 |
|
|
2 |
|
20а |
|
2.2 |
|
1200 |
|
12 |
|
22 |
|
|
3 |
|
24 |
|
2.3 |
|
300 |
|
3 |
|
23 |
|
|
4 |
|
24а |
|
2.4 |
|
400 |
|
4 |
|
24 |
|
|
5 |
|
27 |
|
2.5 |
|
500 |
|
5 |
|
25 |
|
|
6 |
|
27а |
|
2.6 |
|
600 |
|
6 |
|
26 |
|
|
7 |
|
30 |
|
2.7 |
|
700 |
|
7 |
|
27 |
|
|
8 |
|
30а |
|
2.8 |
|
800 |
|
8 |
|
28 |
|
|
9 |
|
33 |
|
2.9 |
|
900 |
|
9 |
|
29 |
|
|
0 |
|
36 |
|
3.0 |
|
1000 |
|
10 |
|
30 |
|

|
|
|
50 |
|
h |
Р |
|
h |
Р |
I |
|
|
VI |
|
|
l/5 |
4l/5 |
3l/4 |
l/4 |
h |
Р |
|
h |
Р |
II |
|
|
VII |
|
|
l/4 |
3l/4 |
4l/5 |
l/5 |
h |
Р |
|
h |
Р |
III |
|
|
VIII |
|
|
|
|
|
|
|
l/3 |
2l/3 |
4l/5 |
l/5 |
|
h |
Р |
h |
Р |
IV |
|
|
IX |
|
|
l/2 |
l/2 |
3l/4 |
l/4 |
|
h |
Р |
h |
Р |
V |
|
|
X |
|
|
2l/3 |
l/3 |
2l/3 |
l/3 |
Рисунок 9.1 −Розрахункові схеми
