
sm_rgr_2d
.pdf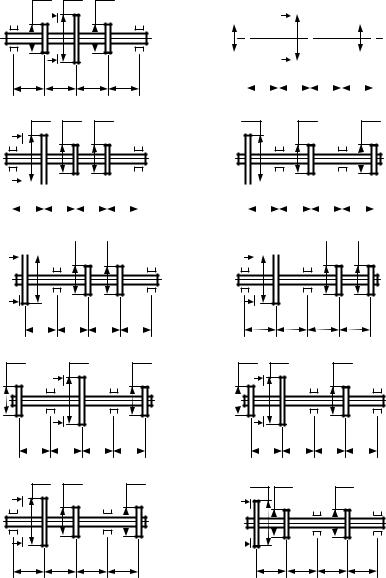
21
I |
D2 |
D1 |
D2 |
|
|
|
|
I |
|
|
|
|
a |
I b |
c |
a |
|
II |
D1 |
|
D2 |
D2 |
|
|
I |
|
|
|
|
VI D2 |
D1 |
|
|
|
|
D2 |
|||||||||||||
|
|
|
|
|
|
|
|
I |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
I |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
a |
b |
|
|
c |
|
|
a |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
VII D1 D2 D2
|
|
I |
|
|
|
|
|
|
|
b |
c |
b |
|
|
|
|
|
|
|
|
|
b |
|
|
|
|
|
|
|||||
|
|
a |
|
|
|
|
|
|
|
|
a |
c |
|
a |
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
III |
|
D1 |
|
|
|
|
D2 |
D2 |
VIII |
|
|
|
|
D1 |
|
D2 |
|
D2 |
|||||||||||||||
|
I |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
I |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
I |
a |
|
b |
c |
b |
|
I b |
c a/2 a/2 |
|||
IV |
D2 |
|
|
D1 |
|
D2 |
IX |
D2 D1 |
D2 |
|
||
|
|
|
I |
|
|
|
|
|
I |
|
|
|
|
|
a |
I |
b |
c |
b |
|
|
I |
a/2 |
b |
b |
|
|
|
|
|
a/2 |
|||||||
V |
I |
D1 |
|
D2 |
|
D2 |
X |
D1 D2 |
D2 |
|
||
|
|
|
|
|
|
|
I |
|
|
|
|
|
|
I a |
b |
c |
a |
|
I |
a |
b |
c |
a |
||
Рисунок 4.1 − Розрахункові схеми

|
|
|
|
|
|
22 |
|
|
|
|
|
|
4.2 |
Приклад розрахунку |
|
|
|
|
|
I − I |
|||||
Вихідні дані: N=100 кВт; |
n=1000 об/хв; |
|
|
|
|
|
||||||
|
а=b=1 м; |
D1=1 м; |
D2=0.5 м; |
T1=2t1 |
t2 |
T2=2t2 |
||||||
|
α |
=60°; α =30°. |
|
|
|
|
α2 |
|||||
|
1 |
|
|
2 |
|
|
|
|
|
α1 |
t1 |
|
|
I |
|
|
|
|
|
|
|
|
|
||
|
|
D1 |
|
D2 |
|
|
D2 |
|
|
|
||
|
|
|
|
|
|
|
|
|
||||
а) |
|
|
|
|
|
|
A |
|
|
B |
|
|
|
I |
|
|
|
|
|
|
|
|
|
||
|
|
a/2 |
a/2 |
|
b |
|
b |
|
|
|
||
|
Mкр1 |
|
Р1гор |
Mкр2 |
RA |
HA |
|
B |
HB |
y |
||
б) |
|
|
|
|
|
Mкр |
2 |
|
|
z |
||
Р1вер |
Р2гор Р2вер |
|
|
A Р2гор |
|
RB |
|
|
||||
|
|
|
Р2вер |
|
х |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0.955 |
|
0.955 |
|
|
0.4775 |
|
|
|
|||
|
|
|
|
|
|
|
|
|
еп. Мкр, кН·м |
|||
в) |
|
|
|
|
|
|
|
|
|
|||
Площина YZ |
Р1вер |
Р2вер |
|
RА |
|
Р2вер |
RВ |
|
||||
|
|
|
|
|
|
|
|
|
|
еп. Мх, кН·м |
||
г) |
|
|
2.481 |
|
|
|
|
1.765 |
|
|
|
|
|
|
|
|
|
|
6.394 |
|
|
|
|
||
|
|
|
Р1гор |
Р2гор |
|
Р2гор |
|
|
|
|||
Площина ХZ |
|
НА |
|
НВ |
|
|||||||
д) |
|
|
|
|
|
|
|
|
|
еп. Мy, кН·м |
||
|
|
1.432 |
0.384 |
|
2.673 |
|
|
|
||||
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
6.405 |
3.203 |
|
|
|
|
е) |
|
|
2.865 |
|
|
|
|
еп. Мзг, кН·м |
||||
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|||
|
|
0 |
|
1 |
|
2 |
|
3 |
4 |
|
|
|
|
Рисунок 4.2− Розрахункова схема, епюри Мх, Мy, Мкр, Мзг |
|
|
|||||||||

23
4.2.1 Визначити Мкр на шківах D1 і D2
Мкр1=9.55N/n=0.955 кНм;
Мкр2=0.5Мкр1=0.4775 кНм.
4.2.2 Визначити колові зусилля t1, t2 і радіальний тиск на вал P1 та P2
|
|
|
2Mкр |
|
2 0.955 |
|
||
t |
= |
1 |
|
= |
|
|
=1.91 кН; |
|
|
|
|
|
|||||
1 |
|
|
D1 |
|
|
1 |
|
|
|
|
|
|
|
|
|||
t |
= |
2Mкр2 |
|
= 2 0.4775 =1.91 кН; |
||||
|
||||||||
2 |
|
|
D2 |
|
|
0.5 |
|
|
|
|
|
|
|
|
|||
P1=3t1=3·1.91=5.73 кН; |
P2=3t2=3·1.91=5.73 кН. |
|||||||
4.2.2.1 Визначити зусилля, які діють в горизонтальній і вертикальній площинах
P1гор=P1·cos α1=5.73·cos 60°=2.865 кН; Р1гор |
|
|
Р2гор |
|
P2гор=P2·cos α2=5.73·cos 30°=4.962 кН; |
|
α1 |
α2 |
|
P1вер=P1·sin α1=5.73·sin 60°=4.962 кН; |
Р1 |
|
Р2вер |
Р2 |
|
|
Р1вер |
|
|
P2вер=P2·sin α2=5.73·sin 30°=2.865 кН.
4.2.3Показати на розрахунковій схемі усі зусилля, які діють на вал, і визначити опорні реакції (рис. 4.2, б)
4.2.3.1 Вертикальна площина
|
|
|
(2b + a)+ P |
|
|
a |
|
|
|
P |
3b + |
|
|
||||
|
2 |
|||||||
∑M B = 0; RA = |
1вер |
2вер |
|
|
|
= |
||
|
|
2b |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
= |
4.962 3 +2.865 3.5 |
=12.457 кН; |
||||||
|
||||||||
|
|
|
2 |
|
|
|
|
|

24
∑PY = 0; |
RB = P1вер +2P2вер − RA = 4.962 +2 2.865 −12.457 = |
|||||||||
|
= −1.765 |
кН |
− |
направлена |
|
вниз, напрям змінюємо |
||||
|
|
|
|
на протилежний. |
|
|
|
|||
4.2.3.2 |
Горизонтальна |
площина, |
яку |
для |
зручності суміщаємо |
|||||
з вертикальною площиною |
|
|
|
|
|
|
|
|
|
|
|
|
P |
(2b |
+ a)− P |
|
3b + |
a |
|
||
|
|
|
|
|
||||||
|
|
2 |
||||||||
∑M B = 0; H A = |
1гор |
|
|
2гор |
|
|
|
= |
||
|
|
2b |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
||
|
= 2.865 3 −4.962 3.5 |
= |
|
|
|
|||||
|
|
|
|
2 |
|
|
|
|
|
|
|
= −4.386 |
кН − |
направлена |
ліворуч; |
||||||
∑PX = 0; |
НB = H A + P1гор −2P2гор = 4.386 +2.865 −2 4.962 = |
|||||||||
|
= −2.673 |
кН |
− |
направлена |
ліворуч,тобто не |
|||||
|
|
|
|
співпадає |
з |
попереднім напрямом. |
||||
4.2.4Побудувати епюру Мкр (рис. 4.2, в)
4.2.5Визначити згинальні моменти в вертикальній і горизонтальній площинах для характерних перерізів і побудувати епюри Мх і Мy (рис. 4.2, д; 4.2, г)
4.2.6Побудувати сумарну епюру згинальних моментів, попередньо визначивши їх величину в характерних точках 1, 2, 3 (рис. 4.2, е)
M зг(1) = M X2 |
+ MY2 = 2.4812 +1.4322 = 2.865 кН·м; |
M зг(2) |
= 6.3942 +0.3842 = 6.405 кН·м; |

25
M зг(3) =  1.7652 +2.6732 = 3.203 кН·м.
1.7652 +2.6732 = 3.203 кН·м.
Примітка. Необхідно пам’ятати, що вектор моменту Мзг в різних перерізах може мати різні напрями, внаслідок чого епюра Мзг може бути криволінійною (рис. 4.2, е; ділянки 1−2, 2−3).
4.2.7 Визначити небезпечний переріз і величину M pIII у цьому перерізі
Для нашого прикладу це переріз в т. 2 (опора А), де
Мкр=0.4775 кН·м; Мзг=6.405 кН·м.
Тому
MpIII =  M зг2 + Mкр2 =
M зг2 + Mкр2 =  6.4072 +0.47752 = 6.423 кН·м.
6.4072 +0.47752 = 6.423 кН·м.
4.2.8Визначити діаметр вала
d = 3 |
32M pIII |
= 3 |
32 6.423 10−3 |
= 9.78 10−2 |
м. |
|
π[σ] |
3.14 70 |
|||||
|
|
|
|
Округлюючи розрахунковий діаметр до стандартних величин, передбачених ГОСТ 6636-69, одержимо − d=100 мм.
[1, С. 338−342; 2, С. 42−45; 3, С. 377−384].
26
5 ПОБУДОВА ЕПЮР Qy, Mx І ЛІНІЇ ПРОГИНІВ W(Z) ДЛЯ СТАТИЧНО НЕВИЗНАЧУВАНИХ НЕРОЗРІЗНИХ БАЛОК
5.1 Умова задачі
Статично невизначувана балка навантажена розподіленим та зосередженим зусиллям.
Необхідно:
а) розкрити статичну невизначуванність балки і визначити реактивні зусилля (в долях ql);
б) побудувати епюри перерізуючих сил Qy та згинаючих моментів Мх;
в) побудувати епюри прогинів W та обчислити три координати у прольоті і дві − на консолі.
Розрахункові |
схеми |
та вихідні дані |
наведені |
на рисунку 5.1 |
||||
і в таблиці 5.1. |
|
|
|
|
|
|
||
Таблиця 5.1 − Вихідні дані |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
№ |
|
Коефіцієнти |
№ |
Коефіцієнти |
|
||
|
|
|
|
|
|
|
||
|
рядка |
|
α |
β |
рядка |
α |
β |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
1 |
|
0.1 |
1.0 |
6 |
0.6 |
1.5 |
|
|
|
|
|
|
|
|
|
|
|
2 |
|
0.2 |
0.9 |
7 |
0.7 |
0.4 |
|
|
|
|
|
|
|
|
|
|
|
3 |
|
0.3 |
0.8 |
8 |
0.8 |
0.3 |
|
|
|
|
|
|
|
|
|
|
|
4 |
|
0.4 |
0.7 |
9 |
0.9 |
0.2 |
|
|
|
|
|
|
|
|
|
|
|
5 |
|
0.5 |
0.6 |
0 |
1.0 |
0.1 |
|
|
|
|
|
|
|
|
|
|

I
II
III
IV
V
27
q P=αql
A
 VI l βl
VI l βl
|
P=αql |
q |
|||||
|
|
|
A |
|
|
VII |
|
|
|
|
|
|
|||
|
l/2 |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
l/2 |
|
βl |
|
||
|
|
|
|
||||
|
|
|
|
|
|
|
|
q P=αql |
|
P=αql |
|||||
|
|
|
|
|
A |
||
|
|
|
|
|
|||
|
l/2 |
|
|
|
|
|
VIII |
|
|
|
|
|
|
||
|
|
l/2 |
|
βl |
|
||
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
q |
|
P=αql |
||
|
|
|
|
|
A |
||
|
|
|
|
|
|||
P=αql |
|
|
|
|
|
IX |
|
|
|
|
|
|
|||
|
|
|
|
|
|
||
|
l/2 |
|
l/2 |
|
βl |
|
|
|
|
|
|
|
|
|
|
|
P=αql |
q |
|||||
|
|
|
|
|
|
|
X |
|
|
|
|
|
|
|
|
|
l/2 |
|
A |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|||
|
|
l/2 |
|
βl |
|||
|
q |
|
|
|
|
|
|
|
|
A |
|||
|
|
|
||||
l |
|
|
|
βl |
|
|
|
|
|
|
|
||
|
|
|
|
|
||
|
|
|
|
|
||
|
|
|
||||
|
|
|
|
P=α |
|
ql |
|
|
|
|
|||
|
|
|
q |
|||
|
A |
|
|
|
|
|
|
|
|
|
|
||
P=αql |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
l/2 |
l/2 |
|
βl |
|
|
|
|
|
|
|
|
|
|
q P=αql |
|
|
|
|
||
|
|
|
A |
|||
|
|
|
||||
l/2 |
|
|
|
P=αql |
|
|
|
|
|
||||
l/2 |
|
|||||
|
βl |
|
|
|||
|
|
|
|
|
|
|
q |
|
|
|
|
|
|
|
|
|
A |
|||
|
|
|
||||
P=αql |
|
|
|
P=αql |
|
|
|
|
|
|
|
||
|
|
|
||||
|
|
|
||||
l/2 |
l/2 |
|
βl |
|
|
|
|
|
|
|
|
|
|
|
|
|
q |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A |
|
|
|
|
|
P=αql |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
l/2 |
l/2 |
|
βl |
|||
Рисунок 5.1 − Розрахункові схеми

|
|
|
|
28 |
|
|
|
|
|
5.2 |
Приклад розрахунку |
|
|
|
|
|
|
||
Вихідні дані: α=1; |
β=1. |
|
|
|
|
|
|
||
|
y |
|
I |
q |
RA |
|
|
P=αql |
|
|
MO |
|
II |
|
|
||||
а) |
O |
z |
|
|
А |
|
z |
В |
z |
I |
|
|
|
||||||
|
RO |
|
|
II |
|
||||
|
|
|
|
|
|
|
|||
|
|
|
l |
|
|
βl |
|
|
|
|
|
|
|
1.0 |
|
|
|
1.0 |
|
|
|
|
|
|
|
|
|
епюра Qy, |
|
б) |
0.875 |
|
|
|
|
|
|
(ql) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1.875 |
|
|
|
|
|
0.375 |
|
|
|
|
|
|
епюра Mx, |
|
в) |
|
|
|
|
|
|
|
||
|
|
|
1.0 |
|
|
|
(ql2) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0.0151 |
0.032 |
|
|
|
епюра W, |
||
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
(ql4/ЕІ) |
|
г) |
|
|
|
|
0.067 |
|
|
|
|
|
|
l/3 l/3 l/3 |
l/2 |
|
|
0.55 |
|
||
|
Рисунок 5.2− Розрахункова схема, епюри Мх, Qy та W(г) |
|
|
||||||
29
Статичну невизначуванність розв’язуємо за допомогою рівнянь статики та метода початкових параметрів.
5.2.1Визначаємо момент та реакцію на лівій опорі МО і RО
Для цього складаємо два рівняння.
5.2.1.1 Рівняння статики у вигляді суми моментів всіх зовнішніх зусиль відносно правої опори А (рис. 5.2, а)
∑M A = 0; MO + RO l − ql2 |
+ ql2 = 0 , |
(5.1) |
2 |
|
|
де P·β·l=ql2.
5.2.1.2 Рівняння метода початкових параметрів для першої ділянки
(рис. 5.2, а)
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
M |
O |
z2 |
|
R z3 |
|
q z4 |
|
|
|
||||
EI W |
= EI W |
|
+ EI |
x |
ϕ |
O |
z + |
|
|
|
|
|
+ |
|
O |
− |
|
. |
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
x z |
|
x O |
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
6 |
|
24 |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
При z=0 |
W(O)=0; ϕО=0 (закріплення). |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
При z=l |
W(l)=0 (опора). Тоді |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
M |
|
l2 |
|
|
|
R |
|
l3 |
|
|
ql4 |
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
O |
|
|
|
|
+ |
|
|
O |
|
|
|
− |
24 |
= 0 . |
|
|
|
|
|
(5.2) |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Із рівняння 5.2 визначаємо |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
R |
|
|
|
= − |
3MO |
+ ql . |
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
O |
|
|
|
|
|
|
|
l |
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Із рівняння 5.1 визначаємо |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
ql |
− |
3MO |
|
|
− |
ql2 |
+ ql |
2 |
|
= 0 ; MO |
= |
3ql2 |
= 0.375ql |
2 |
. |
|||||||||||||||
MO + |
l |
l |
|
|
2 |
|
|
|
|
8 |
|
|||||||||||||||||||
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Тоді RO=−0.875·ql − напрям RО змінюємо на протилежний.
30
5.2.2 Визначаємо реакції RA
∑MO = 0; RA l − MO − ql2 |
−2ql2 = 0; |
RA = 2.875ql. |
|||||||
|
|
|
|
|
2 |
|
|
|
|
5.2.3 Визначаємо Qy і Мх |
|
|
|
|
|
||||
Ділянка ОА, переріз І–І: |
|
|
|
|
0≤z≤l. |
qz2 |
|
||
Qy=−RO−qz; Мx=MO−RO·z− |
; |
||||||||
2 |
|||||||||
|
|
|
|
|
|
|
|
||
z=0; |
Qy=−RO=0.875ql; Мx=MO=0.375ql2; |
||||||||
|
Q |
y |
= −0.875ql |
− ql = −1.875ql; |
|||||
z=l; |
|
|
|
|
|
|
|
||
|
|
|
2 |
|
|
|
|
||
|
|
|
|
. |
|
|
|
||
|
M x = −ql |
|
|
|
|
||||
Ділянка АВ, переріз ІІ–ІІ: |
|
|
|
0≤z≤l. |
|
|
|||
Qy=q·l; Мx=−q·l z;
z=0; Qy=q·l; Мx=0; z=l; Qy=q·l; Мx=−q·l2.
За відомими даними будуємо епюри Qy та Мx (рис. 5.2; б, в).
5.2.4Визначення прогинів балки
Початок координат системи yz вибираємо в закріпленні (точка О).
Тоді початкові параметри WO і ϕО дорівнюють нулю (WO=0; ϕО=0) і рівняння прогинів набирає вид
|
|
|
|
|
|
|
|
|
|
|
|
M |
O |
z2 |
|
R |
z3 |
|
q z4 |
|
|||||||
Ділянка ОА: |
0≤z≤l. |
EI W |
z |
= |
|
|
|
|
|
− |
O |
|
|
|
− |
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
x |
|
|
2 |
|
|
|
|
|
6 |
|
|
|
24 |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ql4 |
|
|||||
1. z=0; |
W(O)=0. |
|
|
|
|
3. |
z = |
|
2l |
; |
W |
2l |
= 0.032 |
. |
|||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
EIx |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
ql4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2. |
z = |
|
l; |
W |
|
= 0.0151 |
|
. |
|
4. |
z=l; |
|
W(l)=0. |
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
3 |
|
1 |
|
EIx |
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
l |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
