Як правило, визначається у відсотках
.
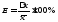(1.6)
Знайти істинне значення фізичної величини х неможливо. Можна тільки вказати на інтервал (хmin, хmax), в якому з ймовірністю знаходиться значення досліджуваної величини.
Приклад:
поглядом вимірюють зріст студента в
сантиметрах. Ми можемо припустити, що
зріст студента може бути визначений
між 1,5 м і 2,0 м з ймовірністю 0,9. Тоді ми
можемо стверджувати, що зріст студента
може бути визначений між 1,6 м і 1,8 м з
меншою ймовірністю 0,6 і так далі. Цей
інтервал називають довірчим
інтервалом.
На рис.1.1
зображено довірчий інтервал досліджуваної
величини x,
де
–
найбільш ймовірне значення виміряної
величини;Δх
– півширина довірчого інтервалу для
заданого .
Тому, істинне значення вимірюваної
величини може бути визначене як
,
(1.7)
з ймовірністю , або
.
(1.8)
Рисунок 1.1
Ймовірність
знаходження істинного значення
вимірюваної величини в інтервалі
x
залежить від кількості вимірювань n.
Якщо
,
то ймовірність наближається до 1. Якщо
жn
дорівнює
кільком одиницям, то ймовірність не
досягає й 0,6. Тому для малої кількості
вимірювань згаданий інтервал розширюють,
збільшуючи Δx.
Для цього знаходять середньоквадратичну
похибку середнього арифметичного
,
(1.9)
і збільшують її в t раз (t – так званий коефіцієнт Ст`юдента. Цей коефіцієнт було введено в 1908 році англійським математиком та хіміком В.С. Госсетом). Величину
,
(1.10)
називають випадковим відхиленням. Середнє квадратичне похибка результату серії вимірювань, викликана випадковими відхиленнями xi, визначається як
.
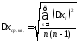(1.11)
Множимо знайдене значення коефіцієнта Стьюдента t (коефіцієнт Стьюдента, залежить від і кількості вимірів n) на середню квадратичну похибку середнього значення, знаходимо випадкову похибку Δхвип результатів прямих вимірювань
.
(1.12)
Таблиця 1.1
|
n\α |
0,4 |
0,5 |
0,6 |
0,7 |
0,8 |
0,9 |
|
2 |
0,73 |
1,00 |
1,38 |
2,0 |
3,1 |
6,3 |
|
3 |
0,62 |
0,82 |
1,06 |
1,4 |
1,9 |
2,9 |
|
4 |
0,58 |
0,77 |
0,98 |
1,3 |
1,6 |
2,4 |
|
5 |
0,57 |
0,74 |
0,99 |
1,2 |
1,5 |
2,1 |
|
6 |
0,56 |
0,73 |
0,92 |
1,2 |
1,5 |
2,0 |
|
7 |
0,55 |
0,72 |
0,91 |
1,1 |
1,4 |
1,9 |
|
8 |
0,55 |
0,71 |
0,90 |
1,1 |
1,4 |
1,9 |
|
9 |
0,54 |
0,71 |
0,89 |
1,1 |
1,4 |
1,9 |
|
10 |
0,54 |
0,70 |
0,88 |
1,1 |
1,4 |
1,8 |
|
20 |
0,58 |
0,69 |
0,86 |
1,1 |
1,3 |
1,7 |
|
∞ |
0,52 |
0,67 |
0,84 |
1,0 |
1,3 |
1,6 |