1.7.2. Робота випрямляча на активно-індуктивне навантаження з кінцевою індуктивністю

Режим: α=0, r0, L_a≠0, 0<L_d<∞

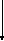
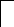
VS ≡ Ld Rd е2 i2=iV=id VT La ra ~ е2 VS R L U1

L_d вмикають в коло навантаження для сглажування струму.

Еквівалентний активний опір та індуктивність ланцюга

У відповідності з другим законом Кірхгоффа

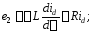
де

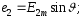
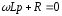- характеристичне рівняння.

Звідки

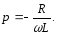
Рішення будемо шукати у вигляді

де i_cв – вільна складова,

i_np – вимушена складова.

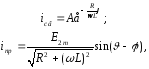
де

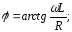
А знайдемо з початкових умов.

При

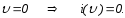
Тоді

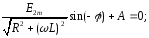
Звідки

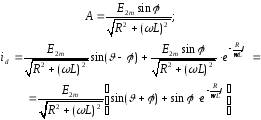
Позначимо

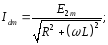
Тоді

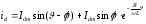
U, I

Знайдемо енергію, що запасена в індуктивності L за період

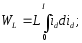
Енергія, яку накопичує індуктивність

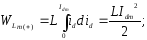
Енергія, яку віддає індуктивність

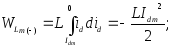
Таким чином, протягом періоду

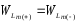
Постійна складова випрямленої напруги

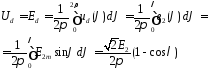
Постійна складова випрямленого струму

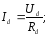
λ можна визначити з умови: при 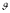=0;  i_d = 0

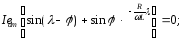
Якщо L_d збільшиться, λ також збільшиться, а I_dm зменшиться, отже, K_pl зменшиться. Таким чином, L_d можна використовувати як фільтр струму на стороні навантаження.

1.7.3 Робота випрямляча на активно-ємкісненавантаження

Режим: α=0, r_a=0, L_a=0, L_d=0, 0<С<∞.

i1 VT UV i2=iV UV Ud=Uc id Rd ≡ U1 U2 ~ iv e2 ic C ic C iR Rd

Рівняння, що описують електричні процеси в схемі:

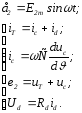
Позначимо:

λ – тривалість протікання струму.

φ – кут затримки включення вентиля відносно точки природного запалення.

На інтервалі:

1). 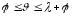- ключ замкнутий (вентиль відкритий).

U_T=0;

Знайдемо i_T.

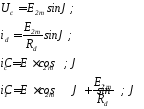
2) 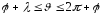-ключ розімкнений.

.

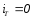По другому закону Кірхгоффа

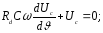
Характеристичне рівняння

.

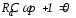Корінь рівняння

.

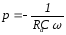Тоді напруга на конденсаторі

.

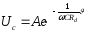Струм навантаження

.

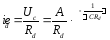Струм конденсатора

.

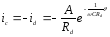Напруга на вентилі

.

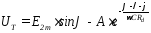Постійну А визначимо з умови

При

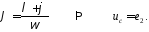
Тоді

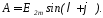
Визначимо λ+φ

при

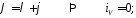
Відповідно до графіка зміни функції

.

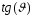
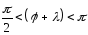При активному навантаженні: X_c → ∞, С → 0, (φ+λ) → π.

При ємнісному навантаженні: R_d → ∞, (φ+λ) → .

З умови сталого режиму, тобто періодичності електромагнітних процесів в схемі, знайдемо φ.

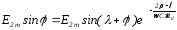
Дане трансцендентне рівняння можна вирішити чисельним методом або графічно.

e,u e,i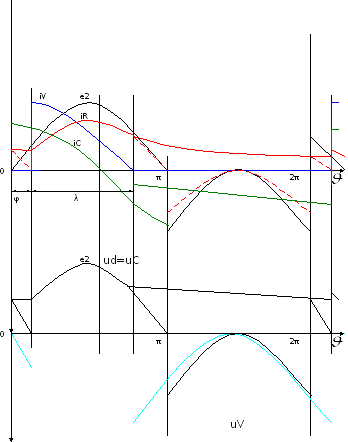

Рис. Діаграма електричних процесів в однофазній однонапівперіодній схемі випрямляча з активно-ємкісним навантаженням.

1.8. Однофазний двонапівперіодний випрямляч з нульовим виводом

Випрямляч з нульовим виводом по суті є двофазним, оскільки вторинна обмотка трансформатора з нульовою точкою створює дві ЕРС, рівні по величині, але протилежні по напряму.

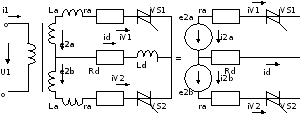
1.8.1. Робота однофазної нульової схеми на активне навантаження

Режим: L_a=0, L_d=0, r_a=0, 0<α<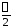

iV1 uV1 iV1, iV2 u, i

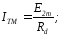
Середня випрямлена напруга

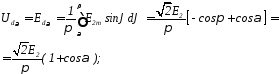
Це регулювальна характеристика

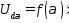
При α = 0

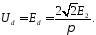
звідки

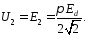
Максимальна зворотня напруга

U_RM = 2E_2m = πE_d0.

Середній випрямлений струм

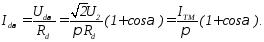
При α = 0

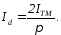
Звідки

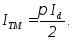
Очевидно, що завантаження тиристорів і трансформатора при активному навантаженні максимальне при α=0. Це видно з діаграм, тому вимоги до тиристорів і трансформатора визначимо за цієї умови.

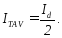
Струм вторинної обмотки трансформатора при α = 0

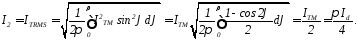
Визначимо струм первинної обмотки трансформатора

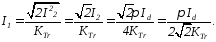
Визначимо S₁, S₂, S_T

;

.

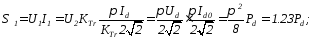
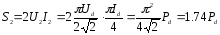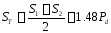K_pl – визначаємо самостійно.

Зовнішня характеристика U_d = f (I_d)

U_dα = E_dα – (r_a + r_T) I_d,

де r_T – динамічний опір вентиля в прямому напрямі (вважаємо за постійний)

E_dα– ЭРС холостого ходу,

При I_dα = 0  U_dα = E_dα .

Коефіцієнт використання трансформатора по потужності

,

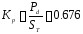що вище, ніж в однонапівперіодній схемі більш ніж в 2 рази, оскільки немає вимушеного намагнічення і К_Р→1 при α = 0 оскільки трансформатор не завантажений вищими гармоніками струму i₁.