Де γ – контур, що охоплює всі полюсы функціїX(z). Співвідношення(3.8) зворотне z- перетворення.

Приклад: Нехай задане Z- перетворення вхідного сигналу.

Потрібно знайти вихідний сигнал.

Функція x(z) (x(z)=(z+1)/z) аналитична на всій площині, за винятком т. z=0. Звертаючи до формули (3.8), знайдемо:

В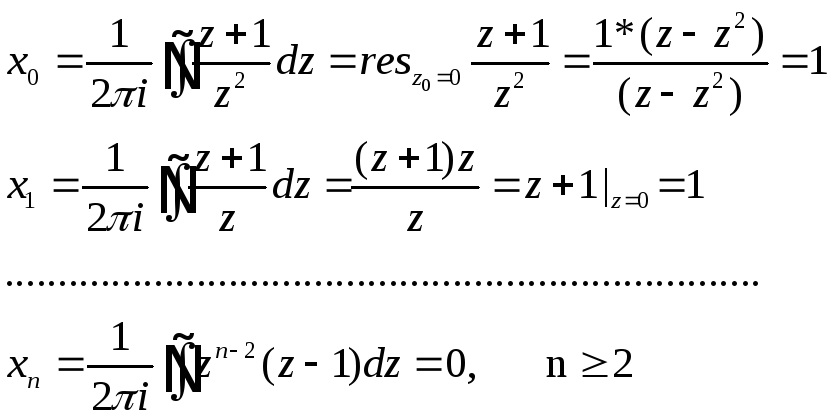ихідний сигнал має видx(n)=(1,1,0,0,0,…)...

Розглянемо найважливіші властивості Z-перетворення: вони аналогічні властивостям Лапласа:

1. Лінійність.

Якщо X₁(n) і X₂(n) – числові послідовності, що відображають дискретні сигнали Z-перетворення, що мають, _X1(z) і _X2(z), то лінійна комбінація сигналів

X₃(n)=a₁x₁(n)+a₂x₂(n) має Z-перетворення у виді лінійної комбінації їхніх Z-перетворень.

2. Теорема зсуву. (Z-перетворення зміщеного сигналу)

Нехай x₂(n) отриманий з x₁(n) зсувом останнього убік запізнювання на одну позицію: x₂(n)=x₁(n-1).

Безпосереднє обчислення Z-перетворення приводить до результату:

X₂(z)=x₁(z)z^-1, при запізнюванні на m позицій:

X₂(z)=x₁(z)z^-m, еквівалентно множенню перетворення на z^-m.

3. Теорема про згорток.

Z-перетворення дискретної згортки 2-х послідовностей дорівнює добутку Z-перетворень цих послідовностей:

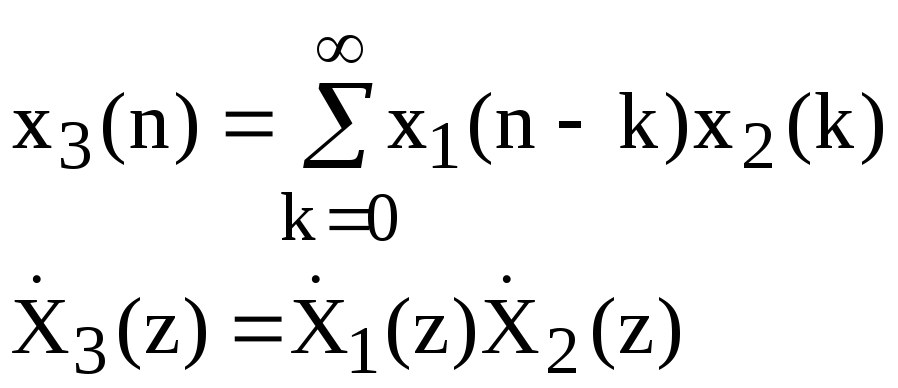На підставі викладених властивостей сформулюємо алгоритм аналізу ЛЦФ методом Z-перетворення.

Користаючись теоремою про згорток, можна записати Z-перетворення вихідного сигналу через добуток Z-перетворень вхідного сигналу й імпульсної характеристики ЛЦФ.

Визначення. Z-перетворення імпульсної характеристики називають передатною функцією ЛЦФ чи його системною функцією.

За аналогією з рівнянням згортки сигналів у часовій області

для перебування вихідної послідовності Y(z)=G(z)X(z) необхідно визначити:

1. Z-перетворення вхідної послідовності x(n)

2. Передатну функцію G(z) по відомій імпульсній характеристиці g(n)

3. Z-перетворення вихідної послідовності

4. Саму вихідну послідовність

за допомогою теореми про лишки.

Способи визначення передатної функції ЛЦФ.

1. Прямим Z-перетворенням імпульсної характеристики ЛЦФ:

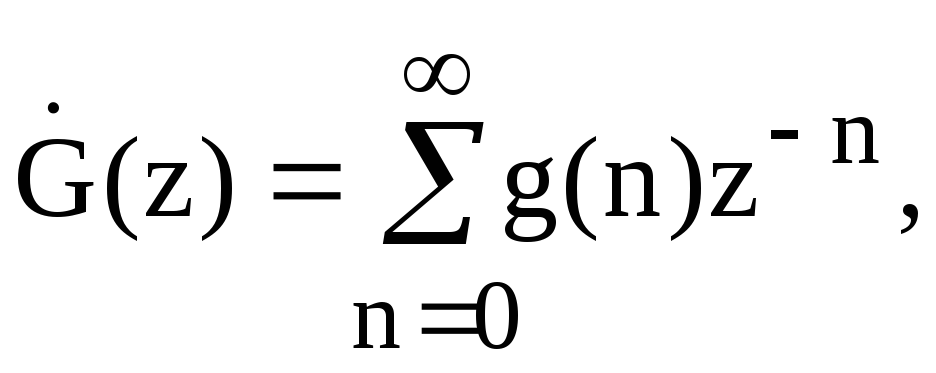2. По різницевому рівнянню.

Нехай рекурсивний ЛЦФ описується різницевим рівнянням виду:

Застосувавши до рівнянняZ-перетворення, одержимо.

Кожна з напівнескінченних сум дорівнює: (користаючись властивістю лінійності і теоремою зсуву)

д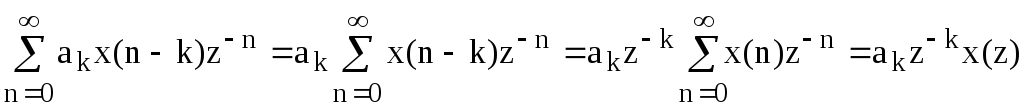ля трансверсальної частини суми.

для рекурсивної частини суми.

Таким чином, Z-перетворення різницевого рівняння:

Маємо передатну функцію ЛЦФ:

Вираження (3.10) має велике значення, тому що зв'язуючи передатну функцію і різницеве рівняння ЛЦФ, дозволяє вирішити також і зворотню задачу – по передатній функції ЛЦФ G(z) знайти його різницеве рівняння і по ньому побудувати структурну схему фільтра. Задачі подібного типу (установлення структури по характеристиках) звуться задач синтезу, чи в даному випадку задач реалiзацii ЛЦФ.

По вираженню типу (3.10) будується різницеве рівняння виду

Приклад: Реалізуємо фільтр із передатною функцією

G(z)=(2z^-1+1)/(4z^-2+4z^-1+2).

Розділивши вираження на коефіцієнт при z^-1 у чисельнику, маємо

Тобто M=1; a₀=0.5; a₁=1; N=2; b₁=-2; b₂=-2, і

Побудуємо по різницевому рівнянню структурну схему ЛЦФ.

Рис.3.1

Приклад. Знайдемо вихідний сигнал методом Z-перетворення побудованого ЛЦФ. Подамо на його вхід послідовність x(n)=(1/2)ⁿ і визначимо y(n).

1. Z-перетворення вхідної послідовності

2. Як пам'ятаємо, передатна функція

3. Z-перетворення вхідного сигналу:

4) Вихідна послідовність сигналу:

З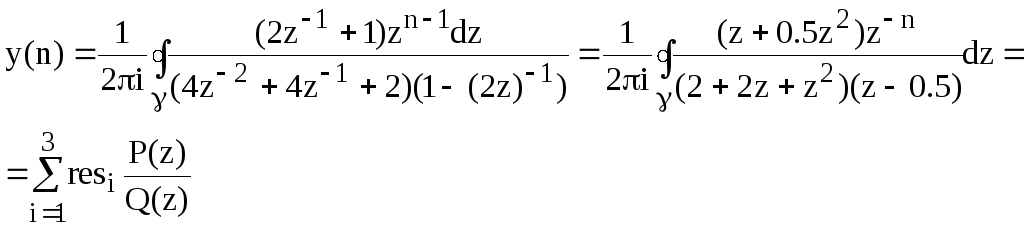найдемо полюси підінтегральної функції – корені знаменника: 2+2z+z²=0,

z-0.5=0, тоді z₃=0.5

Знайдемо лишки:

Представляючи комплексні числа в показовій формі *ρe^iφ знайдемо

В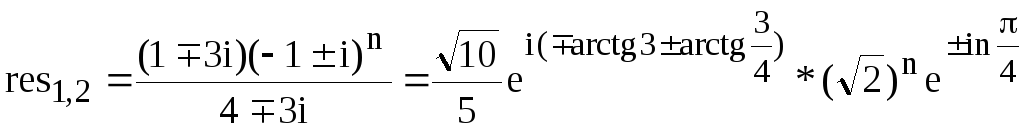ихідна послідовність як сума лишкiв res₁, res₂, res₃ дорівнює:

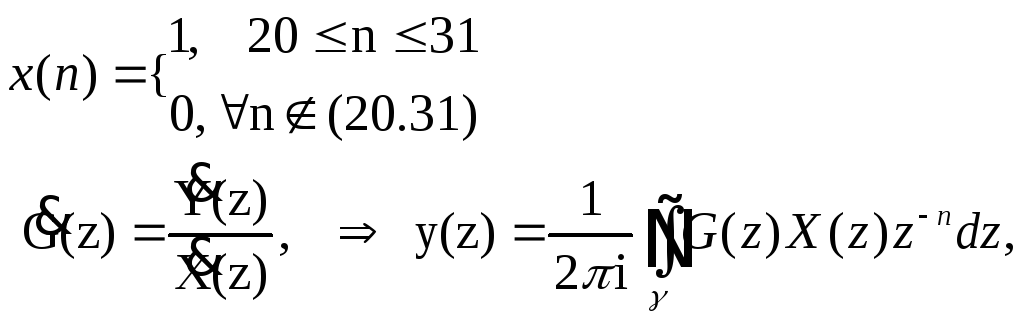
Знайти y(n), якщо

Приклад Нехай дана передатна функція ЛЦФ у виді

хоча легше в даному випадку побудувати y(n) по різницевому рівнянню, користаючись передатною функцією:

y(n)=x(n)+1*x(n-1)-0.5y(n-1)-0.421y(n-2)

Побудуємо структурну схему ЛЦФ по різницевому рівнянню.

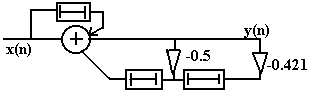Рис.3.2

Розрахунок ЛЦФ (перетворення y(n) по x(n)) можна реалізувати у виді програми розрахунку y(n) по різницевому рівнянню, задаючи у виді масиву x(n) – вхідну послідовність і знаходячи масив y(n) – вихідну послідовність.

Опис лабораторної установки

Лабораторна установка складається з комп’ютера і програмного забезпечення у вигляді двох середовищ аналізу і проектування –математичного процесора MathCad і програми моделювання електронних схем Electronis Work Bench.

Розрахункове завдання

1. Методом різницевих рівнянь, користуючись математичним процесором MathCad, розрахувати для схеми, що наведено на рис.3.1, сигнал з виходу ЛЦФ, якщо на вхід подається сигнал

2. ЛЦФ завданий своєю передавальною (системною) функцією G(z)=. Синтезувати електричну схему фільтра. Визначити його імпульсну характеристику g(n).визначаються номером залікової книжки:-останній,.-передостанній і т.д.

3. По схемі на рис.3.2 знайти імпульсну характеристику ЛЦФ і для вхідної дії у вигляді 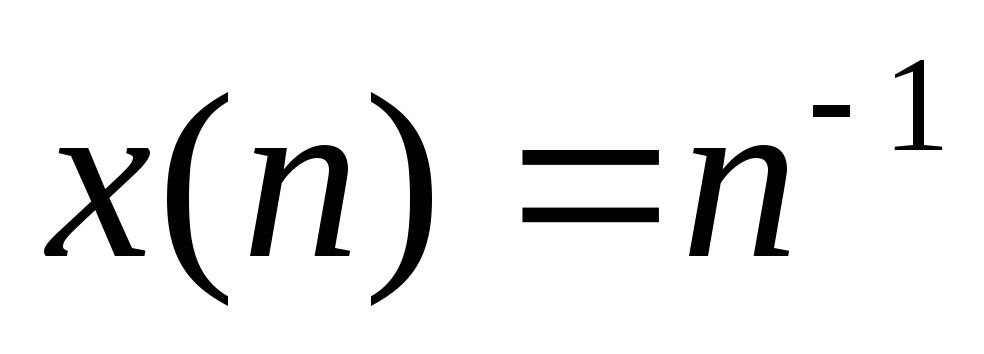методом дискретної згортки знайти відгукy(n).

4. Методом z-перетворень знайти відгук ЛЦФ, що завданий своєю імпульсною характеристикою . Синтезувати схему фільтра. Визначити передавальну функціюG(z).

5. Змоделювати ЛЦФ у програмному середовищі Electronics Work Bench.

Лабораторне завдання

Наступні завдання виконуються за допомогою математичного процесора MathCad. Всі графіки побудувати для перших тридцяти дискретних відліків часу n.

1. ЛЦФ задається своєю передавальною функцією 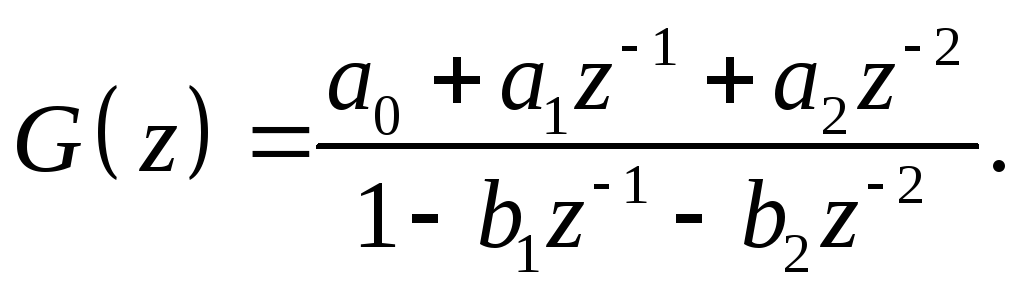Знайти різницеве рівнянняy(n), імпульсну характеристику g(n), синтезувати електричну схему. Побудувати графіки.

2. Імпульсна характеристика ЛЦФ має вигляд: . Побудувати електричну схему. Для зовнішньої дії типузнайти відгук фільтраy(n). Побудувати графіки.

3. Побудувати схеми рекурсивного та нерекурсивного ЛЦФ другого порядку. Знайти по них імпульсну та перехідну характеристики цих фільтрів.

4. Для схеми ЛЦФ, зображеної на рис.3.1, знайти амплітудно – частотну та фазо – частотну характеристики і побудувати їх.

5. Знайти умови, при виконанні яких ЛЦФ, що зображений на рис.3.2, стає цифровим резонатором.

6. Методом z – перетворень проаналізувати ЛЦФ, схема якого зображена на рис.3.2. На вході діє сигнал 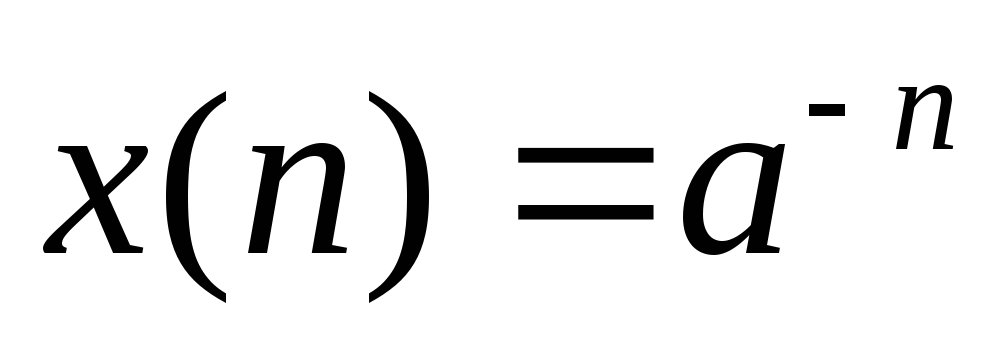. Знайти імпульсну, перехідну характеристики та передавальну функцію цього фільтра.

Вимоги до звіту

Звіт повинен вміщувати в собі:

1. Результати розрахунків та виконання лабораторного завдання.

2. Всі вхідні і вихідні послідовності повинні бути відображені графічно як дискретні функції часу.

3. Для кожного ЛЦФ потрібно навести електричну схему

Контрольні запитання

1. Що таке лінійний цифровий фільтр? Різновиди ЛЦФ.

2. Запишіть різницеве рівняння рекурсивного та нерекурсивного ЛЦФ.

3. Побудуйте канонічну схему ЛЦФ другого порядку. Поясніть принцип її формування , записавши різницеві рівняння та їх z- перетворення.

4. Запишіть системну функцію ЛЦФ. Як вона пов’язана із імпульсною характеристикою?

5. Зв’язок між комплексним коефіцієнтом передачі і системною функцією.

6. Запишіть зв’язок між імпульсною та перехідною характеристиками ЛЦФ.

7. Поясніть, чому амплітудно- та фазо-частотні характеристики ЛЦФ є періодичними функціями частоти.

8. Як отримати вихідний сигнал, маючи імпульсну характеристику і знаючи вхідну дію?

9. Умови фізичної реалізованості ЛЦФ.

10. Аналіз ЛЦФ методом z- перетворень.

11. Аналіз ЛЦФ методом аналітичного розв’язку різницевих рівнянь.