1.4 Класифікація середовищ

Властивості середовища характеризуються параметрами . Параметрносить назвупитомої провідності середовища . Розрізняють такі середовища:

– лінійні, в яких параметри не залежать від величини електричного і магнітного поля;

– нелінійні, в яких параметри або хоча б один із них, залежить від величини електричного і магнітного поля.

Всі реальні середовища нелінійні. В подальшому при слабких полях середовище, яке розглядається, буде вважатися лінійним.

Лінійні середовища поділяються на однорідні, неоднорідні, ізотропні, анізотропні:

однорідні – середовища у яких параметри середовища не залежать від координат;

неоднорідні– хоча б один параметр являється функцією координат;

ізотропні – якщо властивості середовища однакові у всіх напрямках. В цих середовищах вектори ,, а також,. Параметри– скалярні величини;

анізотропні – якщо властивості різні в різних напрямках. В таких середовищах перераховані вектори електромагнітного поля (ЕМП) можуть бути не паралельними, якщо , або хоча б один з них, являєтьсятензором.

“Тензор” походить від латинського “tensus” (напружений). Це математичний об’єкт, який узагальнює скалярні і векторні величини, матриці і т.д. В кожній системі координат тензор задається сукупністю чисел, взятих в певному порядку. В тривимірному просторі – це сукупність дев’яти величин.

В кристалічному діелектрику являється тензором. В загальному випадку він записується у вигляді матриці:

. (1.35)

При цьому форма рівнянь (1.16) залишається тією ж:

. (1.36)

В декартовій системі координат кожна проекція вектора запишеться у вигляді лінійної комбінації всіх трьох проекцій вектора:

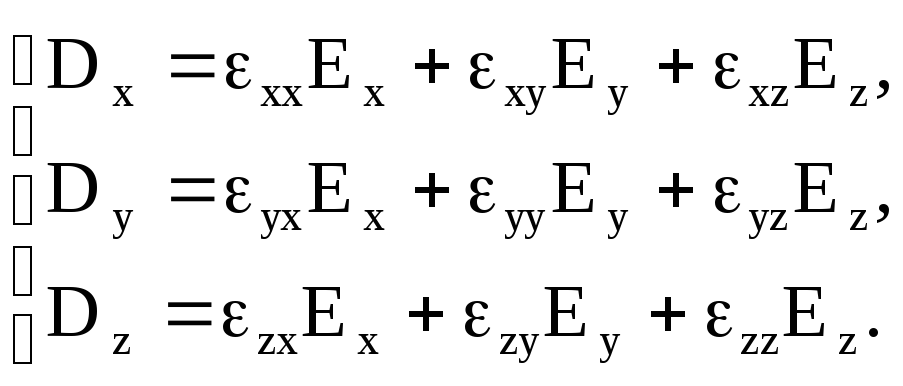(1.37)

Непаралельність векторів електричного поля і(а такожі) в анізотропному середовищі пояснюється наявністю кута (відмінним від 0 і) між вторинним полем в результаті поляризації і первинним електричним полем.

У феромагнітних середовищах тензором буде магнітна проникність . Запис дляаналогічний (1.35). При цьому форма рівняння (1.32) зберігається:

. (1.38)

Розписуючи (1.38) в проекціях на осі декартової системи координат , приходимо до формул, аналогічних (1.37).

В ряді випадків тензором може бути і питома провідність .

2 Основні рівняння електромагнетизму

В розділі 1 було з’ясовано, що шість векторів ,,,,,характеризують ЕМП. Всі електромагнітні процеси підлягають законам, які вперше сформулював у вигляді диференційних рівнянь Джордж Максвел в 1873 р. Ці рівняння були отримані в результаті узагальнення експериментальних даних і мають назву “Рівняння Максвела”. Незважаючи на те, що фізика за останні століття просунулась далеко вперед в розумінні природи електромагнетизму, рівняння Максвела все одно служать міцним фундаментом тих областей науки, які пов’язані з практичним використанням електромагнітних явищ.

2.1 Зведення рівнянь Максвела

Приведемо з довідковою метою систему рівнянь Максвела, кожне з яких будемо окремо розглядати в подальшому.

Таблиця 2.1

	Інтегральна форма		Диференційна форма
1
2
3
4
Матеріальні рівняння
5. 6.7. , ,
Наслідок рівнянь Максвела
Закон збереження заряду 8. або		Рівняння неперервності 9. або

В таблиці 2.1 приведені рівняння, які складають основу теорії електромагнетизму. Всі величини, які входять в ці рівняння, є функції координат і часу t. Частіше всього, при розв’язку задач електродинаміки, використовують рівняння Максвела в диференційній формі. Операції rot і div в них – це комбінації частинних похідних першого порядку від проекцій векторних полів у відповідній системі координат. Зауважимо, що достатньо знайти один електричний вектор, наприклад , або один магнітний вектор, наприклад,і скориставшись матеріальними рівняннями (табл. 2.1) можна отримати два останніх вектораі.