7.5 Явище повного внутрішнього відбиття.

Вважаємо, що обидва контактуючі середовища – діелектрики, причому перше середовище оптично більш щільне, ніж друге, тобто або. Визначимо умови, при яких буде відсутня заломлена хвиля, тобто має місцеповне відбиття.

З другого закону Снелліуса слідує, що кут заломлення для даного випадку більше кута падіння:

. (7.57)

Умову (7.57) відображає променева схема на рис. 7.10, а. Отже, при якомусь куті падіння , якийназивається граничним кутом внутрішнього відбиття (критичним кутом), виявиться, що кут – прямий (рис. 7.10, б). Заломлений промінь немов би ковзає вздовж межі розділу. Якщо прийняти в (7.57), дляотримаємо

. (7.58)

Якщо кут падіння більше критичного (), то з (7.57) слідує, що. А це означає, що якщо значення кута падіння лежать в межах, то заломлення променю немає; не існують дійсні значення кута заломлення. Відбувається повне відбиття (рис.7.10,в). Область визначення дійсних значень кута заломлення являється умова.

Отже, для виникнення повного відбиття необхідно виконання двох умов:

– друге середовище повинне бути оптично менш щільним ніж перше (або);

– кут падіння повинен бути більше критичного ().

7.6 Імпедансні граничні умови (умови Леонтовича).

На відміну від звичайних граничних умов (розділ 3), які зв'язують значення складових поля на межі розділу в різних середовищах, імпедансні умови виражають зв'язок між складовими векторів ів одному середовищі.

Вважаємо, що друге середовище оптично більш щільне, ніж перше, тобто . Згідно з другим законом Снелліуса

. (7.59)

Це означає, що при будь-якому куті падіння хвиля в другому середовищі розповсюджується практично по нормалі до межі розділу (рис. 7.11). Отже, в цьому випадку вектори напруженості поля паралельні межі і зв'язані умовою

. (7.60)

Це відношення справедливе для будь-якої точки другого середовища, в тому числі і для межі розділу. Оскільки нормальні складові дорівнюють нулю, а тангенціальні неперервні при переході через межу, можна зробити заміну виду на, ана.

З урахуванням цього зауваження з формули (7.60) слідує, що . Остаточно, при k₂ > k₁ для дотичних складових поля в першому середовищі має місце співвідношення

. (7.61)

де

(7.62)

і називається поверхневим імпедансом, який на межі розділу з оптично дуже щільним середовищем дорівнює її характеристичному опору. Рівність (7.61) була одержана М.А. Леонтовичем при дослідженні ним розповсюдження радіохвиль. Ця умова застосовується у випадку, якщо середовища які контактують, суттєво відрізняються по параметрам (наприклад, повітря – метал). При цьому не вимагається визначати електромагнітне поле в оптично щільному середовищі. Розв'язок зводиться до задачі для одного середовища з заданим імпедансом на її межі.

7.7 Повне відбиття і напрямлені хвилі.

При повному відбитті від межі розділу відбита хвиля несе таку ж енергію, як і падаюча. На рис. 7.12 показана векторна діаграма, на якій середні значення вектору Пойнтинга розкладені наі. З рисунку видно, що нормальні компоненти взаємно знищуються, а дотичні складаються, при цьому потік енергії переноситься вздовж межі. При цьому формується особливий хвильовий процес, спрямований межею розділу середовищ.

Розглянемо спочатку повне відбиття від ідеально провідної межі ,.

Перпендикулярна поляризація. З формул Френеля для цього виду поляризації (7.38) слідує, що в цьому випадку

. (7.63)

Поле в першому середовищі являється суперпозицією падаючої і відбитої хвиль (7.26):

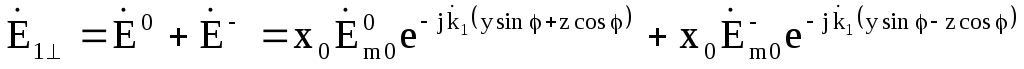. (7.64)

Через те, що відбиття повне, то , тоді

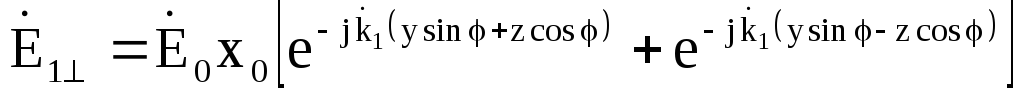. (7.65)

Перетворити вираз (7.65) можна, якщо звернутися до відомих тригонометричних тотожностей виду

В результаті одержимо:

. (7.65)

Якщо провести аналогічні операції з падаючою і відбитою хвилями для вектору магнітного поля (7.27), то отримаємо:

(7.67)

Паралельна поляризація. При з (7.45), маємо

. (7.68)

Результуюче поле для цього виду поляризації з урахуванням попереднього алгоритму перетворення для електричного і магнітного полів будуть мати вигляд:

(7.69)

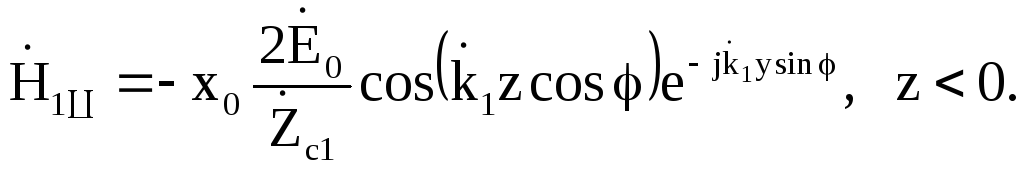(7.70)

Проаналізуємо вирази для полів (7.66) і (7.67), (7.69) і (7.70). Кожне з них має характер хвилі, яка розповсюджується в напрямку у, а в площинах фронту (у=const) – це стояча хвиля (площина рівних амплітуд). Через те, що площини цих хвиль не співпадають (вони взаємно перпендикулярні), то хвиля являє собою неоднорідну плоску хвилю. Вона відрізняється від раніше розглянутої плоскої хвилі в ізотропному однорідному середовищі тим, що має і повздовжні (паралельні напрямку розповсюдження) складові.

При перпендикулярній поляризації вектор лежить в поперечній площині, а вектормає дві складові: поперечнуі повздовжню(рис.7.15,а).

При паралельній поляризації, навпаки, вектор має дві складовіі, а векторлежить в поперечній площині(рис.7.15,б).

Процес характеризується двома хвильовими числами і, які зв'язані співвідношеннями:

(7.71)

Величина називаєтьсяповздовжнім хвильовим числом, або сталою розповсюдження, а –поперечним хвильовим числом. При дійсному :

(7.72)

де – фазова швидкість хвилі;

– просторовий період, тобто довжина хвилі вздовж розповсюдження;

– період стоячої хвилі в площині фронту.

Фазова швидкість неоднорідних хвиль вище, ніж у однорідних хвиль

(7.73)

Такі хвилі, у яких називаються“швидкими” хвилями. На відстанях від межі розділу лежать площини, на яких виконується гранична умова. Ці площини можна замінити ідеально провідними площинами без будь-якого порушення структури поля. Одержується найпростіший плоский порожній хвилевід.

Формально, поле в другому середовищі, уявимо як заломлену хвилю:

. (7.74)

Згідно з другим законом Снелліуса

(7.75)

При повному відбитті, підкореневий вираз в (7.75) від’ємний, тому – уявна величина:

(7.76)

Якщо підставити (7.76) в (7.75), то отримаємо

. (7.77)

Так як при віддаленні від поверхні розділу двох середовищ (при ) поле не може необмежено зростати, в показнику необхідно вибрати знак “мінус”. Тоді поле в другому середовищу експоненціально зменшується при віддаленні від межі розділу середовищ (рис.7.13). Таким чином, поле в другому середовищу –плоска неоднорідна хвиля, яка розповсюджується вздовж z. Так як поле зосереджене поблизу поверхні розділу, то таку хвилю називають поверхневою хвилею. В цьому випадку, при повному відбитті, , тому швидкість хвилі в другому середовищіменше

(7.78)

Такі хвилі називають ще ”повільними” хвилями на відміну від швидких хвиль, у яких в даному середовищі. Кут заломленняявляється комплексною величиною. Дійсна частина дорівнюєі показує напрямок розповсюдження хвилі, а уявна – швидкість зменшення амплітуди цієї хвилі вздовж осі z.

7.8 Плоскопаралельний хвилевід.

З розподілу компонент векторів поля (рис. 7.13) в площині фронту, раніше розглянутих неоднорідних хвиль ів (7.8) видно, що якщо ввести ряд площин, розміщених на відстанях

, (7.79)

від межі розділу, то для них будуть виконуватися умови . Це означає, що якщо будь-яку з цих площин замінити ідеально провідними площинами, то порушення структури поля не відбудеться. Таким чином, ми переходимо до напрямляючої системи, яка утворена двома паралельними ідеально провідними площинами. В середині такої системи можуть існувати попереднііхвилі. Утворюються найпростіший порожниний хвилевід.

Якщо зафіксувати відстань між пластинами (), то можна визначити поперечне хвильове число, скориставшись для цього виразом (7.72):

. (7.80)

З (7.79) визначаємо :

. (7.81)

Прирівнявши (7.80) і (7.81) визначимо :

, (7.82)

де n=0 має зміст тільки для горизонтальної поляризації (7.69) (7.70). Умова (7.82) показує, що для такого типу хвилеводу можливе існування безліч інших полів, крім розглянутих раніше іполів в 7.8. Послідовність значень поперечного хвильового числазадовольняє розв’язкам (7.66–7.67) і (7.69–7.70), а також граничним умовам. Змінюючиn можна отримати різні тапи хвиль. На рис. 7.14 зображені розподіли іскладових в площині фронту напрямляючої хвилі для вертикальної і горизонтальної поляризації.

Отримаємо важливі параметри, характеризуючі розповсюдження хвилі в порожнинному хвилеводі. З виразу (7.71) можна отримати вираз для повздовжнього хвильового числа.

. (7.83)

Тут k – хвильове число для необмеженого середовища з тими ж властивостями, що і середовище між площинами і воно дорівнює

. (7.84)

Виносячи k з під корення і враховуючи, що

,

приходимо до виразу

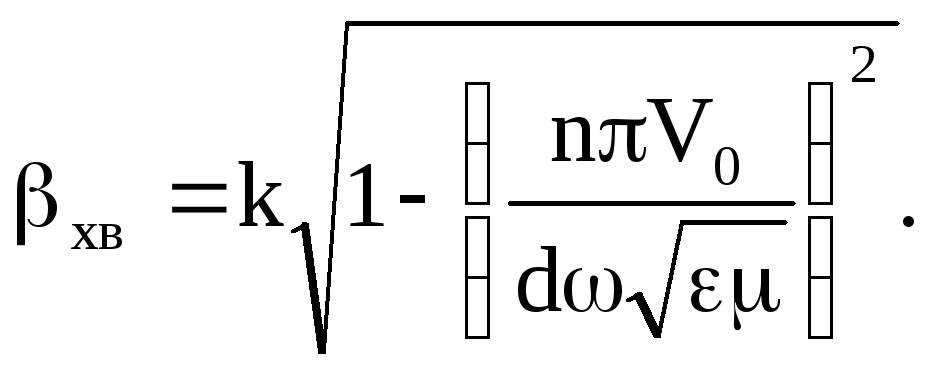
Введемо параметр , який називаєтьсякритичною частотою і яка дорівнює

. (7.85)

Остаточно, формула для повздовжнього хвильового числа буде мати вигляд з урахуванням (7.85):

(7.86)

Звідси знаходиться фазова швидкість і довжина напрямляючої хвилі . Виходячи з (7.72) для визначення:

,

маємо

; (7.87)

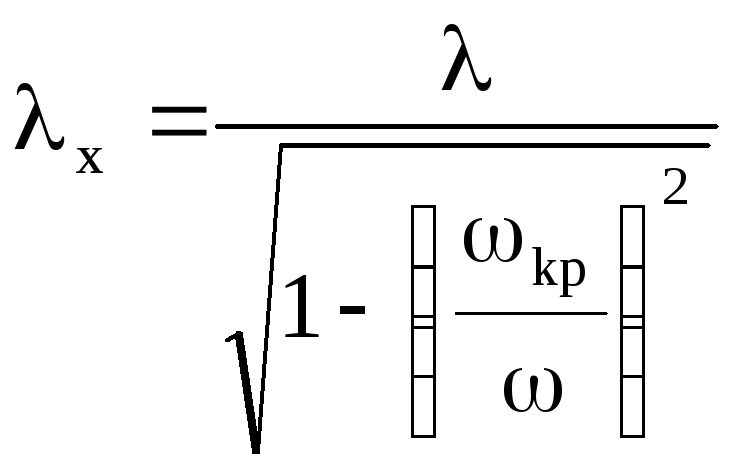. (7.88)

З виразу (7.87) і (7.88) видно, що ізалежать від частоти, тобто розповсюдження напрямлених хвиль супроводжується дисперсією.

Висновки.

1. Фазова швидкість і довжина хвилізавжди більше відповідних величин в необмеженому середовищі:

2. На частоті , яка дорівнює критичнійіперетворюються в нескінченність. При цьому поле між площинами вже не буде хвилею, яка розповсюджується. Поле стає синфазним, тобто енергія не переноситься. Це стояча хвиля. Хвиля нормально падає на межі, кут падіння.

3. Хвиля буде напрямленою, якщо . При цьомубуде дійсною величиною. Це означає, що фазовий набіг буде змінюватися за лінійним законом при зміні координати Y, що являється ознакою рухомої хвилі.

4. Якщо , тостає уявною величиною

,(7.89)

тобто поле зберігає сталу фазу і в напрямку розповсюдження Y буде зменшуватися за експоненціальним законом

(7.89 а)

Умова (7.89) ще називають “умовою відсікання”. Вона виконується, як правило, для вищих n. Чим менше n, тим нижче , приn=0 вона перетворюється в нуль. В цьому єдиному випадку буде розповсюджуватися плоска однорідна хвиля, у якої відсутня повздовжня складова.

Розповсюдження напрямляючих хвиль в плоскому хвилеводі можна легко пояснити за допомогою багатократного відбиття від площин (рис. 7.15). На основі (7.71) і порівнянні з (7.86) отримаємо:

. (7.90)

З рис. 7.15 видно, що при поступовому зменшенні кута падіння , зменшується частотадо. При кутах падіння близьких до 90^о, хвилі, відбиваючись від площин, розповсюджуються рівномірно, що можливо при високих частотах . Із зменшенням частоти, збільшується, тобто кутзменшується, а при,. При цьому хвиля розповсюджується нормально до площин хвилеводу. Енергія передаватися по хвилеводу не буде. Таким чином, хвиліітипу можуть формуватися на досить високих частотах (до). На низькихї частотах формується хвиля ТЕМ.