Характеристичний опір

, (6.58)

якщо =1, то

. (6.59)

Реальні діелектрики характеризуються надто малими кутами втрат порядку 10^-4, 10^-3, тоді можна вважати, що кут . Тобто векториісинфазні.

На рис. 6.4 наведена залежність миттєвих значень івід координати z в деякий фіксований момент часу t=t₀ для даного середовища.

Розповсюдження плоских хвиль в провідниках (металі). В провідниках:

.

Згідно зробленому допущенню комплексну діелектричну проникність металоподібного середовища можна вважати уявною.

. (6.60)

Тоді коефіцієнт розповсюдження для даного середовища буде визначатися виразом

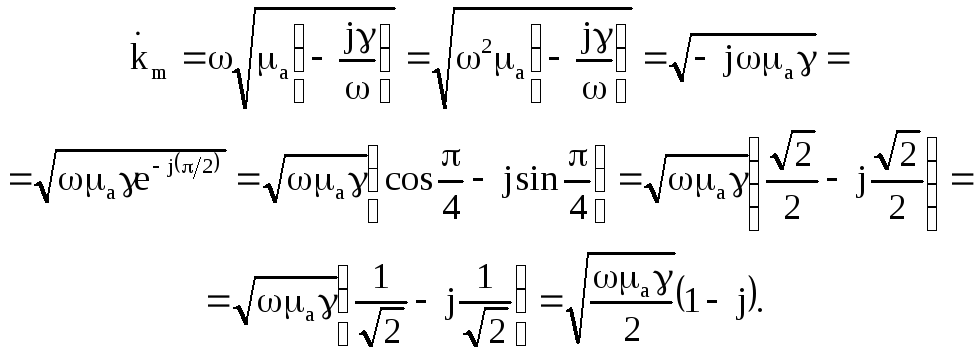
Отже

(6.61)

Для металів справедлива рівність

(6.62)

Фазова швидкість

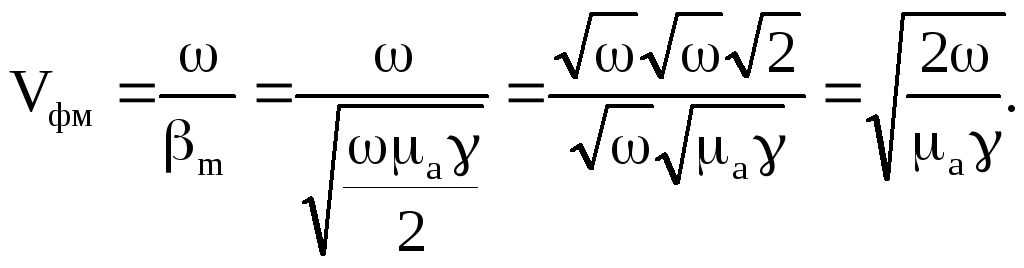(6.63)

Групова швидкість

(6.64)

тобто

(6.65)

Характеристичний опір

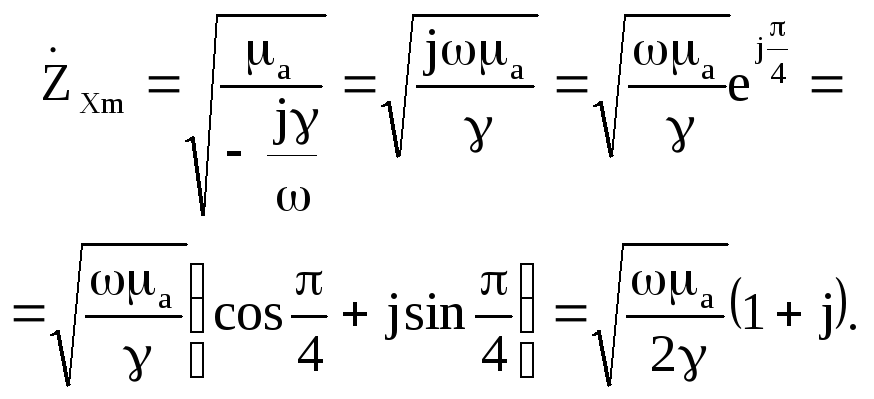(6.66)

З (6.66) видно, що із збільшенням , модульзменшується, і в даному середовищі виявляється рівним нулю

(6.67)

Це говорить, що в провіднику переважне значення має магнітне поле. Між векторами ііснує зсув фаз, рівний, то середнє значення вектору Пойнтинга для миттєвих значень

Але

тому

В ідеально провідному металі коефіцієнт затухання хвилі, що розповсюджується – велика величина. Тому її амплітуда різко зменшується, тобто вона в напрямку розповсюдження швидко затухає.

Нехай амплітуда напруженості електричного поля з координатою z дорівнює , а в точці з координатою z+l дорівнює. Відношення

(6.68)

показує в скільки раз зменшується амплітуда хвиль при проходженні нею відстані l.

Затухання вимірюють в неперах і децибелах. Затухання в неперах визначається як натуральний логарифм відношення (6.68)

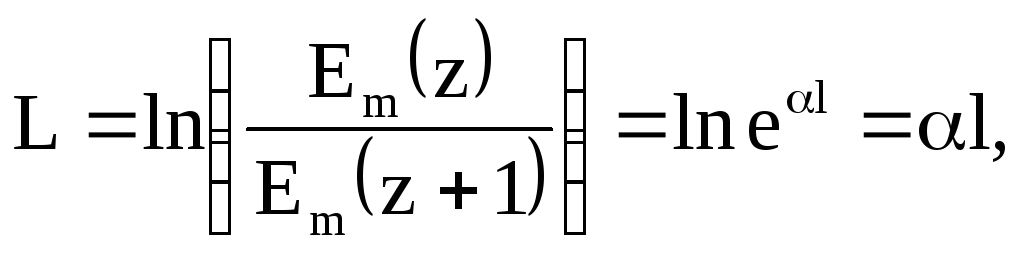неп.

Затухання в децибелах

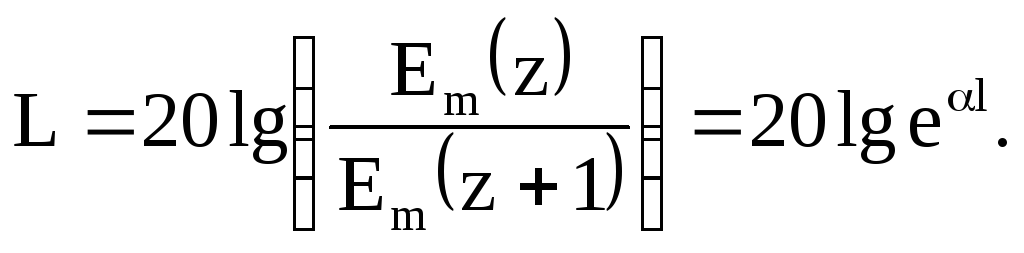
Використовуючи модуль переходу від натурального логарифма до логарифму за будь-якою основою

остаточно отримуємо затухання в децибелах:

дБ, (6.69)

тобто 1 дБ = 8.69 неп.

Коефіцієнт визначає затухання хвилі при проходженні нею шляху в один метр і вимірюється в неперах на метр (неп./м.)

В наслідок великих теплових втрат (велика величина ) електромагнітне поле в провіднику швидко затухає. Це призводить до того, що струм високої частоти, проходячи по провіднику, зосереджується безпосередньо у його поверхні. Це явище називається поверхневим ефектом або скін-ефектом. Для характеристики скін-ефекту вводиться поняття глибини проникнення поля в середовище (рис. 6.5). Глибина проникнення поля в середовище – це відстань, при проходженні якого електромагнітне поле послаблюється в е=2.718 раз:

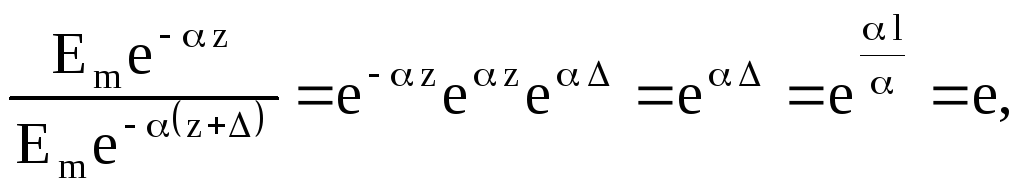
тобто

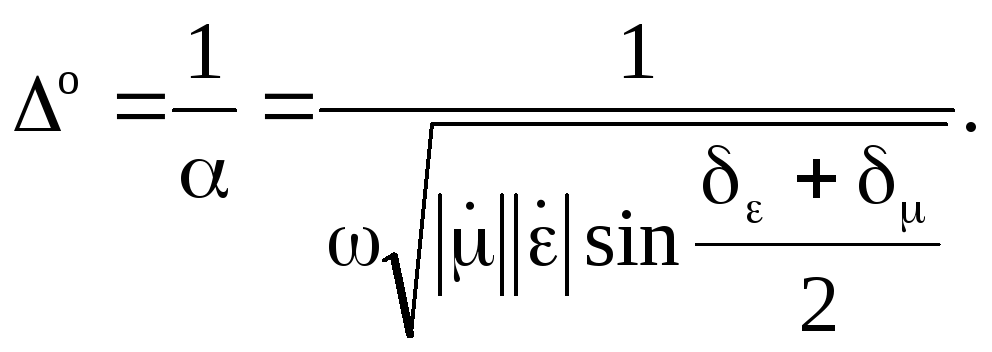(6.70)

У випадку металу формула (6.70) спрощується

(6.71)

З (6.70) видно, що залежить від частоти; чим більше частота, тим менш. Розрахунок по (6.71) показує, що для металів на частотах НВЧ діапазону,виявляється надто малою. Так, для міді на f=10 ГГц,=5.7 10⁷ , маємо=0.6 мкм. Це використовується на практиці: наноситься шар добре провідного металу, наприклад, срібла, на поверхню виробу, що зменшує теплові втрати (близько 0.01 мм).

6.3 Поляризація електромагнітних хвиль.

Електромагнітна хвиля має векторний характер. Для її повної характеристики необхідно крім амплітуди, фази і частоти вказати поляризацію хвилі, тобто напрямлення векторів ів просторі. Для плоскої хвилі треба знати напрямок векторівів площині хвильового фронту за період коливання. Взявши за основу падаючу хвилю, визначимо можливі випадки поляризації плоских хвиль.

З виразів (6.14) і (6.15) запишемо ікомпоненти падаючої хвилі:

(6.72)

Сталі і– комплексні величини, тобто

(6.73)

В середовищі з втратами – величина комплексна, тому складовіізапишуться у вигляді

(6.74)

Перейдемо від комплексів до миттєвих значень:

(6.75)

(6.76)

Введемо позначення:

(6.77)

Тоді розділивши (6.75) на , а (6.76) наі скориставшись позначення (6.77), отримаємо

(6.78)

(6.79)

Визначимо з (6.78) співмножник :

(6.80)

Перетворимо (6.79) до більш зручного вигляду, застосувавши до множника відоме тригонометричне співвідношення вигляду. Тоді (6.79) буде мати вигляд:

(6.81)

Подальше перетворення полягають в наступному:

(6.82)

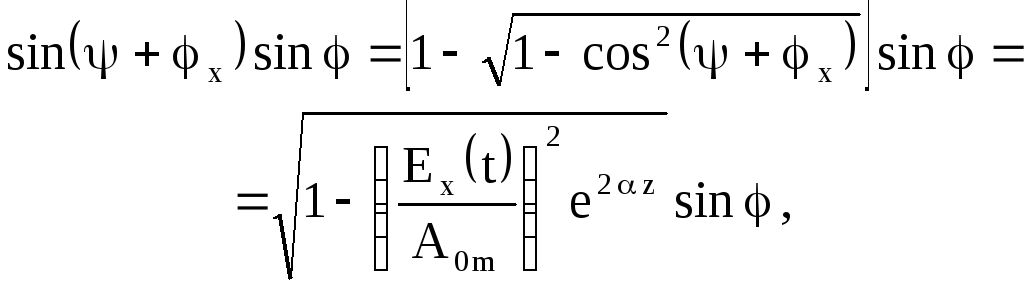(6.83)

З урахуванням (6.82) і (6.83) вираз (6.81) приймає вигляд:

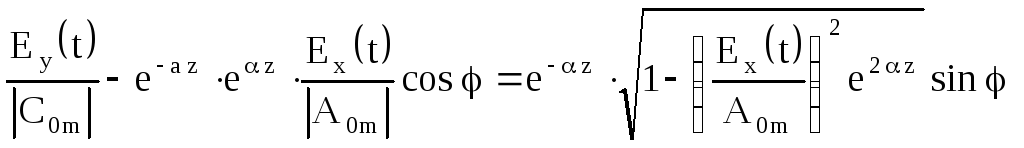, (6.84)

або підводячи до квадрату обидві частини цієї рівності і виконавши нескладні перетворення, отримаємо

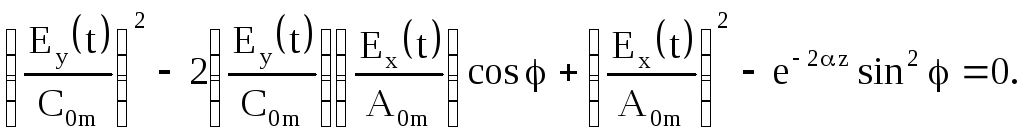(6.85)

Складові івектора напруженості електричного поля можна розглядати як координати кінця векторана площині x y. Положення цього вектора визначає характерполяризації поля. Спростимо запис (6.85), зробивши слідуючи заміни

(6.86)

Тоді (6.85) запишеться у вигляді

(6.87)

Отриманий вираз являється рівнянням кривої другого порядку в координатах і. Таким чином, в загальному випадку кінець векторапереміщується по кривій другого порядку. В аналітичній геометрії показано, що характер цієї кривої визначається знаком детермінанту:

(6.88)

Якщо детермінант більше нуля , то крива представляє собоюеліпс, в конкретному випадку коло. Якщо детермінант дорівнює нулю , еліпс вироджується впряму лінію.

Покажемо, що в залежності від співвідношення амплітуд іі початкових фазіможна отримати різні види поляризації.

А. Еліптична поляризація. При довільних іі різниці початкових фазрівняння (6.85) представляє собою рівняння еліпса, який розташовується в площині XOY і вписаного в прямокутник з сторонамиі(рис. 6.6) при фіксованому z і змінному t. Кінець векторапереміщується по еліпсу з кутовою швидкістю, виникає еліптична поляризація. В момент часугеометричним місцем точок кінця вектораявляється гвинтова лінія (спіраль) з крокомна поверхніеліптичного циліндра (рис. 6.7). З плином часу гвинтова лінія, яка визначає орієнтацію вектора переміщується вздовж z з швидкістю.

В загальному випадку при довільному співвідношенні між початковими фазами, рівняння (6.85) представляє собою еліпс, велика вісь якого нахилена під деяким кутом до осі OX (рис. 6.8):

(6.89)

де .

Для визначення степені еліптичності, вводять коефіцієнт еліптичності, якій дорівнює

(6.90)

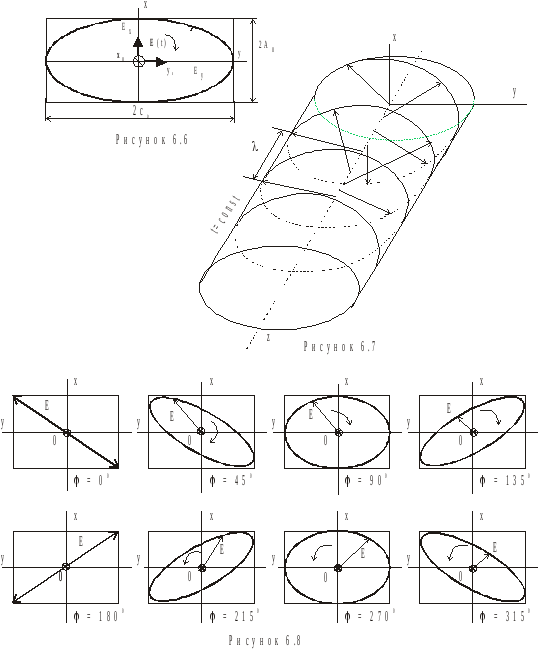
При отримуємо лінійну поляризацію;– кругову поляризацію. Таким чином, еліптично поляризована хвиля включає в себе хвилю лінійно поляризовану і хвилю з кутовою поляризацією. З рис. 6.8 видно, що приі(випадок синфазності або противофазності складових) еліптична поляризація вироджується в лінійну. Орієнтація площини поляризації залежить від співвідношення міжі(рис. 6.8), в поглинаючих середовищах, розміри еліпса при русі вздовж z зменшуються (рис. 6.7).

Б. Кругова поляризація. В цьому випадку амплітуди складових ірівні, а їх початкові фази відрізняються на. Рівняння (6.85) запишеться у вигляді

(6.91)

В середовищі без втрат , тоді рівняння (6.91) приймає вигляд

(6.92)

Це рівняння представляє собою рівняння кола з сталим радіусом. Виникає кругова поляризація. Кінець вектора обертається при зміні часу і z по колу. Геометричним місцем точок кінця вектораприявляється гвинтова лінія на поверхнікругового циліндра.

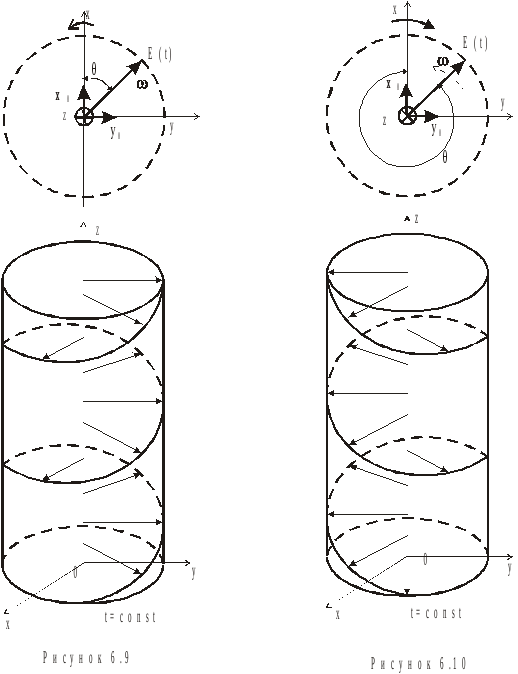
В залежності від напрямку обертання вектора розрізняють хвилі зправою і лівою круговою поляризацією (рис. 6.9, 6.10). складові ів цьому випадку визначаються виразами:

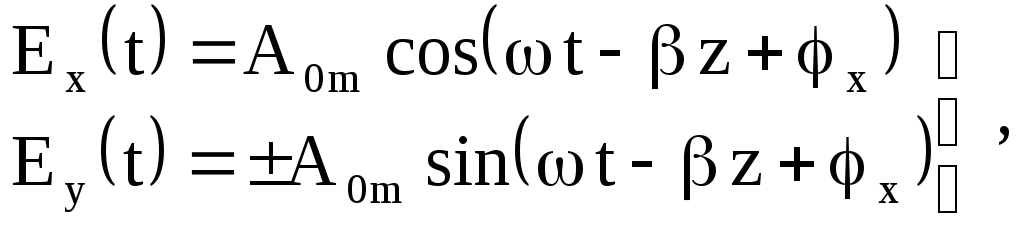(6.93)

так як .

Величина вектора при цьому залишається незмінною:

Кут (рис. 6.9) між віссюx і вектором в фіксованій точці простору (z) визначається співвідношенням

(6.94)

З виразу (6.94) видно, що в кожній фіксованій точці спостереження , кутлінійно зростає по законуіз збільшенням, змінюючись наза час одного періоду.

Лівогвинтова поляризація: . При такій умові складовібуде відставати відна кут. Результуючий векторв точцірівномірно обертається з кутовою швидкістюв напрямку віддо(за часовою стрілкою, якщо дивитися в напрямку), тобто в сторону складової, яка відстає по фазі; кінець вектора описує коло (рис. 6.8, а).

Але з (6.94) слідує також, що в кожний фіксований момент часу кутлінійно зменшується за закономіз збільшенням координати, змінюючись нана відстані рівній. Отже, привекторрівномірно повертається із збільшенням координатив напрямку віддо(проти часової стрілки, якщо дивитися вздовж напрямку розповсюдження хвилі), роблячи один оберт на відстані. Кінці векторів, які відносяться до різних точок на осі Oz розташовані при цьому налівогвинтовій круговій спіралі (рис. 6.8, б).

Правогвинтова поляризація: . В цьому випадку складовабуде випереджатина кут. Зробивши аналогічні роздуми, що і для попереднього випадку, отримаємо, що привекторобертається з кутовою швидкістюпроти часової стрілки, тобто. віддо(рис. 6.9, а). А в момент часу, векторрівномірно повертається із збільшенням координатив напрямку віддо(за часовою стрілкою, якщо дивитися вздовж напрямку розповсюдження хвилі). Кінці векторіврозташовані направогвинтовій круговій спіралі (рис. 6.9, б).

В. Лінійна поляризація. Якщо в рівнянні (6.85) , то його можна записати у вигляді

або

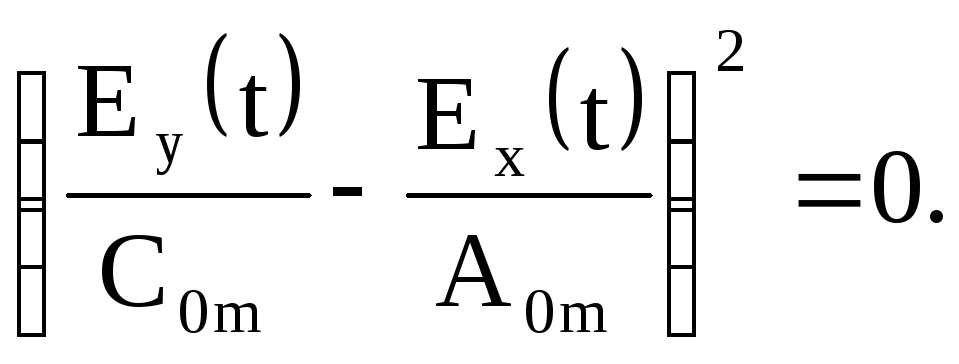
Звідки

(6.95)

Рівняння (6.95) являється рівнянням прямої лінії, нахил якої до осей визначається кутовим коефіцієнтом :

(6.96)

З цього виразу видно, що кут сталий і не змінюється за часом. В загальному випадку кутможе змінюватися за часом. Отже, векторв будь-який момент часу лежить в площині, яка проходить через вісьі складає кутз площиною ХОZ (рис. 6.9, а), якщоі т.д. і, якщоі т.д. (рис. 6.9, б). Векторзберігає свою орієнтацію незміною, але його миттєве значення змінюється за часом з частотою. Таким чином, результуюча хвиля буделінійно-поляризована.

Очевидно, що повертанням осей координат івідносно осіможна досягнути того, щоб векторв новій системі координат мав тільки одну складовуабо(рис. 6.9, в). Будь-яку лінійно-поляризовану хвилю можна представити у вигляді суми двох хвиль з круговою поляризацією.

Нехай лінійно-поляризована хвиля розповсюджуються в напрямку осі і має вектор паралельний осі ОХ:

(6.97)

Додамо і віднімемо в правій частині в (6.95) вираз

отримаємо

(6.98)

Перша квадратна дужка в (6.96) – хвиля з правою круговою поляризацією, а друга – хвиля з лівою круговою поляризацією (рис. 6.10). Результуючий вектор в два рази перевищує амплітуду доданків, поляризованих по кругу.

При визначені поляризації хвилі розглядався тільки вектор . Очевидно, що такий же аналіз можна зробити і для вектора. В загальному випадку кінець векторав фіксованій точці простору з плином часу також описує еліпс, подібний еліпсу вектораі повернутий відносно нього на кут(рис. 6.11).