6 Плоскі електромагнітні хвилі

6.1 Загальні властивості плоских електромагнітних хвиль.

В рівняння Гельмгольца (5.14), (5.15) вектори івходять однаковим чином. Тому повинні бути однаковими розв’язки цих рівнянь. Векториізв’язані рівняннями Максвела, то достатньо розв’язати одне з рівнянь Гельмгольца. Розв’язком являється функція координат і часу. Вона описує електромагнітні хвилі, які розповсюджуються в вільному просторі, в хвилеводах, об’ємних резонаторах і інших пристроях.

Хвильові гармонійні процеси характеризуються амплітудою, частотою (періодом) і фазою. Фаза коливань визначається не тільки часом t, але і відстанню від джерела хвиль до точки спостереження z, і швидкістю розповсюдження електромагнітних коливань :

,

де – фаза хвильового процесу;

– початкова фаза;

V – швидкість розповсюдження електромагнітних коливань.

Крім фази, швидкості розповсюдження, електромагнітні хвилі характеризуються довжиною, формою хвильової поверхні і поляризацією. Фазовим фронтом (хвильовою поверхнею) називається поверхня, в усіх точках якої основні вектори поля імають однакову фазу, інакше кажучи, на поверхні коливання синфазні.

В залежності від форми фазового фронту хвилі можуть бути плоскими, циліндричними, сферичними і мати більш складну форму хвильової поверхні.

Фазова швидкість - швидкість переміщення фазового фронту.

Довжина хвилі - відстань в напрямку розповсюдження електромагнітних коливань, на якій, при фіксованому моменті часу, фаза цих коливань змінюється на .

Розглянемо найважливіші властивості електромагнітних хвиль на найпростішому прикладі плоскої однорідної хвилі, яка розповсюджується вздовж вісі z в однорідному ізотропному середовищі.

У плоскої хвилі эквіфазна поверхня представляє собою площину (z=const). Хвиля називається однорідної, якщо її амплітуда стала в усіх точках фазового фронту тобто не залежить від координат цієї площини і неоднорідною, якщо її амплітуда залежить від координат точок фазового фронту.

Аналіз однорідної плоскої хвилі будемо проводити в декартовій системі координат. Її поле за визначенням не залежить від координат x і y, отже, хвиля характеризується співвідношенням

. (6.1)

Запишемо при цих умовах перші два рівняння Максвела в координатній формі

, (6.2)

, (6.3)

, (6.4)

, (6.5)

, (6.6)

. (6.7)

З виразів (6.4) і (6.7) слідує, що повздовжні складові поля ідорівнюють нулю, тобто електромагнітне поле має тільки поперечні складові (компоненти)тобто, а. Отже, векториілежать в площині, перпендикулярній напрямку розповсюдження z. Така хвиля називаєтьсяпоперечною електромагнітною хвилею, або ТЕМ, або згідно з ДСТУ Т-хвилею.

Рівняння (6.2-6.6), що залишалися, діляться на дві групи:

. (6.8)

. 6.9)

Ці дві системи можна розв’язати незалежно один від одного .

Продиференцюємо, наприклад, (6.6) по z; з урахуванням (6.2) отримаємо

. (6.10)

Рівняння (6.10) представляє собою однорідне рівняння Гельмгольца.

Параметр в загальному випадку комплексна величина

(6.11)

і називається хвильовим числом.

Через те, що рівняння (6.10) залежить від однієї координати z, перпендикулярної плоским хвильовим поверхням, то в (6.10) частинні похідні замінимо повними

. (6.13)

Диференційне рівняння (6.13) другого порядку для має розв’язок у вигляді суперпозиції двох частинних розв’язків виду

, (6.14)

де – довільні сталі інтегрування, які представляють собою комплексні амплітуди, наприклад,; які визначаються з граничних умов. Підставивши розв’язок (6.14) в (6.6), отримаємо

, (6.15)

звідки

,

або

. (6.16)

Враховуючи, що , тоді (6.16) приймає вигляд

, (6.17)

де

. (6.18)

Величина вимірюється в омах і називаєтьсяхарактеристичним опором середовища. В загальному випадку величина комплексна. В середовищі без втратвеличина дійсна:

. (6.19)

Для вакууму ,

. (6.20)

Аналогічно виконавши операції, зроблені для , можна отримати розв’язок для.з (6.9) буде дорівнювати

, (6.21)

а , використовуючи (6.21) і (6.9) буде дорівнювати

. (6.22)

В середовищі без втрат (), стала розповсюдження - величина дійсна, тоді переходячи від комплексних амплітуд до миттєвих значень, знайдемо

(6.23)

де .

Вираз (6.23) описує плоску електромагнітну хвилю, причому – її амплітуда, а аргумент косинуса – повна фазазмінюється в часі і просторі, а отже, змінюється і положення фазового фронту. Залежність Ex від z в фіксований моменти часутазображена на рис. 6.1

Знайдемо швидкість переміщення фронту хвилі, для чого зафіксуємо фазу поля і. Продиференціювавши ці рівності за часом, отримаємо

.

Звідси фазова швидкість

і . (6.24)

Таким чином, складова представляє собою суперпозицію двох незалежних одна від одної рухомих хвиль, одна з якихрозповсюджується в напрямку зростаючих значень z з фазовою швидкістю, і називаєтьсяпадаючю, а інша – в напрямку зменшення значень z зі швидкістю – і називаєтьсявідбитою.

Рисунок 6.1

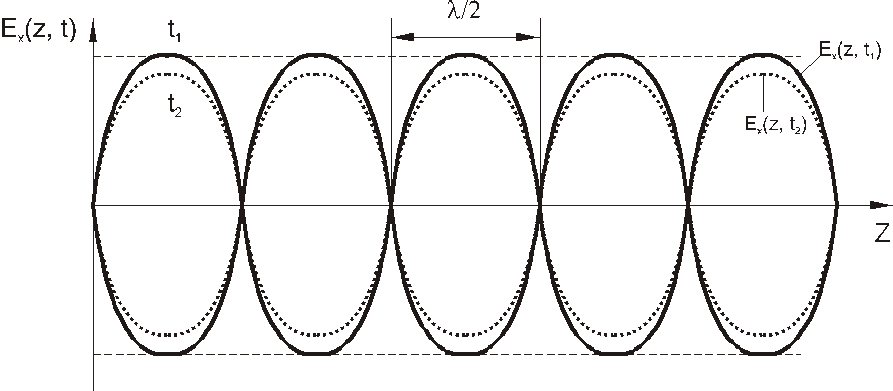
Рисунок 6.2

Поки що, будемо розглядати тільки падаючу хвилю, тому можна записати, опускаючи знак “+”, що

. (6.25)

Для вакууму

–швидкість світла. (6.27)

З (6.25) слідує співвідношення, яке зв’язує хвильове число та частоту у вільному просторі

, (6.28)

враховуючи, що .

Вираз (6.28), називається сталою розповсюдження електромагнітної хвилі у вільному просторі .

Використовуючи форму запису (6.23) переходу від комплексних амплітуд до миттєвих значень складової , можна представити інші компоненти поляу вигляді

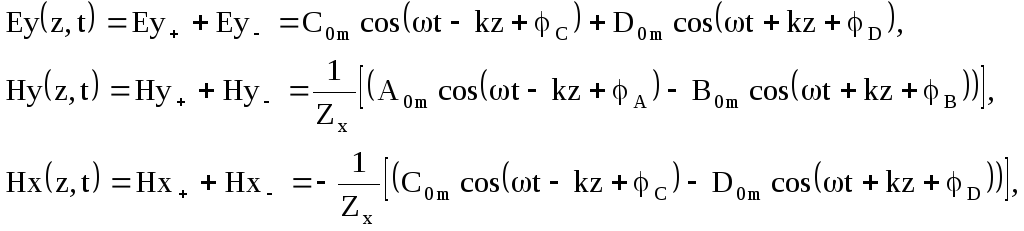(6.29)

. (6.30)

Отже, електромагнітне поле (6.23) і (6.29) представляє собою суперпозицію чотирьох незалежних рухомих хвиль, які визначаються і,і,і,і. Однорідні плоскі рухомі хвилі (6.23) і (6.29) розповсюджуються вздовж осі z, яка перпендикулярна їхнім хвильовим площинам. Згідно з (6.30) векториіцих хвиль лежать в хвильових площинах і представляють собою поперечні складові векторів поля по відношенню до напрямку розповсюдження.

Якщо, зокрема, амплітуда падаючої і відбитої хвиль рівні одна одній і дорівнюють початковій фази, то отримуємо стоячу хвилю. Наприклад, для складової:

,

використовуючи відому тригонометричну тотожність

,

отримуємо

. (6.31)

Як видно (рис. 6.3) в кожний момент часу маємо нерухому косинусоїду: її нулі не зміщуються вздовж осі z, а залишаються фіксованими. Отже, все сказане можна стисло записати рівняннями, які зв’язують компоненти поля плоскої хвилі, для середовища з втратами

, (6.32)

. (6.33)

Розповсюдження хвилі супроводжується переносом потужності. Комплексний вектор Пойнтинга має тільки дійсну частину

, (6.34)

де

. (6.35)

При довільному напрямку розповсюдження електромагнітної хвилі вздовж r, розв’язок рівняння Гемгольца можна записати

, (6.36)

де – радіус-вектор довільної точки спостереження;

– хвильовий вектор, перпендикулярний до хвильового фронту.