61

Максимальная погрешность (2.73) получается при сравнимых величинах _нр и _нэ (_нр  _нэ). При этом происходит более сильный спад АЧХ и Быстрый рост фазового сдвига (см. рис. 1.3 и 1.4).

Коэффициент усиления по току . Нормированная АЧХ и ФЧХ будут такие же, как в (2.64) и (2.65), следовательно, анализ производится так же.

2.5.4. Область высших частот

Снижение коэффициентов усиления в этой области частот (правее области средних частот на рис. 1.3) обусловлено зависимостью параметров транзистора от частоты и влиянием реактивных элементов внешних цепей (емкости монтажа и нагрузки, комплексной нагрузки и др.).

Наибольшее влияние на частотную характеристику (на частотные искажения) оказывают частотно-зависимый коэффициент усиления тока базы и барьерная емкость коллекторного перехода .

Частотная зависимость коэффициента обусловлена диффузионным характером движения носителей тока в базе и рассмотрена в разделе «Транзистор», где получена формула зависимости β от частоты:

.

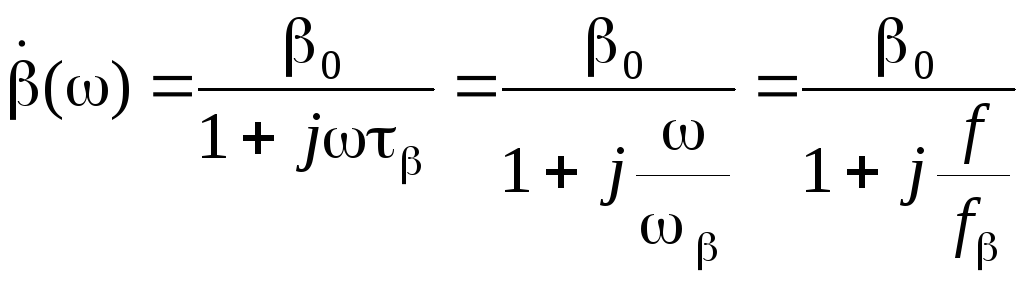Частотная зависимость характеризуется постоянной времени τ_β или граничной частотой f_β (или ) в схеме ОЭ. В свою очередь, τ_β, f_β, ω_β являются производными от граничной частоты (паспортного параметра) в схеме ОБ – f_α, (или ω_α) или τ_α:

, , , .

Барьерная емкость включена параллельно генератору тока и дифференциальному сопротивлению коллекторного перехода . С увеличением частоты уменьшается комплексное сопротивление параллельной цепи из и и увеличивается ответвляющийся в нее ток генератора тока , что ведет к уменьшению тока i_к во внешней цепи, т.е. к уменьшению коэффициента усиления каскада. Сами и становятся комплексными, т.к. они зависят от :

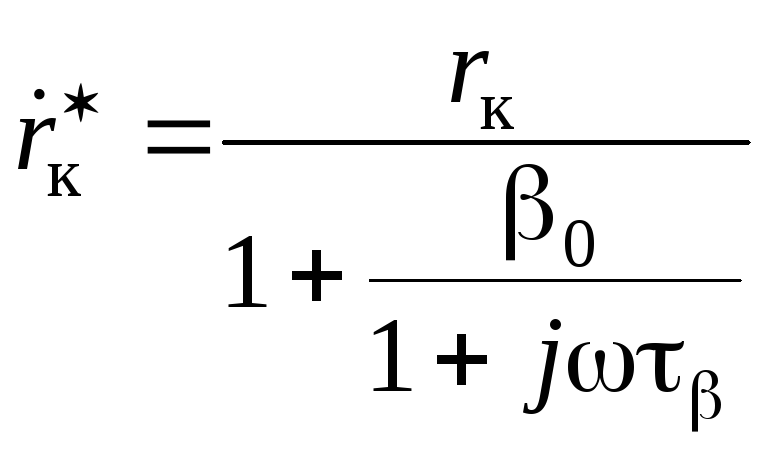, , (2.74)

В (2.74) β₀ – обыкновенная, не эквивалентная.

Все параметры каскада, зависящие от ,, , становятся комплексными (частотно-зависимыми). Это – входное сопротивление Z_вх (вместо R_вх), выходное сопротивление транзистора Z_i (вместо R_i ≈), коэффициенты усиления по току и напряжению .

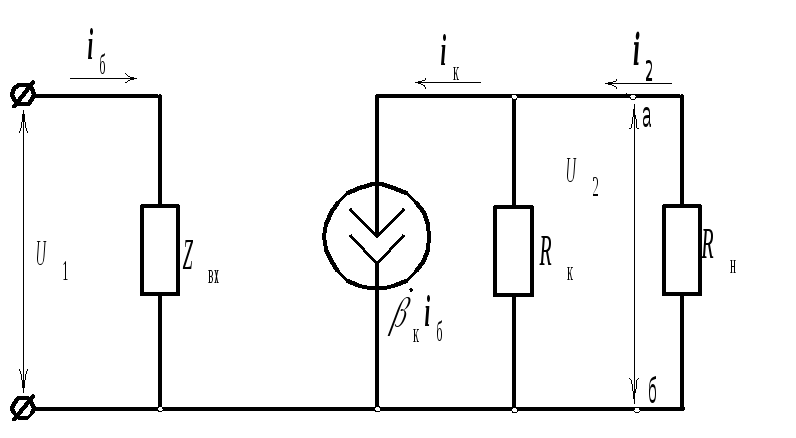
Н а рис. 2.11,а приведена эквивалентная схема каскада в области высших частот с учетом всех перечисленных выше условий.

а в

б

Рис. 2.11

Анализ этой схемы в общем виде, с учетом всех частотно-зависимых (комплексных) элементов приводит к появлению дополнительных полюсов и нулей в частотной характеристике и делает анализ весьма сложным. Для упрощения анализа вначале, как правило, вводят ряд ограничений, наиболее результативными из которых являются два:

1. Одиночный каскад. Прежде всего принимают, что внешние цепи каскада содержат только активные элементы (резисторы), вследствие чего частотные искажения (снижение коэффициентов усиления) обусловливаются только частотно-зависимыми параметрами транзистора. Это означает, что сначала анализируется одиночный (не промежуточный) каскад с активной нагрузкой R_н на выходе. Затем, с учетом полученных результатов, рассматривается промежуточный каскад с комплексной нагрузкой на выходе [6], каковой является входное сопротивление следующего каскада Z_{вх.след}.

2. Эквивалентный коэффициент . Влияние обоих, указанных ранее, частотно-зависимых параметров транзистора ( и ) на частотную характеристику сводят к одному эквивалентному коэффициенту усиления тока базы (или ) с эквивалентной постоянной (или эквивалентной граничной частотой ) [1,6]:

, , (2.75)

где β_0к – низкочастотный эквивалентный коэффициент из (2.43), γ_к – из (2.44),

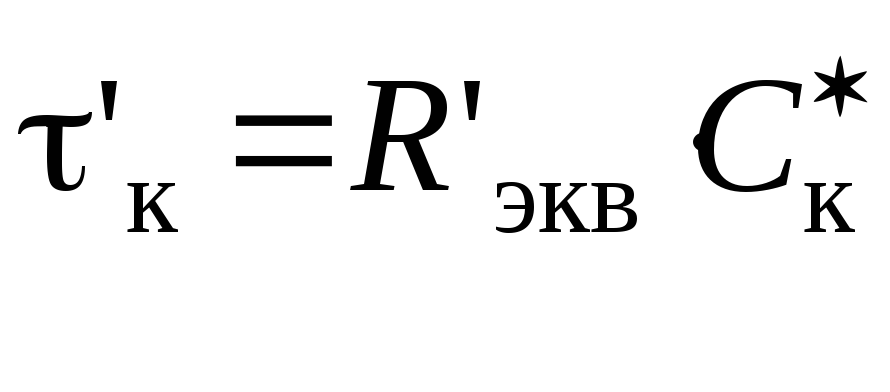, (2.76)

R'_экв – из (2.54).

Первое слагаемое τ_β∙γ_к в (2.75) отражает «вклад» коэффициента , а второе слагаемое τ_к – «вклад» барьерной емкости в эквивалентную постоянную τ_βк.

Эквивалентные и τ_βк в (2.75) легко могут быть получены, если внешний ток i_к (см. рис. 2.11,а) принять за ток эквивалентного генератора и определить его долю в токе исходного генератора с учетом шунтирующих элементов:

, , (2.77)

где 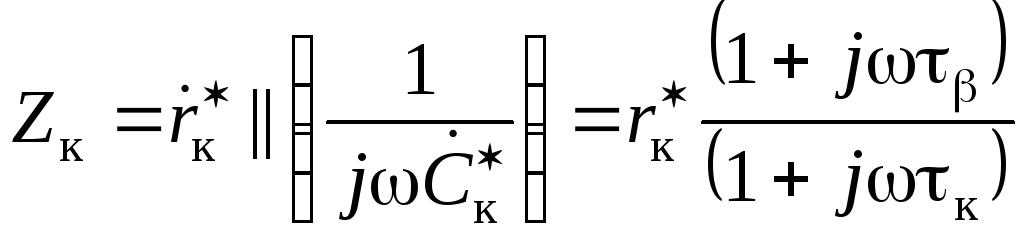, (2.78)

.

Подставив Z_к из (2.78) в (2.77), после несложных преобразований можно найти

,

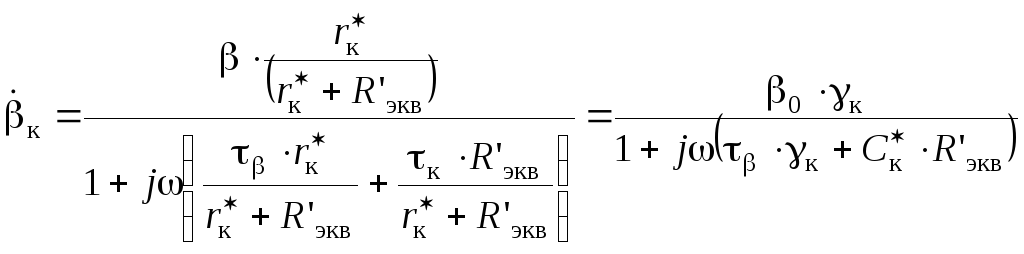что соответствует (2.75).

На рис. 2.11,б приведена эквивалентная схема с учетом введенных эквивалентных параметров и τ_βк с активной нагрузкой R_н. На этой схеме уже нет и , а R_i = ∞.

Параметры каскада в области высших частот определяются с учетом введенных эквивалентных и τ_βк по схеме на рис. 2.11,б.

Входное сопротивление Z_вх.

При источнике ЭДС на входе (R_г = 0)

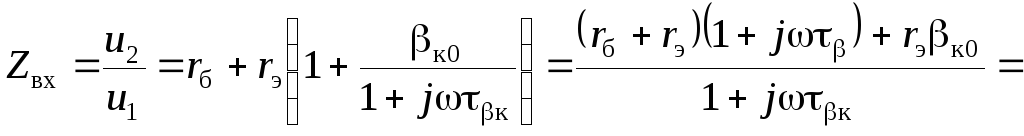
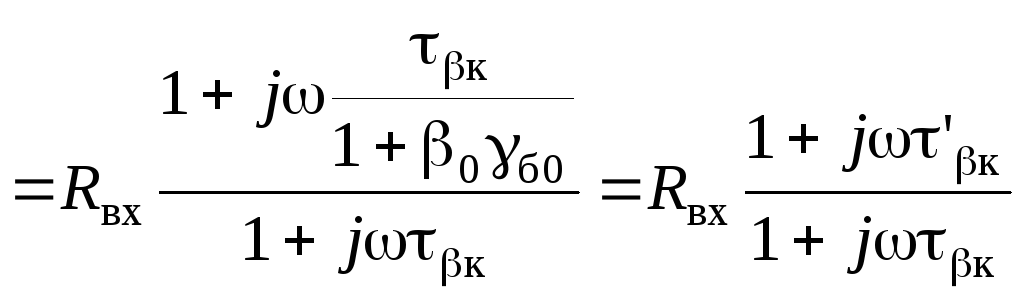, (2.79)

где R_вх, γ_б0 – из (2.45), τ_βк – из (2.76).

Как уже указывалось, почти всегда R_г > 0, поэтому вместо частного коэффициента γ_б0 нужно использовать общий коэффициент γ_б из (2.47). Тогда

. (2.80)

Коэффициент усиления по напряжению .

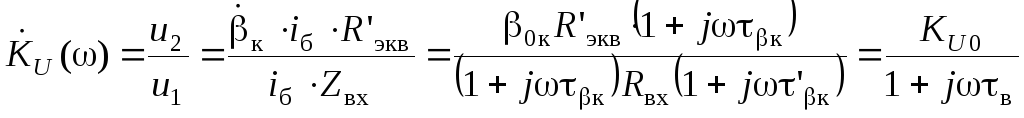, (2.81)

где

(2.82)

– постоянная коэффициента усиления в области высших частот.

Постоянная может значительно изменяться при разных величинах :

,

. (2.83)

Так для коэффициента усиления по току (= ∞ , γ_б = 0) :

. (2.84)

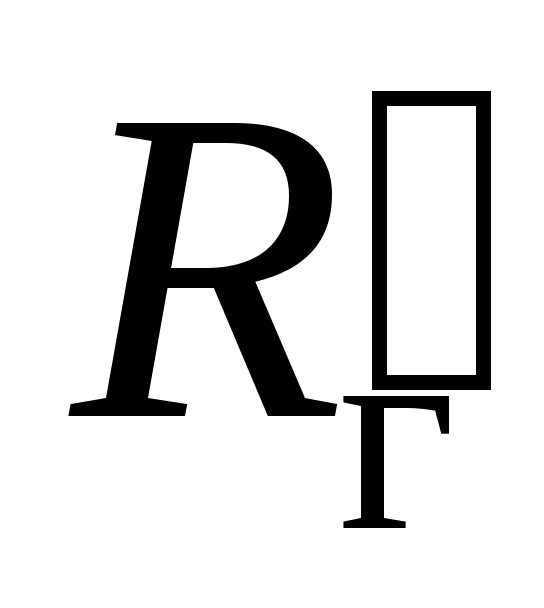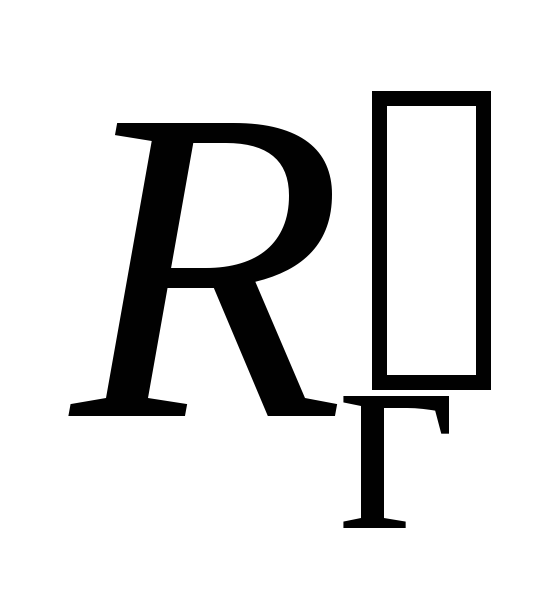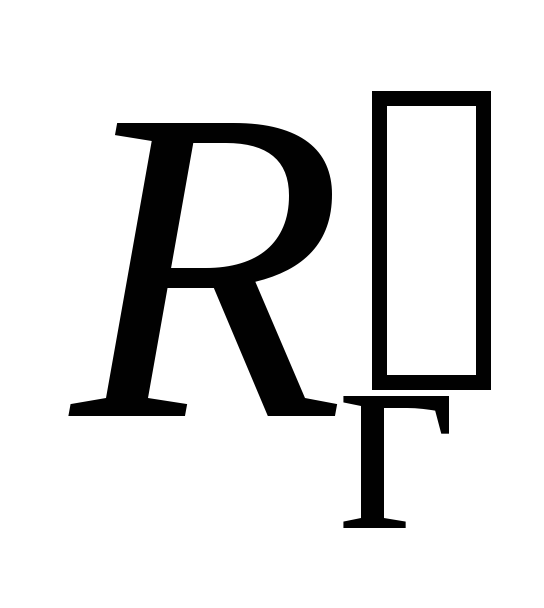
Таким образом, в зависимости от величины может значительно изменяться высшая граничная частота f_в каскада: при = ∞ она наименьшая, при  0 она значительно больше (в 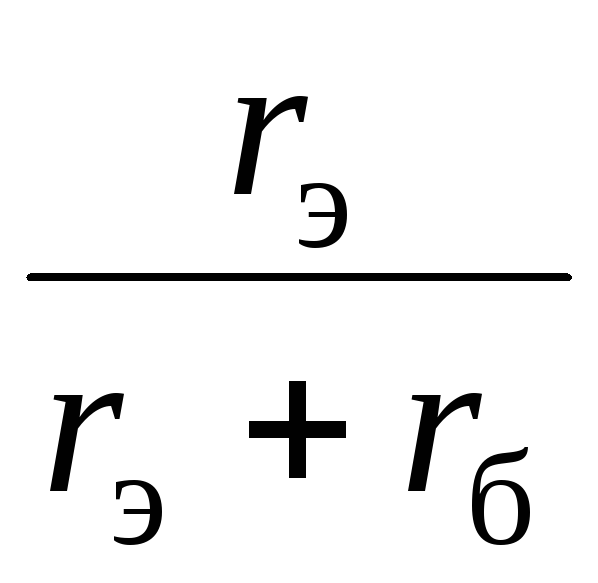раз).

В комплексных выражениях (2.81) и (2.84) содержатся АЧХ:

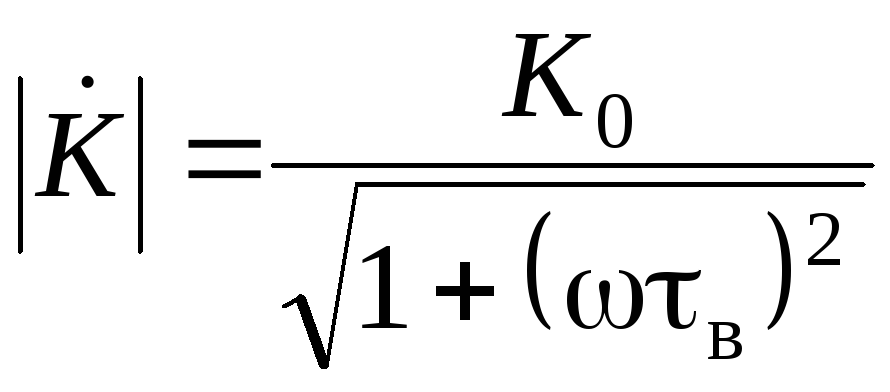, (2.85)

и ФЧХ в радианах:

. (2.86)

На практике вместо (2.85) удобнее использовать нормированную АЧХ:

. (2.87)

Уровень частотных искажений в области высших частот (как и в области низших) задается одной точкой на нормированной АЧХ с координатами М_в, f_в ():

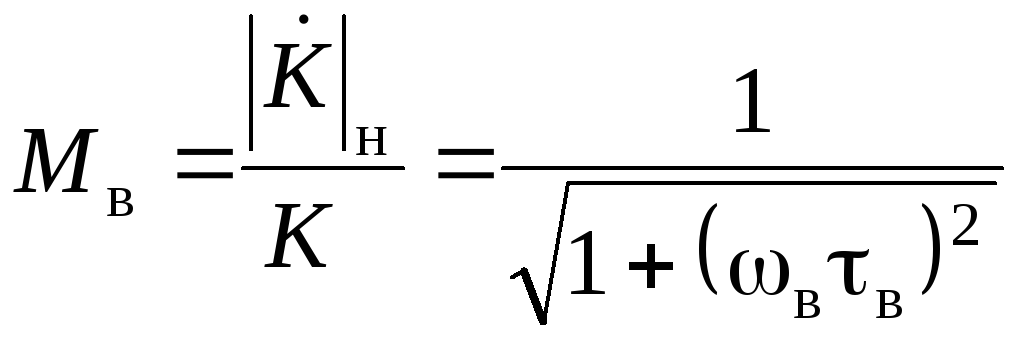. (2.88)

В (2.88) величины М_в и ω_в заданы. Для выполнения заданных условий необходимо выбирать постоянную τ_в из (2.88):

или , (2.89)

где

.

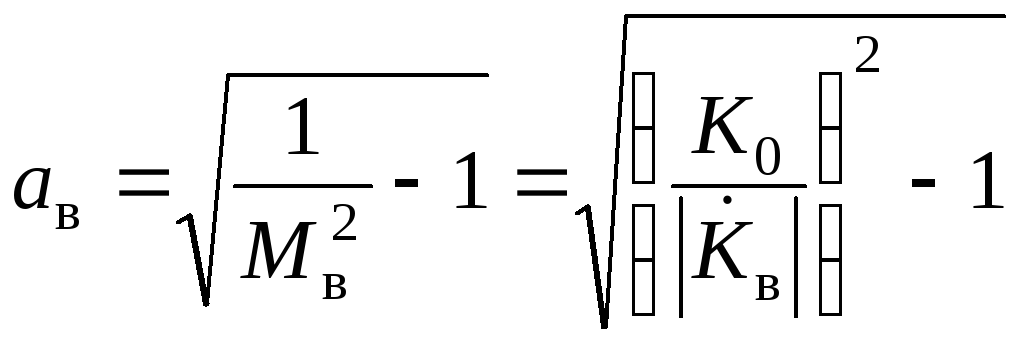Коэффициент а_в и его назначение аналогичны коэффициенту а_н в (2.66) и его назначению (см. подраздел 2.5.3).

Величина τ_в, согласно (2.82), определяется величиной τ_βк из (2.75):

, .

Соотношение между и в (2.75) различно для разных частотных групп транзисторов:

1. Для низкочастотной группы, f_α ≤ 3 МГц,

, .

Граничная частота транзистора f_α должна удовлетворять условию:

.

2. Для среднечастотной группы, 3 МГц < f_α ≤ 30 МГц,

,

можно ввести коэффициент веса k : . Тогда и

.

3. Для высокочастотной группы , f_α > 30 МГц,

, , .

В этой группе для выполнения заданных условий необходимо выбирать низкоомное внешнее сопротивление цепи, что ведет к значительной потери мощности в выходной цепи.

Промежуточный каскад. На выходе этого каскада включена комплексная нагрузка Z_вх.сл, как показано на рис. 2.11,в. Чтобы учесть ее влияние на АЧХ, нужно в (2.81) заменить R'_экв на Z'_экв:

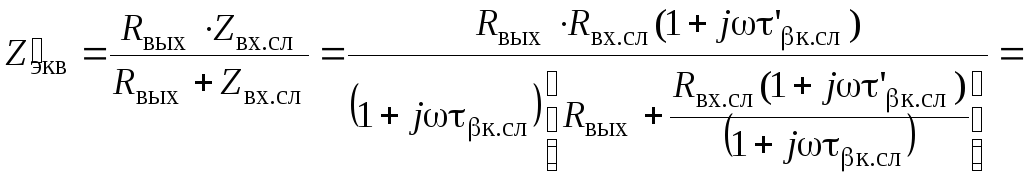
, (2.90)

где Z_вх – из (2.79), индекс _сл – означает «следующий каскад»,

, (2.91)

.

Подставив Z'_экв в (2.81), можно найти

. (2.92)

Выражение (2.92) значительно сложнее (2.81), и полный анализ его в рамках этого курса затруднителен. Однако можно сделать некоторые упрощения. Например, два соседних каскада обычно мало отличаются друг от друга по схеме и по режиму. Можно принять их одинаковыми, тогда

и . (2.93)

На практике часто выполняется условие R_вых >> R_вх.сл., тогда с учетом (2.91)

и анализ (2.93) существенно упрощается:

. (2.94)

Анализ такого промежуточного каскада (при выполнении принятых условий – одинаковые каскады, R_вых >> R_вх.сл) ничем не отличается от анализа одиночного каскада, приведенного ранее. Только постоянная определяется граничной частотой f_{α сл} следующего каскада.