Книги / bobrov_usiliteli / ГЛ2-13

54

2.5.2. Параметры каскада в области средних частот

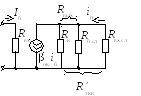
По эквивалентной схеме усилительного каскада для переменных составляющих (см. рис. 2.8,а) легко могут быть определены параметры каскада (, , , ) для средних частот. Они должны быть выражены через элементы схемы (малосигнальные параметры транзистора , , , , резисторы , , , и другие).

Эквивалентный коэффициент _ок. Ток , протекающий во внешней цепи , будет несколько меньше величины , т.к. часть тока ответвляется в параллельную цепь . С учётом сопротивлений параллельных цепей из рис. 2.8,а можно найти

,

где эквивалентное сопротивление внешней цепи, на рис. 2.8,а это – . Для упрощения анализа удобно заменить реальную величину эквивалентной , определённой по отношению к току [1]. Из следует, что

,

где

;

называют коэффициентом токораспределения в коллекторной цепи.

Хотя эквивалентный коэффициент не является параметром только транзистора (учитывается ), он используется часто, при этом уже не приводится на схемах.

Входное сопротивление R_вх. Определяется как сопротивление переменному току между базой транзистора и общим проводом (без учёта делителя , ), как отношение входного напряжения к входному току :

.

Переменное напряжение можно представить как сумму падений напряжений на элементах входной цепи:

.

Подставив в , можно найти

,

где

,

, малосигнальные параметры транзистора (дифференциальное сопротивление эмиттера и объёмное сопротивление базы):

, Ом.

На практике, как правило, имеет место соотношение (, ), что эквивалентно короткому замыканию в выходной цепи по переменному току. Поэтому входное сопротивление

.

Иногда используют другое выражение для входного сопротивления, в которое входит из (2.45) и внешнее сопротивление источника сигнала :

,

где

.

коэффициент токораспределения переменной составляющей в базовой цепи. Коэффициент в является частным случаем при . может состоять из нескольких сопротивлений – и сопротивлений делителя базы (). Для промежуточных каскадов роль играет выходное сопротивление предыдущего каскада (). После того, как определено , эквивалентную схему каскада можно ещё упростить и сделать более удобной и наглядной для определения остальных параметров каскада. Такая «упрощённая» эквивалентная схема каскада приведена на рис. 2.9. Правда, в этой схеме каскада является уже параметром каскада (а не элементом схемы), но вместе с этим мало отличается от четырёхполюсникового параметра транзистора . Поскольку из определяется легко, эквивалентная схема на рис. 2.9 может использоваться с самого начала. Конечно, в «упрощённой» схеме утрачены внутренние связи элементов транзистора , , . Но взаимодействие их учтено в и , во всех остальных параметрах каскада эти элементы так же учитываются через и . В последующих разделах «упрощённая» эквивалентная схема (см. рис. 2.9) будет часто использоваться.

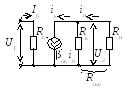
а б

Рис. 2.9

Выходное сопротивление каскада R_вых. Следует заметить, что самостоятельно при анализе используется редко. Оно автоматически входит в выражения других параметров, например коэффициентов усиления. определяется со стороны выходных зажимов при отключенной нагрузке ( на рис. 2.8,а). Все остальные элементы схемы (левее линии а б) входят в , определяемое как отношение переменного напряжения к протекающему под его воздействием току в выходной цепи при отключенной нагрузке и при отсутствии сигнала () на входе:

.

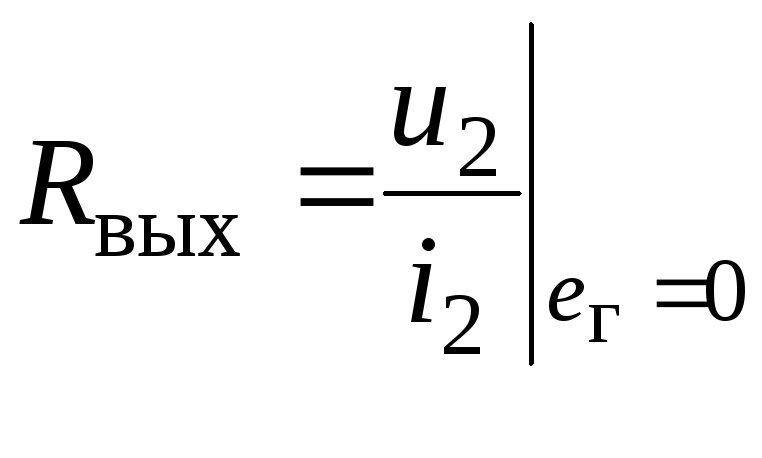Из рис. 2.9,а нетрудно определить, что образуют параллельно включенные и выходное (внутреннее) сопротивление транзистора :

.

При расчётах и анализе учитывают, как правило, приближённое значение :

,

что и отображено на рис. 2.9,а (через (2.43)).

На практике почти всегда выполняется соотношение

,

поэтому на практике часто используют соотношение:

.

Замечание 3. Для нахождения точного значения величина переменного тока (при ) находится аналогично тому, как было найдено приращение тока покоя на рис. 2.7 при нахождении коэффициента нестабильности . А именно, при разомкнутой базе () в выходной (коллекторной) цепи транзистора протекает ток . При замыкании базовой цепи в неё ответвляется (переменный) ток базы и в выходной цепи появляется генератор тока . Искомый ток будет равен разности:

,

по нему и находят :

,

где – обычный (не эквивалентный) коэффициент усиления тока базы; – коэффициент токораспределения в базовой цепи для переменного тока (аналогично для медленных изменений ).

Величина (значит, и ) определяется соотношением сопротивлений в . Возможны два предельных случая:

1. , тогда и . Это возможно при высокоомном делителе , и источнике тока на входе .

2. , тогда и . При этом возможен гипотетический случай , тогда .

Таким образом, точное значение выходного сопротивления транзистора находится в пределах

,

оставаясь всегда больше . Принятая в величина является минимально возможной. Но даже и эта минимальная величина часто не учитывается, т.к. внешне параллельные цепи имеют ещё много меньшее сопротивление, что и учтено в .

Коэффициент усиления напряжения

,

где

– эквивалентное сопротивление всех параллельно включенных сопротивлений в выходной цепи.

Замечание 4. Для предварительного каскада, выход которого подключен ко входу следующего каскада, в изменяется только величина :

.

Иногда полезно представить как . В найдено как произведение тока генератора тока на эквивалентное сопротивление выходной цепи этому току (падение напряжения на ).

Коэффициент усиления тока

.

В – , а определено ранее.

Коэффициент усиления мощности К_р. При необходимости его находят как произведение :

.

Дополнение . Для первого варианта разбиения элементов общей схемы на отдельные каскады (п.2.5.1, замечание 2) параметры по переменному току имеют несколько иной вид. Эти параметры снабжены штрихами.

Входное сопротивление определяется как отношение и и представляет собой сопротивление параллельной цепи из сопротивлений делителя и найденного из (2.45) :

, .

Выходное сопротивление

, (2.58)

будет играть роль для следующего каскада.

Коэффициент усиления напряжения определяется как отношение к ЭДС источника сигнала :

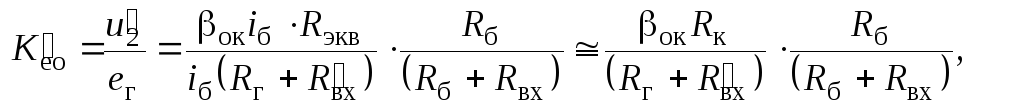(2.59)

где , из ( 2.45), из , .

Для последующих каскадов () сопротивление источника сигнала равно выходному сопротивлению предыдущего ((n – 1)-го) каскада, а ЭДС источника сигнала равна напряжению предыдущего каскада,

, (2.60)

2.5.3. Область низших частот

В области низших частот уменьшается коэффициент усиления, что вытекает из типовой частотной характеристики, показанной на рис. 1.3. Это происходит из-за увеличения сопротивления по переменному току разделительных () и блокирующих () ёмкостей, и эти емкости нужно включать в эквивалентную схему, а коэффициенты усиления надо вычислять с учётом сопротивления этих ёмкостей. Однако одновременный учёт обоих конденсаторов приводит к довольно сложному выражению частотной характеристики, которое весьма затруднительно для анализа. Результирующая низшая граничная частота , обусловленная совместным влиянием ёмкостей , , на уровне 0,7 не имеет достаточно простой связи с низшими граничными частотами , , обусловленными , по отдельности.

Поэтому анализ проводят раздельно для и , а затем результаты объединяют и получают общий результат с некоторой погрешностью.

Влияние разделительных ёмкостей (С_р1). Предположим сначала, что , и выясним роль (). Приведённая запись означает, что величина ёмкости настолько велика, что на низшей граничной частоте , обусловленной только , роль блокирующей ёмкости ещё совсем не проявляется (влияние начинает сказываться на частоте, много меньшей ). При этих условиях оставляем закороченной и в эквивалентную схему не включаем. В эквивалентной схеме, приведённой на рис. 2.10, учитывается только . Кроме того, эта схема составлена для каскада, выход которого подключён ко входу следующего каскада (см. рис. 2.6,б, 2.8,б, 2.9,б), поскольку на практике приходится почти всегда рассматривать именно такую схему. Для схемы на рис.2.6,а в полученных формулах надо принять, .

Рис. 2.10

Коэффициент усиления .

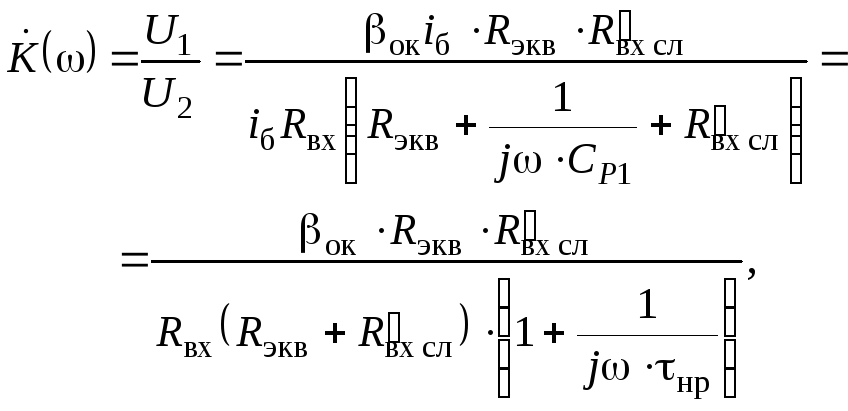
где

, , R_экв = R_к,

.

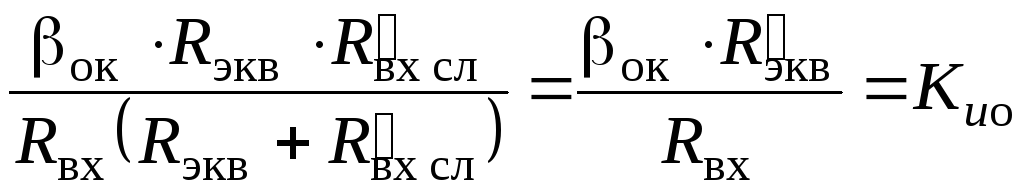В найдено как произведение , а  как часть тока , ответвляющегося в параллельную цепь из , (см. рис. 2.10):

.

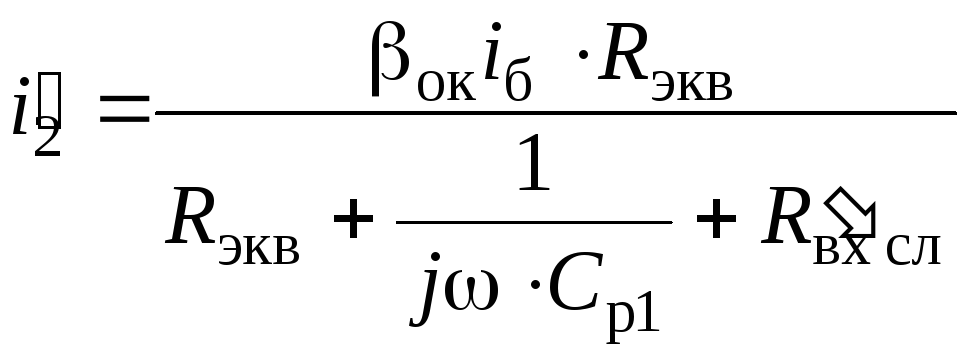С учётом выражение можно представить в удобном для анализа виде:

,

которое включает в себя амплитудно-частотную характеристику (АЧХ) (см. рис. 1.3):

,

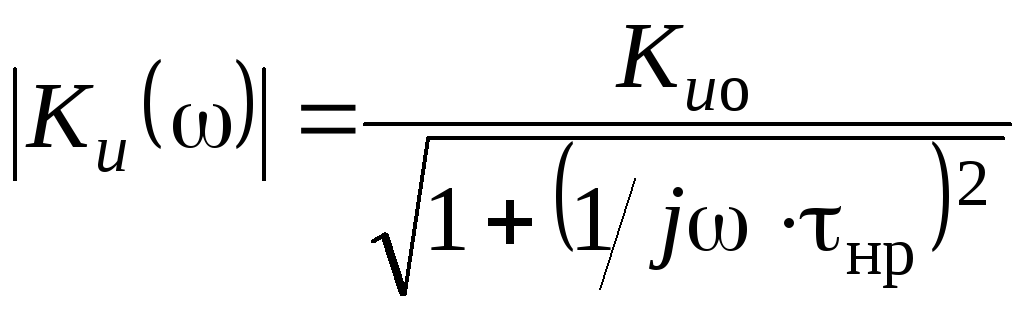и фазочастотную характеристику (ФЧХ) (см. рис. 1.4):

, .

На практике вместо (2.64) чаще используют нормированную АЧХ:

.

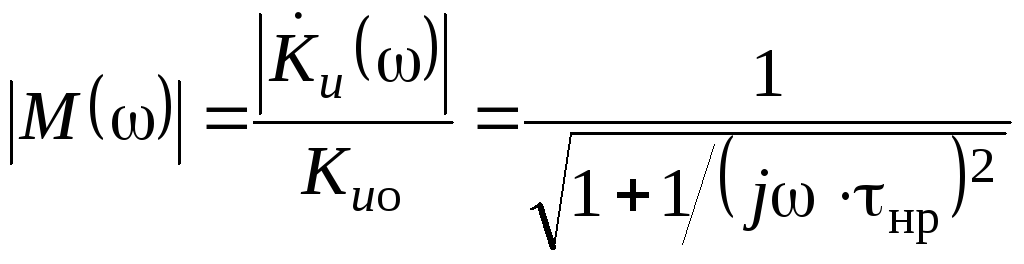Для анализа частотных искажений в УНЧ, как правило, бывает достаточно АЧХ, заданной выражением . Это выражение определяет всю низкочастотную часть АЧХ. Уровень же частотных искажений задаётся одной точкой АЧХ с координатами , :