44

Иногда применяют комбинированную стабилизацию рабочей точки. Ее используют в тех случаях, когда требуется особо высокая степень стабилизации.

2.4.4. Коэффициент нестабильности s

Для количественной оценки стабильности режима покоя и выбора элементов цепей смещения и стабилизации (,,) вводят коэффициент нестабильности [1]

, (2.29)

где – результирующее изменение тока покоя коллектора, обусловленное изменением температуры и действием схемы стабилизации;

–приращение тока в коллекторном переходе, обусловленное изменением температуры и эквивалентное воздействию всех трёх дестабилизирующих факторов, которое можно получить из (2.27), (2.28) и представить в виде

(2.30)

или

где

, (2.31)

, – резисторы делителя на схеме (см. рис. 2.5,б);

, – малосигнальные параметры транзистора.

Первые два слагаемых в (2.30) совпадают с первыми двумя слагаемыми в (2.27), (2.28), поскольку они возникают в коллекторном переходе. Протекая последовательно через эмиттерный переход, эти слагаемые могут существенно увеличиться из-за взаимодействия переходов. Третье слагаемое обусловлено появлением приращения в эмиттерном переходе. В коллекторный переход оно передаётся с коэффициентом . Некоторые исследователи расчёт стабилизации режима покоя ведут раздельно для первых двух слагаемых и для третьего слагаемого в (2.27), (2.28), для чего вводят два коэффициента нестабильности: и [3]. Однако, третье слагаемое в (2.30) можно преобразовать и выделить его эквивалент, аналогичный первым двум по воздействию на конечный результат (приращение ) [1], что значительно проще. В пособии используется второй подход. Формулу (2.25) можно преобразовать:

, (2.32)

где

. (2.33)

Коэффициент называют коэффициентом токораспределения в базовой цепи на ток базы и ток эмиттера . Он будет многократно использоваться при последующем изложении.

Коэффициент в (2.32), как будет показано ниже, как раз и отражает степень увеличения приращений тока, возникающих в коллекторном переходе и протекающих последовательно через эмиттерный переход. Поэтому часть тока из (2.32), равная , может быть представлена в формуле (2.30) как возникающая в коллекторном переходе и может рассматриваться так, как и первые два слагаемых в (2.30).

Если суммарное приращение теплового тока в коллекторном переходе, частично или полностью, протекает через эмиттерный переход (в схеме ОЭ), то в результате взаимодействия p-n переходов часть приращения тока , протекая через эмиттерный переход, увеличивается в раз (аналогично тому, что ). При этом общее приращение коллекторного тока будет больше величины . Степень увеличения (величина ) будет определяться долей , протекающей через эмиттерный переход, а это, в свою очередь, зависит от соотношения сопротивлений в цепи эмиттера и в цепи базы (рис. 2.7). На этом рисунке представлена эквивалентная схема для медленных приращений постоянных токов , , . Она не пригодна для переменных составляющих.

При разомкнутой базовой цепи всё приращение протекает через эмиттерный переход. От взаимодействия p-n переходов приращение тока в коллекторном переходе увеличится в раз, что и отражено генератором тока в выходной цепи . При замыкании базовой цепи в неё будет ответвляться часть тока коллектора , которая

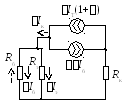
Рис.2.7

будет управлять коллекторным током (изменять его). Этот процесс отражён в выходной цепи генератором тока , который уменьшает общее приращение тока в коллекторной цепи ( направлено навстречу нормальному току базы, отмеченному на рис. 2.7 пунктирной стрелкой). В цепи коллектора установится результирующее приращение (пока неизвестное). Его можно представить как разность токов в выходной коллекторной цепи:

. (2.34)

Величину из схемы на рис. 2.7 можно найти как часть :

(2.35)

где коэффициент токораспределения в базовой цепи, показывающий, какая часть приращения постоянного тока ответвляется в базовую цепь (уже использовался в (2.32) и дан в (2.33)).

Подставив значение в (2.34) и произведя несложные преобразования, а также учтя (2.29), получим

. (2.36)

В теории обратной связи (которая рассматривается в подразделе 2.6) знаменатель из (2.36) называют глубиной обратной связи , а коэффициент коэффициентом обратной связи.

Вернёмся к величине в (2.25) и (2.32). Если третью составляющую в (2.30) умножить на из (2.36), получим исходную величину в (2.25) или в (2.32), что подтверждает правильность объединения всех трёх дестабилизирующих факторов в одной величине в (2.30).

Анализ коэффициента нестабильности S. Из (2.36) следует, что величина определяется величиной , т.е. соотношением сопротивлений и . При изменении от нуля (чистая схема ОЭ, ) до единицы (чистая схема ОБ, ) изменяется в пределах:

(2.37)

Например, если , то и т.е. , что соответствует схеме ОБ (с разомкнутым эмиттером, , ). Это наилучшая стабильность. Наоборот, при , и , что соответствует схеме ОЭ (с разомкнутой базой, , ). Это наихудшая стабильность.

Для получения хорошей стабильности режима покоя необходимо, чтобы величина коэффициента нестабильности была возможно минимальной, т.е. . Для этого необходимо, чтобы , или вытекающее из него условие:

. (2.38)

Условие (2.38) является надёжным ориентиром при проектировании стабильных транзисторных каскадов. Однако достаточно полное его выполнение возможно лишь в микроэлектронных каскадах при использовании специфических методов, например в интегральных дифференциальных усилителях (которые будут подробно рассмотрены позднее). В дискретных транзисторных каскадах выполнить условие (2.38) практически не удаётся. Дело в том, что для выполнения этого условия необходимо увеличивать сопротивление и уменьшать . Однако на то и другое существуют ограничения. Так, уменьшение ведёт к увеличению тока делителя (см. рис. 2.6) и шунтированию входа усилителя . Для хорошей стабильности необходимы соотношения , . И то и другое допустимо в определённых пределах:

(2.39)

Таким образом, на величину существует ограничение снизу.

Увеличение сопротивления ведёт к увеличению напряжения . Но выбирать большую величину (при больших ) нельзя из-за малых допустимых напряжений транзисторов (несколько десятков вольт). Как следует из (2.14), величина ограничена допустимыми напряжениями. На практике величину выбирают в пределах:

(2.40)

или

.

Таким образом, на величину накладывается ограничение сверху.

Практические рекомендации. Практически целесообразно начать расчёт стабильности с выполнения ограничений (2.39) и (2.40). Затем при найденных и вычисляется из (2.36). Если найденная таким образом величина не превышает 4 – 5, то стабильность режима покоя можно считать удовлетворительной. Как правило, при выполнении ограничений стабильность бывает удовлетворительной . При этом соотношение и находится в пределах , что довольно далеко от (2.38). На практике предпочтительнее в (2.39) выбирать величину тока делителя . В этом случае сопротивление делителя находится очень просто:

, , .

Затем определяется из (2.31).